4. Операции над графами

Общепринятыми унарными операциями над графами являются следующие операции:

1. Удаление вершины. Обозначение H=G-v, гдеHиGрезультирующий и исходный графы соответственно,v– удаляемая вершина.

2. Удаление ребра. Обозначение H=G-e, гдеe– удаляемое ребро.

3. Стягивание ребра.

В определённом смысле двойственными к этим операциям являются операции:

4. Добавление вершины. Обозначение H=G+v, гдеv– добавляемая вершина.

5. Добавление ребра. Обозначение H=G+e, гдеe– добавляемое ребро.

6. Расщепление вершины.

Смысл 1,2,4,5 операций очевиден. Рассмотрим подробнее 3 и 6 операции.

Стягивание ребра {u,v} обозначает отождествление смежных вершинu иv.

Для отождествления вершин uиvграфаGнеобходимо выполнить следующие действия:

1. H=G-u-v+v- получить графHпутем удаления из исходного графаGотождествляемых вершинu,vи добавления новой вершиныv.

2. в графе Hсоединить вершинуvребром с каждой вершиной, смежной с вершинойu, а затем с каждой вершиной, смежной с вершинойv, в графеG.

Примеры отождествления вершин и cтягивания ребра представлены на рис. 4.1.

Отметим, что в общем случае при выполнении операции отождествления вершин графа могут образоваться кратные рёбра, то есть результатом такой операции будет мультиграф. Один из таких случаев проиллюстрирован на рис. 4.2.

Пусть v- одна из вершин графаG. Разобьём множество смежных ей вершин (её окружение) на два произвольных подмножестваM иNи выполним следующее преобразование графаG:

1) удалим вершину vвместе с инцидентными ей рёбрами;

2) добавим новые вершины u иwи ребро {u,w};

3) вершину uсоединим ребром с каждой вершиной из множестваM, а вершинуw- с каждой вершиной из множестваN.

Теперь рассмотрим две бинарные графовые операции: объединение и произведения графов.

Граф H=(V,E) называетсяобъединением графовF=(V₁,E₁) иG=(V₂,E₂), еслиV=V₁V₂,E=E₁E₂.

Для обозначения операции объединения графов используется запись H=FG. Пример операции объединения графов показан на рис. 4.3.

Объединение графов F=(V₁,E₁) иG=(V₂,E₂) называетсядизъюнктивным, еслиV₁V₂=.

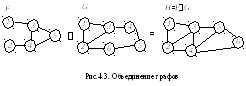
Аналогично определяется объединение и дизъюнктивное объединение любого множества графов, причём в последнем случае никакие два из объединяемых графов не должны иметь общих вершин.

Пусть G_i=(V_i,E_i), (i=1,2) – два графа.Произведением графовG₁G₂называется графG=(V,E), гдеV=V₁V₂– декартово произведение множеств вершин исходных графов, а множествоEформируется по правилу: вершины (u₁,u₂) и (v₁,v₂) смежные в графеGтогда и только тогда, когда илиu₁=v₁, аu₂иv₂смежные вG₂, илиu₂=v₂, аu₁иv₁смежные вG₂(рис. 4.4.)

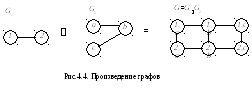
Очевидно, что число вершин графа G=(V,E), полученного в результате произведения графовG₁=(V₁,E₁) иG₂=(V₂,E₂), равно произведению числа вершин графовG₁иG₂, то есть |V|=|V₁||V₂|, а число рёбер определяется так: |E|=|V₁||E₂|+|V₂||E₁|.

С помощью операции произведения вводится понятие n-мерного куба,n-мерный кубQ_nопределяется рекуррентно:

1. Q₁=K₂, гдеK₂– полный граф порядка 2,

2. Q_n=K₂Q_n-1, n>1.

Очевидно, что Q_n– граф порядка 2ⁿ, вершины которого можно представить (0,1)-векторами длиныnтаким образом, что две вершины будут смежные тогда и только тогда, когда соответствующие векторы различаются ровно в одной координате.

Упражнения:

1. Нарисуйте кубы Q₁,Q₂ иQ₃. Определите число рёберn-мерного куба.

2. Постройте алгоритмы, реализующие операции над графами. Какие структуры данных для хранения графов удобнее при реализации тех или иных операций?