3. Некоторые понятия и определения теории графов

В главе 1 мы дали понятие графа. Рассмотрим еще некоторые понятия и определения теории графов.

Отметим, что многие понятия, рассматриваемые в данной главе, не являются устоявшимися, и могут в различной литературе определяться неодинаково.

Пусть v₁,v₂,…,v_n,v_n+1- произвольная последовательность вершин орграфа.

Цепьюназывается любая последовательность дугe₁,e₂,...,e_n, такая, что концевыми вершинами дугиe_iявляются вершиныv_iиv_i+1, то естьe_i=(v_i,v_i+1) илиe_i=(v_i+1,v_i) дляi=1,2,…,n.

Цепь, для которой e_i=(v_i,v_i+1) при всехi=1,2,…,n, называетсяпутём.

Цикломназывается цепь, у которой начальная и конечная вершины совпадают.

Контуромназывается путь, у которого начальная и конечная вершины совпадают.

Цепь, путь, цикл или контур называются простыми, если они не содержат внутри себя циклов.

У графа, изображенного на рис. 3.1

- дуги (v₂,v₁), (v₂,v₂), (v₃,v₂), (v₃,v₄) образуют цепь, соединяющую вершинуv₁с вершинойv₄;

- дуги (v₂,v₂), (v₂,v₄), (v₄,v₃) образуют путь, соединяющий вершиныv₂иv₃;

- дуги (v₃,v₂), (v₂,v₄), (v₃,v₄) образуют цикл с начальной и конечной вершинойv₃;

- дуги (v₃,v₂), (v₂,v₄), (v₄,v₃) образуют контур с начальной и конечной вершинойv₃;

- цепь (v₂,v₁), (v₃,v₂), (v₃,v₄), (v₄,v₃) с начальной вершинойv₁и конечнойv₃не является простой, так как содержит внутри себя цикл (v₃,v₄), (v₄,v₃).

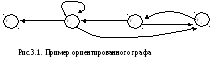
Граф называется связным, если в нем для каждой пары вершин найдётся соединяющая их цепь.

Связный и несвязный граф представлен на рис.3.2.

Любой граф можно рассматривать как некоторую совокупность связных графов. Каждый из этих графов называется компонентомисходного графа.

Несвязный граф, изображённый на рис. 3.2, имеет два компонента.

Множество дуг, исключение которых из графа увеличивает число его компонентов, называется разрезом.

Для связного графа, изображенного на рис. 3.2, разрезом является выделенная дуга e, так как её удаление увеличивает число компонентов до двух.

Пусть G=(V,E),VV,тогда граф, множество вершин которого совпадает сV, а множество дуг включает все дуги множестваEс концевыми вершинами вV, называетсяподграфом графаG,порождённым V.

Пусть EE, тогда граф, для которого множество дуг совпадает сE, а множество вершин включает вершины, инцидентные дугам изE, называетсяподграфом графаG,порождённым E.

Граф называется полным, если любые две его вершины смежные.

Граф Gназываетсяпустым, если в нём нет рёбер.

Граф, который не содержит циклов, называется ациклическим.

Связный неориентированный ациклический граф называется деревом, множество деревьев называетсялесом.

Если рёбра, составляющие дерево, заменить ориентированными дугами, то получим ориентированное дерево. Если из контекста ясно, о каком дереве идет речь, то в дальнейшем слово «ориентированное» будем опускать.

Для ориентированного дерева имеет смысл ввести понятие корня. Минимальное по мощности множество вершин ориентированного дерева, из которых существуют пути во все оставшиеся вершины, будем называть множеством корней.

Покрывающим (остовным) деревомграфаG называется дерево, являющееся подграфом графаGи содержащее все его вершины.

Если граф Gнесвязен, то множество, состоящее из основных деревьев каждой компоненты, называетсяпокрывающим (остовным) лесом.

Обобщением графа является гиперграф.

В гиперграфе, в отличие от графа, рёбрами могут быть не только двухэлементные, но и любые подмножества вершин.

Подобные объекты в математике известны давно, однако введение термина “гиперграф” связано с успешным рассмотрением на них ряда важных понятий и методов теории графов.

Упражнения:

1.Определить число рёбер в полном графе порядка n. Нарисовать примеры полных графов порядка 2, 3, 4, 5.

2.Определить число рёбер в покрывающем дереве графа порядка n.