7.1. Условия существования потока

Пусть задан граф G=(V,E), каждой дуге (x,y)Eприписано два числаf(x,y) иc(x,y) – число единиц потока, проходящих по дуге (x,y), и пропускная способность дуги (x,y) соответственно. Пусть в графеGтакже выделено две вершиныsV– источник иtV– сток. Если при этом выполняются следующие условия:

1) (x,y)E; 0f(x,y)c(x,y) (7.1)

2) xV, xs, xt;  f(x,y)- f(y,x) = 0 (7.2)

yV yV

3)  f(s,y) -  f(y,s) = v (7.3)

yV yV

4)  f(y,t) -  f(t,y) = v (7.4)

yV yV

то говорят, что в графе G задан поток величины v (из источника в сток передается v единиц потока).

Первое условие для каждой дуги (x,y) ограничивает число единиц потока, проходящих по дуге (x,y), пропускной способностью этой дуги.

Второе условие запрещает утечки потока в промежуточных вершинах (в вершинах, отличных от источника и стока), то есть для каждой промежуточной вершины число приходящих единиц потока в эту вершину должно быть равно числу единиц потока, выходящих из неё.

Третье и четвертое условие задает баланс единиц потока, выходящих из источника и приходящих в сток: сколько единиц потока вышло из источника, столько же единиц потока должно прийти в сток.

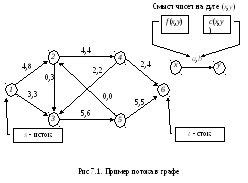
Пример графа с заданным потоком величины 7 представлен на рис.7.1.

7.2. Поиск увеличивающей цепи

Пусть задан граф G=(V,E), в котором существует некоторый поток из вершины s в вершину t. Требуется ответить на вопрос: можно ли увеличить поток из s в t?

Цепь, по которой могут быть посланы дополнительные единицы потока, называется увеличивающей цепью.

Алгоритм 5. Алгоритм поиска увеличивающей цепи

Шаг 1. Разбить множество дуг графа G=(V,E) на группы:

Группа N – дуги графа, в которых поток не может изменяться (дуги с нулевой пропускной способностью или дуги, в которых по каким-либо причинам, например, техническим, число проходящих единиц потока должно быть постоянным).

Группа I – дуги, в которых поток может увеличиваться, то есть дуги (x,y), в которых число проходящих единиц потока f(x,y) меньше пропускной способности c(x,y).

Группа R – дуги, в которых поток может уменьшаться, то есть дуги (x,y), в которых число проходящих единиц потока f(x,y) больше нуля.

Шаг 2. Дуги множества N из дальнейшего рассмотрения исключить. Окрасить вершину s.

Шаг 3. Окрашивать дуги и вершины в соответствии с приводимыми ниже правилами до тех пор, пока либо не будет окрашена вершина t, либо окраска новых вершин и дуг станет невозможной.

Правила окрашивания вершины y и дуг (x,y),(y,x) при уже окрашенной вершине x:

1. если (x,y)I, то окрашивается вершина y и дуга (x,y);

2. если (y,x)R, то окрашивается вершина y и дуга (y,x);

3. в противном случае окрашивание вершины y и дуги (x,y) не производится.

Если дуга окрашивается по первому правилу, то она называется прямой дугой. Если дуга окрашивается по второму правилу, то она называется обратной дугой.

Шаг 4. Если вершина t окрашена, то выбрать окрашенные дуги, образующие цепь, соединяющую вершины s и t. Такая цепь является увеличивающей. В противном случае увеличивающей цепи в графе нет.

Для графа, изображенного на рис.7.1, выполнение первого шага алгоритма даст следующее разбиение дуг графа на группы N,I,R: N={(5,2)}, I={(1,2), (2,3), (3,5), (4,6)}, R={(1,2), (1,3), (2,4), (3,5), (4,3), (4,6), (5,6)}. После выполнения третьего шага алгоритма будут окрашены следующие дуги (1,2), (2,3), (3,5), (4,3), (4,6), см. рис. 7.2. После выполнения четвертого шага алгоритма получим увеличивающую цепь =(V,E), V={1,2,3,4,6}, E={(1,2), (2,3), (4,3), (4,6)}.

После того, как увеличивающая цепь =(V,E) найдена, производится увеличение потока вдоль найденной цепи по правилам:

1. Находится величина

t = min {(a,b)}

(a,b)E

Смысл чисел (a,b) зависит от того, какой дугой – прямой или обратной – является дуга (a,b). Для прямых дуг (a,b) – максимальная величина, на которую может быть увеличен поток по дуге (a,b), то есть (a,b)=c(a,b)-f(a,b). Для обратных дуг (a,b) – максимальная величина, на которую может быть уменьшен поток по дуге (a,b), то есть (a,b)=f(a,b).

2. В каждой прямой дуге (a,b)E число проходящих единиц потока f(a,b) увеличивается на t единиц. В каждой обратной дуге (a,b)E число проходящих единиц потока f(a,b) уменьшается на t единиц. В результате таких действий суммарный поток в графе увеличивается на t единиц.

Увеличим поток в графе, изображенном на рис.7.1, вдоль увеличивающей цепи =(V,E), см. рис.7.2.

1. t=min{c(1,2)-f(1,2), c(2,3)-f(2,3), f(4,3), c(4,6)-f(4,6)}=

min{8-4,3-0,2,3-1}=2.

2. f(1,2) = f(1,2)+t = 4+2 = 6, f(2,3) = f(2,3)+t = 0+2 = 2,

f(4,3) = f(4,3)-t = 2-2 = 0, f(4,6) = f(4,6)+t = 2+2 = 4.

Увеличенный таким образом поток показан на рис. 7.3. В обратной дуге (4,3) поток уменьшается на две единицы, эти две единицы возвращаются по прямой дуге (4,6) в сток, а соответствующая нехватка потока в вершине 3 компенсируется за счет двух единиц, поступающих по прямым дугам (1,2) и (2,3). Таким образом, суммарный поток из источника в сток увеличился на 2 единицы.