А) последовательное;б) параллельное;в) отрицательная обратная связь

Последовательное соединение двух звеньев W₁(p) и W₂(p) (Рисунок 2 .9 – Виды соединений звеньев в структурной схем а) можно заменить одним звеном W (p) = W₁(p)W₂(p). Параллельное соединение (Рисунок 2 .9 – Виды соединений звеньев в структурной схем б) – звеном W (p) = W₁(p) + W₂(p). Отрицательную обратную связь (Рисунок 2 .9 – Виды соединений звеньев в структурной схем в) – звеном:

.

(2.13)

Алгоритм поиска передаточной функции для произвольной структурной схемы:

1. Сформировать систему уравнений структурной схемы.

   1. Пометить все связи, соединяющие компоненты произвольными переменными.

   2. Для каждого компонента записать уравнение модели.

2. Исключить все переменные из системы уравнений кроме переменных, обозначающих вход и выход системы.

3. Конец.

Пример 2.5

Вычислить передаточную функцию для обратной связи (Рисунок 2 .9 – Виды соединений звеньев в структурной схеме в).

Решение.

Связи, соединяющие узел со звеньями² W₁ и W₂ можно сразу пометить переменной Y, это соответствует модели узла заданной уравнением ( 2 .7). Все остальные связи на Рисунок 2 .9 – Виды соединений звеньев в структурной схеме в помечены. Запишем уравнение для сумматора, или точнее говоря для элемента сравнения, так как один из его входов помечен знаком минус: X₁=X-X₂. Уравнение для звена W₁: Y=W₁X­₁, для W₂: X­₂=W₂Y. В итоге получаем систему уравнений:

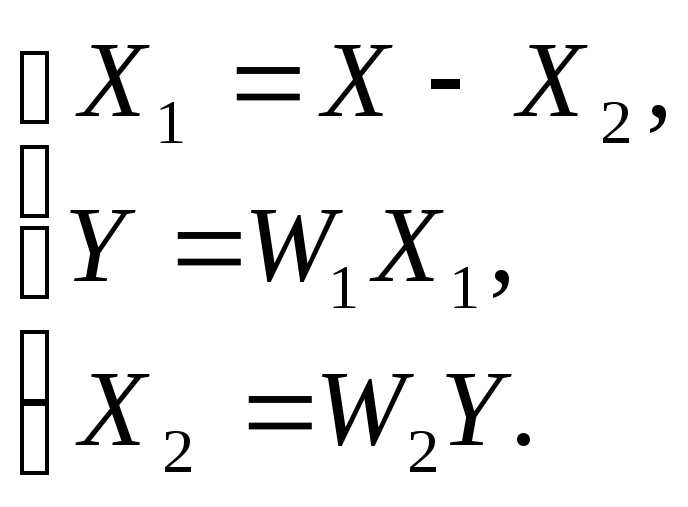
Исключим X₂, а затем X₁:

.

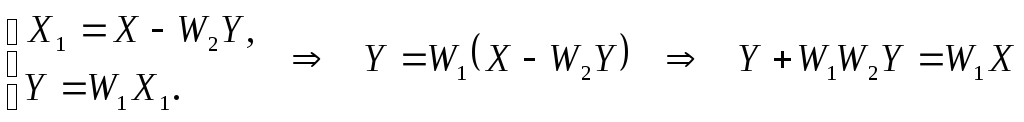Получаем передаточную функцию, совпадающую с выражением ( 2 .13): , т.е..

Варианты заданий.

2.3. Характеристики линейных систем автоматического управления

Заменив в передаточной функции W(p) аргумент p на j получим частотную характеристику W(j), где j – мнимая единица,  – циклическая частота входного гармонического сигнала. Частотную характеристику можно записать двумя способами, в алгебраической форме ( 2 .14) и экспоненциальной форме ( 2 .15).

, ,	(2.14) (2.15)

где U() – действительная часть или вещественная частотная характеристика (ВЧХ), V() – мнимая часть, A() – амплитудно-частотная характеристика, () – фазо-частотная характеристика.

Амплитудно-частотная характеристика (АЧХ) показывает зависимость амплитуды выходного сигнала от частоты входного гармонического сигнала единичной амплитуды. Фазо-частотная характеристика (ФЧХ) показывает зависимость фазы выходного сигнала от частоты входного сигнала с нулевой фазой. Таким образом, если на входе системы действует сигнал x(t)=sin(t), то на выходе системы будет сигнал y(t)=A()sin(t+ ()).

Связь между АЧХ, ФЧХ и действительной и мнимой частями осуществляется по формулам Эйлера³:

, ,	(2.16) (2.17)

где .

, .	(2.18) (2.19)

Кроме вышеперечисленных характеристик, применяют также следующие: логарифмическая амплитудно-частотная характеристика (ЛАЧХ); амплитудно-фазовая характеристика (АФХ). ЛАЧХ находится по формуле ( 2 .20).

(2.20)

АФХ задается двумя характеристиками как параметрическая функция, зависящая от частоты. График АФХ (годограф) строится при изменении частоты  от 0 до , причем существует два способа: 1) если АФХ задан характеристиками АЧХ и ФЧХ, тогда годограф строится в полярных координатах, 2) если АФХ задан характеристиками U() и V(), тогда годограф строится в декартовых координатах (Рисунок 2 .10 – Пример построения годографа АФХ).

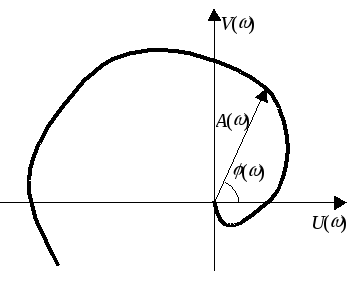
Рисунок 2.10 – Пример построения годографа АФХ

Пример 2.6

Найти частотные характеристики для системы с передаточной функцией .

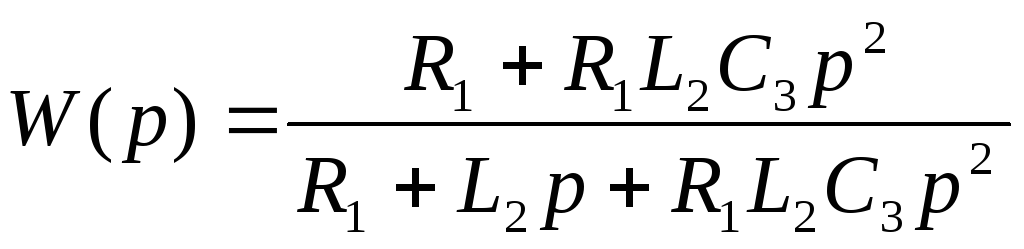Решение.

Заменим в данной передаточной функции параметр p на j и получим частотную характеристику:

.

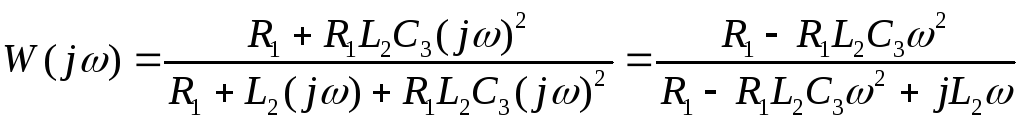Для того чтобы выделить действительную и мнимую части из частотной характеристики домножим числитель и знаменатель на комплексно-сопряженное выражение знаменателя:

,

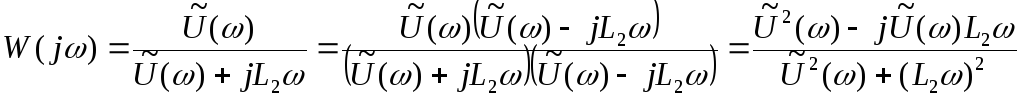где .

Разделив почленно действительную и мнимую части на знаменатель и сопоставив результат с ( 2 .14) получим:

.

ФЧХ находится по формуле ( 2 .17), где

.
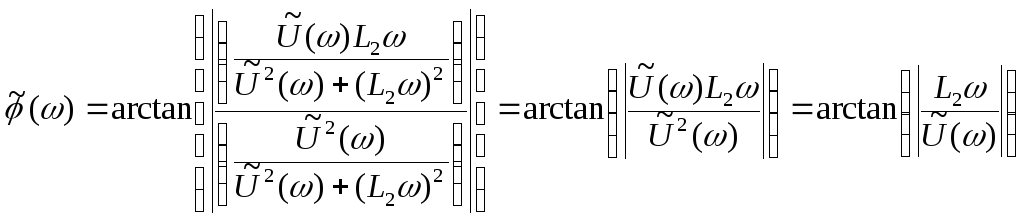
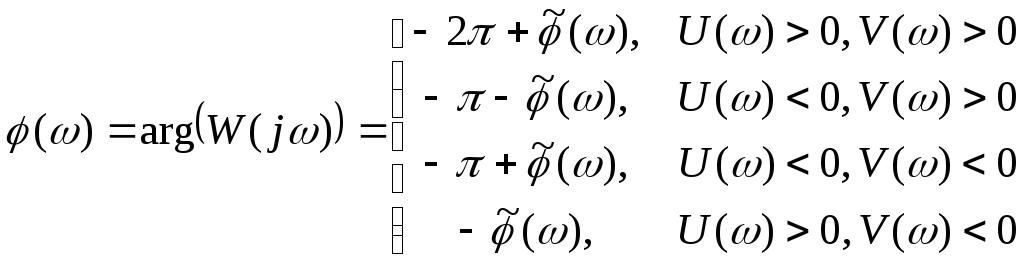