2.3. Устойчивость линейных систем автоматического управления

Критерии устойчивости разделяют на алгебраические и графоаналитические.

Алгебраические.

Передаточную функцию системы записывают в дробно-рациональном виде:

,

(2.21)

причем таким образом, чтобы выполнялось условие a₀>0.

Корневой критерий.

Решается характеристическое уравнение: , гдеQ(p) – знаменатель передаточной функции ( 2 .21) (характеристический полином).

Система устойчива, если все корни характеристического уравнения (полюса) лежат в левой полуплоскости, т.е. Re(p_i)<0, i=1,...,n (Рисунок 2 .11 – Пример определения устойчивости по корневому критерию).

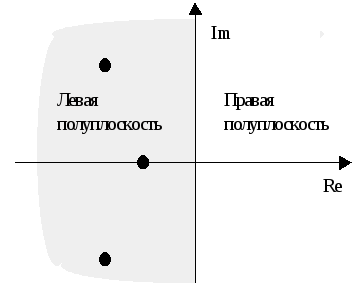
Рисунок 2.11 – Пример определения устойчивости по корневому критерию

Критерий Рауса-Гурвица.

Из коэффициентов полинома Q(p) составляют таблицу C_i,j, где i – номер столбца, j – номер строки. Первую строку таблицы (элементы C_i,1) составляют из коэффициентов с четными индексами: a₀, a₂, ... . Вторую строку таблицы (элементы C_i,2) составляют из коэффициентов с нечетными индексами: a₁, a₃, ... . Остальные элементы таблицы вычисляют по рекуррентной формуле:

,.

(2.22)

где – коэффициент, вычисляющийся для каждойj-й строки отдельно.

Для простоты восприятия рекуррентной формулы ( 2 .22) можно воспользоваться образом изображенным на Рисунок 2 .12 – Пояснение к рекуррентной формуле, т.е. чтобы найти некоторый элемент таблицы, надо взять элементы двух предыдущих строк. Для вычисления коэффициента r берутся элементы из первого столбца таблицы, а элементы из столбца, справа от искомого, помещаются в первый столбец определителя.

Критерий Рауса-Гурвица заключается в следующем: система устойчива, если все n+1 элементов первого столбца таблицы будут положительными, т.е. , гдеn – степень полинома Q(p) (порядок системы).

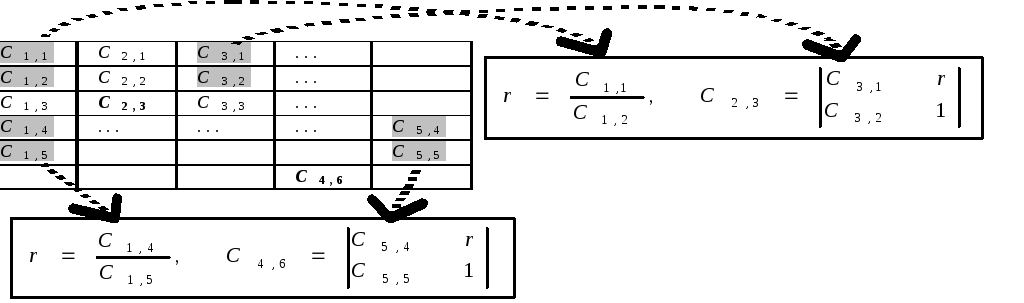
Рисунок 2.12 – Пояснение к рекуррентной формуле

Критерий Гурвица.

Передаточная функция берется в том же виде ( 2 .21). Составляется определитель порядка n следующим образом: первая строка составляется из коэффициентов с нечетными степенями: a₁, a₃, ... , вторая строка – из коэффициентов с четными степенями: a₀, a₂, ... . Остальные строки составляются аналогичным образом, со сдвигом коэффициентов вправо на одну позицию (Рисунок 2 .13 – Определитель Гурвица).

Критерий Гурвица заключается в следующем: система устойчива, если все диагональные миноры больше нуля, т.е. .

Рисунок 2.13 – Определитель Гурвица

Диагональные миноры находятся следующим образом:

.

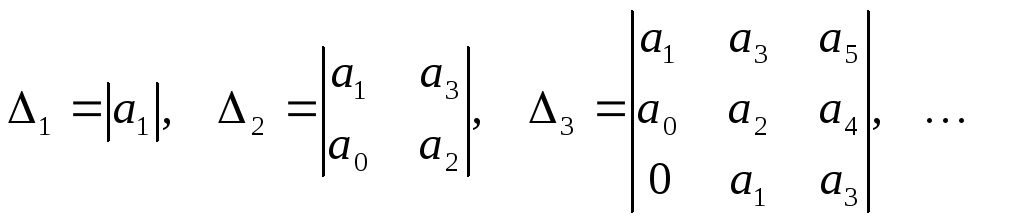Пример 2.7

Определить устойчивость системы корневым критерием, критерием Рауса-Гурвица и критерием Гурвица.

Решение.

Найдем корни характеристического уравнения . Данное уравнение можно решить через дискриминант:, тогда. Корни лежат в левой полуплоскости, следовательно, система устойчивая.

Определим устойчивость системы по критерию Рауса-Гурвица. Коэффициенты характеристического полинома следующие: . Составим таблицу Рауса-Гурвица:

j \ i	1	2
1	0,08	1
2	0,3	0
3	1	...

Найдем элемент C_1,3 таблицы Рауса-Гурвица, для этого используем уже имеющиеся элементы таблицы (помечены маркером):

.

Все три элемента первого столбца таблицы найдены, следовательно, дальнейшее заполнение таблицы не имеет смысла. Данная система устойчива, так как все (n+1) элементов первого столбца больше нуля, .

По определителю Гурвица порядка n=2 , получаем:и. Система устойчива, так как.

Графоаналитические.

Критерий Михайлова.

В полиноме Q(p) ( 2 .21) параметр p заменяем на j, для полученной функции Q(j) строим годограф, подобно тому, как для W(j) строим годограф АФХ. Система устойчива, если годограф начинается на положительной действительной полуоси, и, огибая начало координат против часовой стрелки, проходит n квадратов, где n – порядок системы (Рисунок 2 .14 – Пример годографа Михайлова устойчивой системы 5-ого порядка).

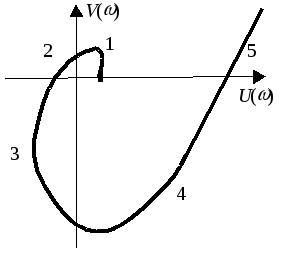
Рисунок 2.14 – Пример годографа Михайлова устойчивой системы 5-ого порядка

Критерий Найквиста.

С помощью данного критерия определяют устойчивость замкнутой системы по признакам разомкнутой системы (Рисунок 2 .15 – К понятию замкнутой и разомкнутой системы).

Рисунок 2.15 – К понятию замкнутой и разомкнутой системы

а) замкнутая;б) разомкнутая

Критерий заключается в следующем: замкнутая система устойчива, если АФХ разомкнутой системы огибает точку (-1; j0) на угол k , где k – количество полюсов разомкнутой системы, находящейся в правой полуплоскости. Фраза «АФХ огибает точку (-1; j0) на угол k» означает следующее: вектор Ф(j) проведенный из точки (-1; j0) к точке годографа АФХ поворачивается на угол k при изменении  от 0 до  (Рисунок 2 .16 – АФХ разомкнутой системы).

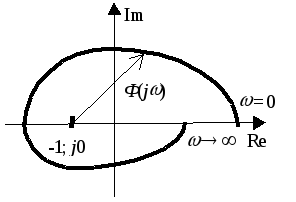
Рисунок 2.16 – АФХ разомкнутой системы

Логарифмический критерий Найквиста.

Замкнутая система будет устойчива, если график ЛАЧХ разомкнутой системы пересечет уровень 0 раньше, чем ФЧХ разомкнутой системы окончательно пересечет сверху вниз уровень -. На Рисунок 2 .17 – ЛАЧХ и ФЧХ разомкнутой системы изображены примеры ЛАЧХ и ФЧХ разомкнутой системы для неустойчивой замкнутой системы (график ФЧХ –  ₁()) и устойчивой замкнутой системы (ФЧХ –  ₂()).

Рисунок 2.17 – ЛАЧХ и ФЧХ разомкнутой системы