1.4. Повторные независимые

испытания

В теме изучаются методы решения задачи, в которой один и тот же опыт повторяется несколько раз. В результате каждого опыта может появиться или не появиться интересующее нас событие. Однако нас интересует не результат отдельного опыта, а результат серии опытов, т. е. какова вероятность появления того или иного числа событий в серии опытов. Характерным примером такой задачи являются различного рода выборки. Когда образована выборка и произ­водится ее изучение, то каждый элемент ее обследуется и устанавливается на­личие или отсутствие того или иного фактора. Обследование одного элемента выборки и есть опыт или испытание. Обследование всех элементов выборки, про­водимое в одинаковых условиях, есть повторение испытаний, рассматриваемое в задаче о повторении опытов.

Формула Пуассона наряду с задачей повторения испытаний используется также для расчета вероятности появления различного числа событий (например, точек или других элементов) в какой-либо области (площади, объеме или во времени). При этом должны соблюдаться следующие условия: события (точки) в области распределены в общем равномерно;положение каждого события (точки) случайное, независимое друг от друга;события (точки) появляются в области поодиночке, а не парами, тройками и т. д.

При решении задач с использова­нием формулы Пуассона исходные данные могут встречаться в двух вариантах:

1) в условии задачи указывается вероятность р появления события в одном испытании и число испытаний n;

2) в условии задачи указывается среднее число появлений события за какую-либо единицу области (площади, объема, времени) и размер области s {площади, объема, времени), внутри которой появляются интересующие события.

В первом случае параметр распределения Пуассона определяется как про­изведение вероятности р и числа п испытаний: = пр.

Во втором случае этот параметр определяется произведением среднего чис­ла появлений события и размера области: .

Дальнейший расчет вероятности по формуле Пуассона одинаков в обоих случаях.

1. Формула Бернулли. Рассмотрим случай, когда требуется определить не вероятность осуществления некоторого события в одном испытании, а вероятность того, что это событие произойдет заданное количество раз в серии из опытов. Будем считать при этом, что вероятность в каждом опыте одинакова и результат каждого опыта не зависит от результатов остальных. Такая постановка задачи называется схемой независимых испытаний. При выполнении указанных условий вероятность того, что при проведении независимых испытаний событие будет наблюдаться ровно раз (неважно, в каких именно опытах), определяется по формуле Бернулли:

где — вероятность появления в каждом испытании, а — вероятность того, что в данном опыте событие не произошло.

В частности, отсюда Р_n(0)=qⁿ, Р_n(1)=npq^n-1, … , Р_n(n)=pⁿ.

Примеры.

1. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.

Событие А – достали белый шар. Тогда вероятности , . По формуле Бернулли требуемая вероятность

. ◄

2. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.

Вероятность рождения девочки , тогда .

Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:

, ,

, .

Следовательно, искомая вероятность

. ◄

3. Правильная игральная кость бросается четыре раза. Найти вероятность того, что шесть очков выпадут ровно два раза.

Обозначим {выпадение на одной кости шести очков}. Очевидно, что в этом случае испытания независимы, и мы имеем схему Бернулли с , , а так как кость правильная . Вычислим

.

Подставляя эти значения в формулу Бернулли, получим искомую вероятность

. ◄

4. Вероятность появления события в каждом из 5 независимых испытаний равна 0.8 . Найти вероятность того, что событие А произойдет

а) не менее трех раз б) не более двух раз.

Имеем ,

Подставляя эти значения в формулу для , получим

а)

.

б)

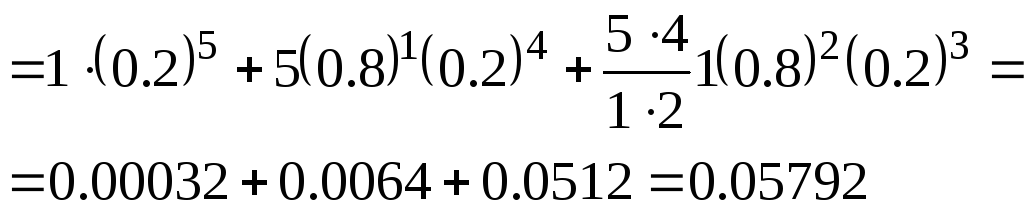
Нетрудно видеть, что событие а) = { не менее двух попаданий при шести выстрелах, т.е. 2, 3, 4, 5, 6 попаданий} и событие б) ={не более одного попадания при шести выстрелах, т.е. 0 и 1 попадание } составляют полную группу событий с суммой вероятностей равной 1, . Поэтому вероятность события б) можно подсчитать, используя значение , полученное в а) . ◄

■▬▬▬►

2. Число наступлений события называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления любое другое количество раз.

Наивероятнейшее число наступлений события в испытаниях заключено между числами и .

Замечание. Если – целое число, то наивероятнейших чисел два: и .

Пример. Вероятность попадания в цель при каждом выстреле из лука равна 1/3. Производится шесть выстрелов. Какова вероятность ровно двух попаданий? Какова вероятность не менее двух попаданий? Каково наивероятнейшее число попаданий?

Обозначим A = {попадание при одном выстреле} p = 1/3, q = 1 – 1/3 = 2/3. Число выстрелов n = 6. Естественно предположить, что выстрелы не зависят друг от друга, и мы имеем схему Бернулли.

Ответ на первый вопрос находим по формуле Бернулли, n = 4, m =2

.

Ответ на второй вопрос можно найти по формуле для . Однако проще найти по этой формуле, вероятность не более одного попадания и вычесть эту вероятность из 1.

.

В этом рассуждении мы использовали тот факт, что событие B₁ = { не менее двух попаданий при шести выстрелах, т.е. 2, 3, 4, 5, 6 попаданий} и событие B₂= { не более одного попадания при шести выстрелах, т.е. 0 и 1 попадание } составляют полную группу событий с суммой вероятностей равной 1. Для ответа на третий вопрос найдем

, ,

следовательно, наивероятнейшее число попаданий, лежащее между этими числами, равно двум. ◄

◄▬▬▬■

3. Формула Пуассона. При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например, 0,95¹⁰⁰⁰ вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз используют формулу Пуассона

,

где λ=np=const – среднее число появлений события в n испытаниях.

Примеры.

1. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

N=1000, p=0,002, λ=np=2, k=3.

Искомая вероятность

. ◄

2. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.

n=500, p=0,004, λ=2.

По теореме сложения вероятностей

. ◄

3. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.

λ=np=1000·0,003=3

.

◄

4. Радиоаппаратура состоит из 2000 элементов. Вероятность отказа одного элемента в течение года равна 0,001 . Какова вероятность отказа двух элементов за год? Какова вероятность отказа не менее двух элементов за год?

Работу каждого элемента рассматриваем как отдельное испытание. Обозначим А = { отказ элемента за год }. Имеем n = 2000, p = p(А) = 0.001, λ = n p = 2000∙0,001 = 2. По формуле Пуассона

.

Ответ на второй вопрос дается формулой

. ◄