II. Случайные величины и их

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

Понятие случайной величины — основное в теории вероятностей. Примене­ние теории вероятностей для решения практических задач в первую очередь связано с этим понятием. Следует хорошо разобрать методику задания случай­ной величины дискретного типа с помощью таблицы или многоугольника распре­деления, а непрерывного типа — с помощью дифференциальной функции или кри­вой распределения, использование этих понятий для расчета вероятности попада­ния случайной величины в заданный интервал. Далее необходимо усвоить поня­тия математического ожидания и дисперсии как числовых характеристик наибо­лее важных свойств случайной величины.

Во многих задачах теории вероятности удобнее оперировать не понятием случайного события, для которого существуют только две возможности: оно может произойти или не произойти в результате опыта, а понятием так называемой случайной величины, то есть величины, которая при проведенном испытании может принимать различные значения, причем заранее не известно, какие именно. Если возможный диапазон значений такой величины представляет собой конечное или счетное множество, она называется дискретной случайной величиной, а если эти значения заполняют целиком некоторый интервал — непрерывной случайной величиной.

2.1. Дискретные случайные величины

1. Поведение дискретной случайной величины описывается законом распределения (или рядом распределения) — таблицей, в первой строке которой перечислены все возможные значения случайной величины, а во второй — вероятности, с которыми она принимает эти значения:

Сумма вероятностей должна при этом равняться числу 1.

Пример. Из партии, содержащей 10 деталей, среди которых две бракованных, взяты наудачу три детали. Составить ряд распределения случайной величины — числа стандартных деталей среди отобранных.

Так как бракованных деталей в партии только две, среди трех отобранных должна быть, по крайней мере, одна стандартная деталь. Следовательно, случайная величина может принимать три значения: Найдем соответствующие им вероятности. Число возможных наборов по три детали из 10 имеющихся, то есть число возможных исходов опыта, составляет

Найдем число исходов, благоприятствующих каждому значению случайной величины:

Тогда Поэтому ряд распределения имеет вид:

◄

Пример. В магазине куплено 3 электроприбора: чайник, утюг и пылесос. Вероятность выхода из строя в течение гарантийного срока для каждого из них соответственно равна р₁=0,05, р₂=0,1, р₃ = 0,2. Составить закон распределения случайной величины Х – числа приборов, вышедших из строя в течение гарантийного срока.

Х – число приборов, вышедших из строя, имеет следующие возможные значения: х₁=0 – все три прибора не выйдут из строя в течение гарантийного срока;

х₂=1 – один прибор выйдет из строя; х₃=2 – два прибора выйдут из строя;

х₄=3 – три прибора выйдут из строя.

Найдем соответствующие этим значениям вероятности. По условию вероятности выхода из строя приборов равны:

р₁=0,05; р₂=0,1; р₃=0,2, тогда вероятности того, что приборы будут рабочими в течение гарантийного срока равны:

q₁ = 1 – p₁ = 1 – 0,05 = 0,95; q₂ = 1 – p₂ = 1 – 0,1 = 0,9; q₃ = 1 – p₃ = 1 – 0,2 = 0,8.

P₁ (X=0) = q₁ ∙ q₂ ∙ q₃ = 0,95 ∙ 0,9 ∙ 0,8 = 0,684.

P₂ (X=1) = q₁ ∙ q₂ ∙ p₃ + q₁ ∙ p₂ ∙ q₃ + p₁ ∙ q₂ ∙ q₃ = 0,95 ∙ 0,9 ∙ 0,2 + 0,95 ∙ 0,1 ∙ 0,8 + 0,05 ∙ 0,9 ∙ 0,8 = 0,283.

P₃ (X=2) = p₁ ∙ p₂ ∙ q₃ + p₁ ∙ q₂ ∙ p₃ + q₁ ∙ p₂ ∙ p₃ = 0,05 ∙ 0,1 ∙ 0,8 + 0,05 ∙ 0,9 0,2 + 0,95 ∙ 0,1 ∙ 0,2 = 0,032.

P₄ (X=3) = p₁ ∙ p₂ ∙ p₃ = 0,05 ∙ 0,1 ∙ 0,2 = 0,001.

Проверка: P=P₁(X=0)+P₂(X=1)+P₃(X=2)+P₄(X=3)=0,684+0,283+0,032+0,001=1.

Закон распределения имеет вид:

X	0	1	2	3
p	0,684	0,283	0,032	0,001

◄

Пример. На сборку поступило 30 деталей, из них 25 стандартных. Сборщик берёт наудачу 3 детали. Составить закон распределения случайной величины Х – числа стандартных деталей среди трёх отобранных.

Возможные значения случайной величины Х: Х₁ = 0, Х₂ = 1, Х₃ = 2, Х₄ = 3. Вероятности этих значений вычисляются по формуле Р_n(Х=m) = ,

где n – число элементов множества, s – число элементов множества, обладающих фиксированным свойством; r – число отобранных элементов; m= - число элементов с фиксированным свойством, оказавшихся в выборке. Такое распределение называют гипергеометрическим.

P₃(X=0) = 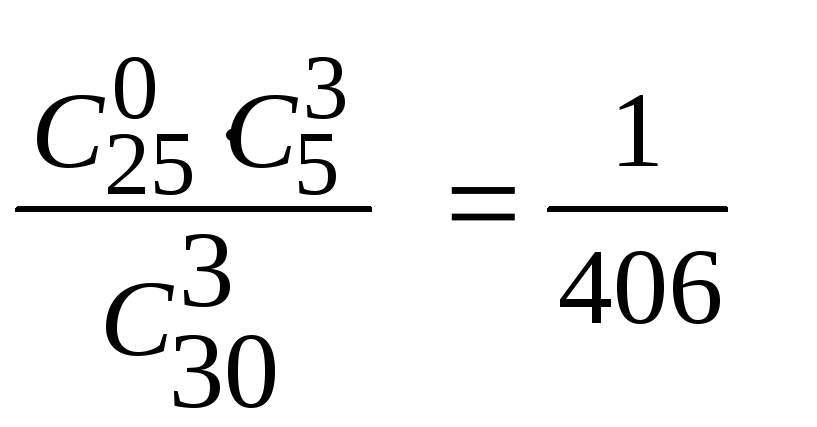. P₃(X=1) = .

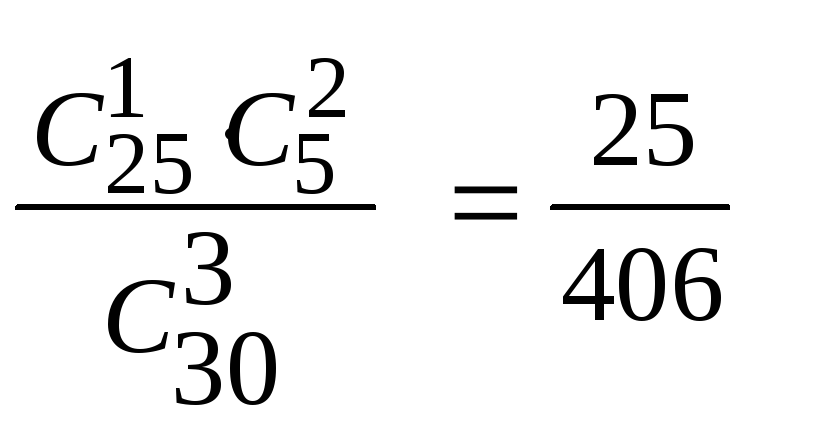P₃(X=2) = . P₃(X=3) = .

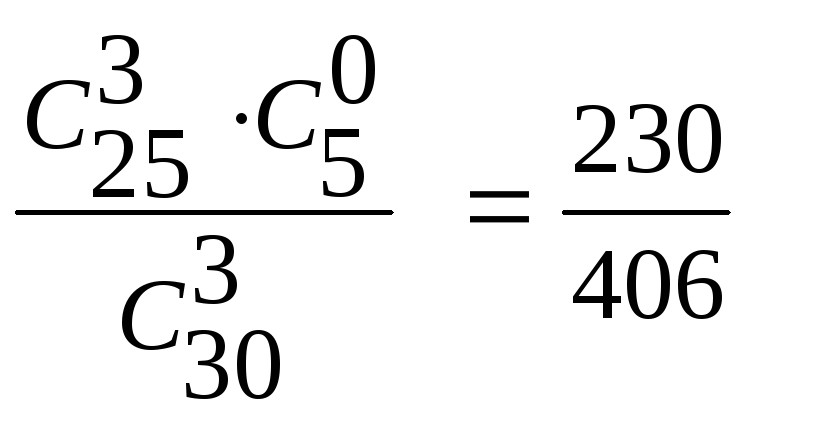Проверка: Р=Р₃(Х=0)+Р₃(Х=1)+Р₃(Х=2)+Р₃(Х=3) =

Закон распределения случайной величины Х:

X	0	1	2	3
P

◄

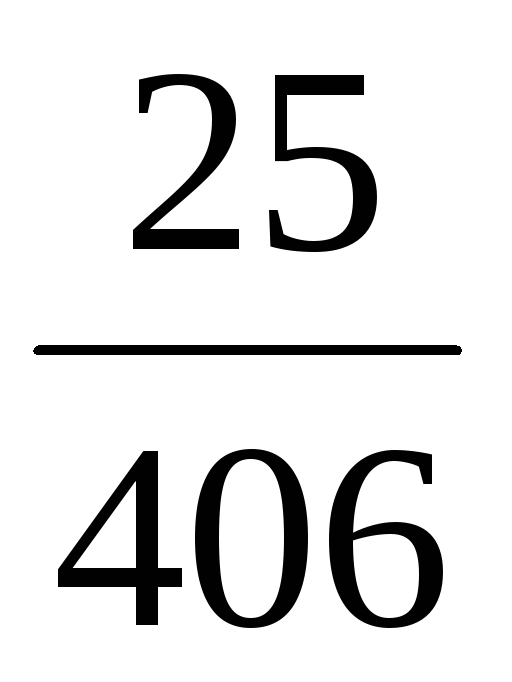
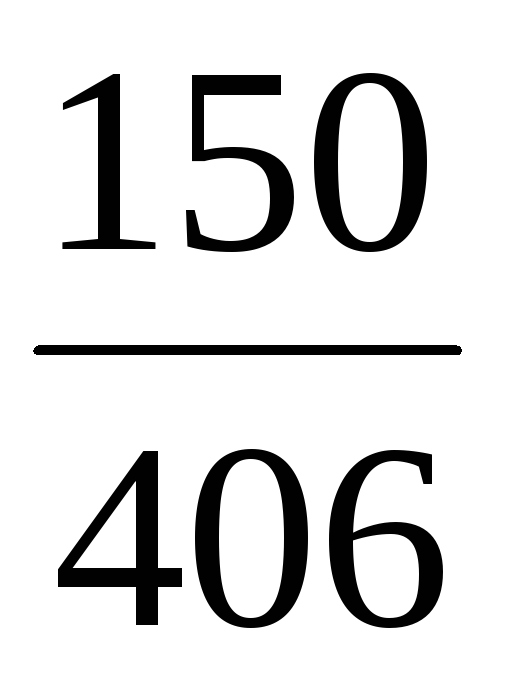
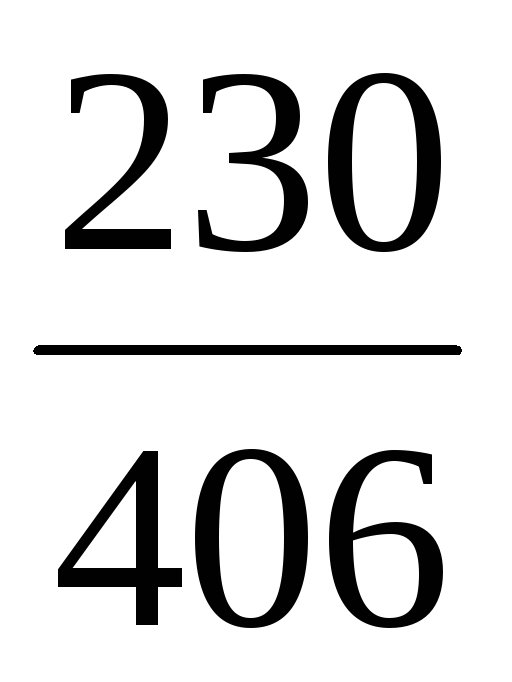
Замечание. Если - случайная величина, то для любой функции величина тоже является случайной величиной. Эта величина принимает значения с вероятностями , если функция взаимно однозначна . Если же значения совпадают для различных с величиной , то принимает общее значение с вероятностью, равной сумме вероятностей , отвечающих всем таким , для которых .

Пример. Дискретная случайная величина имеет закон распределения

X	-2	-1	0	1	2
Р	0.1	0.2	0.3	0.3	0.1

Построить закон распределения случайной величины Y = X² + 1.

Величина Y принимает значение 1 только, когда = 0, поэтому p₁ = P(Y=1) = 0.3. Значение 2 величина Y принимает , когда X = -1 и X = 1, поэтому p₂ = P(Y=2) = 0.2 + 0.3 = 0.5. Значение 5 величина Y принимает , когда X = -2 и X = 2, поэтому p₃ = P(Y=5) = 0.1 + 0.1 = 0.5. Следовательно, закон распределения случайной величины Y = X² + 1 имеет вид

Y	1	2	5
P	0.3	0.5	0.2

◄

■▬▬▬►

2. Совместные функции распределения нескольких величин. Рассмотрим сначала две дискретные случайные величины и . Пусть случайная величина принимает значения , а случайная величина принимает значения . Одновременное наступление событий и будем обозначать . Обозначим

.

Соответствие, которое каждой паре значений случайных величин и сопоставляет ее вероятность , называется совместным законом распределения случайных величин и .