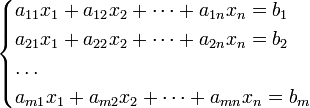- •Геометрические векторы. Основные понятия: определение, модуль,коллинеар- ность, равенство векторов, проекция вектора на направление другого вектора.
- •Линейные операции над геометрическими векторами. Правила треугольника и параллелограмма сложения векторов. Свойства линейных операций.
- •Линейная зависимость системы векторов. Необходимое и достаточное условие линейной зависимости системы векторов (доказательство).
- •Необходимое и достаточное условие линейной зависимости двух; трех векторов.
- •Определение линейного пространства. Размерность линейного пространства.
- •Базис плоскости; базис трехмерного пространства. Линейные операции над векторами в координатной форме.
- •Декартов ортонормированный базис плоскости; трехмерного пространства. Вычисление модуля вектора в ортонормированном базисе.
- •Теорема о вычислении скалярного произведения векторов в ортонормированном базисе
Теорема о вычислении скалярного произведения векторов в ортонормированном базисе
В
евклидовом (унитарном) пространстве
скалярное произведение векторов
 и
и
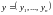 ,
заданных своими координатами в базисе
,
заданных своими координатами в базисе
 ,
вычисляется по правилу
,
вычисляется по правилу
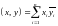 тогда и только тогда, когда базис
- ортонормированный.
тогда и только тогда, когда базис
- ортонормированный.
Нахождение модуля вектора, угла между векторами с помощью скаляр. произв.
Векторное произведение двух векторов; его свойства. Вычисление векторного произведения векторов в ортонормированном базисе.
Определение.
Векторным произведением 2-х векторов
называется вектор
 (Х-векторное
произведение)
1.
(Х-векторное
произведение)
1.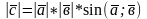 такой
что
такой
что
Длина вектора c равна S параллелограмма, построена на векторах и .

2. :
3. Направление вектора определяется по правилу буравчика или по правилу правой руки
Если вектор поворачивать к вектору по кратчайшему повороту, то направление правого винта показывает направление вектора .
Свойства векторного произведения.
1)
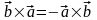 ;
;
2)
 ,
если
ïï
,
если
ïï или
=
0 или
=
0;
или
=
0 или
=
0;
3) (m )´ = ´(m ) = m( ´ );
4)
´(
+
 )
=
´
+
´
;
)
=
´
+
´
;
Векторное произведение в координатной форме.
5)
Если заданы векторы
(xa,
ya,
za)
и
(xb,
yb,
zb)
в декартовой прямоугольной системе
координат с единичными векторами
 ,
то
,
то
= =
I*
=
I* -J*
-J*
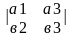 +K*
+K* =*
=* =ad-bc
=ad-bc
Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .
Вычисление векторного произведения векторов в ортонормированном базисе.
Смешанное произведение трех векторов; его свойства. Геометрический смысл смешанного произведения.
Определение.
Смешанным
произведением
векторов
,
и
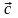 называется число,
равное скалярному произведению вектора
на вектор, равный векторному произведению
векторов
и
.(aXb)c
Обозначается
называется число,
равное скалярному произведению вектора
на вектор, равный векторному произведению
векторов
и
.(aXb)c
Обозначается
 или
(
,
,
).
или
(
,
,
).
Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах , и .v=|abc|
Геометрический смысл заключается в том, что по абсолютной величине смешанное произведение 2-х векторов = объему параллелепипеда, построенных на векторах
Объем этого параллелепипеда = произведению векторов V=| |
Свойства.
1)Смешанное произведение равно нулю, если:
а) хоть один из векторов равен нулю;
б) два из векторов коллинеарны;
в) векторы компланарны.abc=0 ck abc компланарны
2)
3)
4)
5) Объем треугольной пирамиды, образованной векторами , и , равен

6)Если
 ,
,
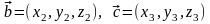 ,
то
,
то

Прямая на плоскости и в пространстве. Канонические и параметрические уравнения прямой. Уравнение прямой, проходящей через две данные точки.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 0. Это уравнение первого порядка называют общим уравнением прямой.
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
Это векторное уравнение может быть представлено в координатной форме:

Замечание. Каждые точки на прямой соответствует свое значение параметра t.
При движении точки по прямой параметра t непрерывно меняется.
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:
![]() .
.
Замечание. Каждые точки на прямой соответствует свое значение параметра t.
При движении точки по прямой параметра t непрерывно меняется.
Уравнение прямой
проходящей через 2 данные точки.


Уравнение плоскости в пространстве (вывод). Уравнение плоскости, проходящей через три данные точки.
Угол между плоскостями. Угол между прямой и плоскостью.

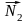
1
0

Угол между двумя плоскостями в пространстве связан с углом между нормалями к этим плоскостям 1 соотношением: = 1 или = 1800 - 1, т.е.
cos = cos1.
Определим угол 1. Известно, что плоскости могут быть заданы соотношениями:
 ,
где
,
где
(A1, B1, C1), (A2, B2, C2). Угол между векторами нормали найдем из их скалярного произведения:
 .
.
Таким образом, угол между плоскостями находится по формуле:


Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
Угол между прямой и плоскостью.
Определение. Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.

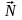

Пусть плоскость
задана уравнением
 ,
а прямая -
,
а прямая -
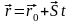 .
Из геометрических соображений (см. рис.)
видно, что искомый угол
= 900 - , где
- угол между векторами
и
.
Этот угол может быть найден по формуле:
.
Из геометрических соображений (см. рис.)
видно, что искомый угол
= 900 - , где
- угол между векторами
и
.
Этот угол может быть найден по формуле:

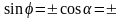
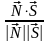

В координатной
форме:
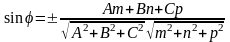
Матрицы. Основные понятия. Виды матриц: прямоугольная, квадратная, единичная, матрица-строка, матрица-столбец. Равенство матриц. Линейные операции над матрицами и их свойства.
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Определение. Прямоугольная таблица m·n чисел, расположенных в m строках и n столбцах называется прямоугольной (m,n) матрицей или просто матрицей.
Числа m и n называются порядками или размерностями матрицы.
Если m=n, то матрица называется квадратной матрицей порядка m.
Примеры:
![]() —
квадратная
матрица порядка 2,
—
квадратная
матрица порядка 2, 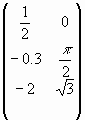 —
прямоугольная матрица,
—
прямоугольная матрица,
![]() —матрица-столбец,
—матрица-столбец, ![]() —
матрица-строка.
—
матрица-строка.
Две
матрицы называются равными, если они
имеют одинаковую размерность и равные
соответсвенные элементы: ![]()
Линейными операциями называются операции сложения и умножения на число.
Определение. Суммой
двух матриц одинаковой размерности
называется матрица той же размерности,
каждый элемент которой равен сумме
соответствующих элементов слагаемых: ![]() .
.
Определение. Произведением
матрицы на число называется матрица
той же размерности, каждый элемент
которой равен произведению соответствующего
элемента на число: ![]() .
.
Для операций сложения и умножения матрицы на число справедливо:
1·A=A,
0·A= ,
( A) = ( )A,
A+(B+C) = (A+B)+C,
A+B = B+A,
( + )A= A+ A,
(A+B) = A+ B.
где A, B, C — произвольные матрицы одинаковой размерности, — нулевая матрица той же размерности (читается “тэта”), и — произвольные числа.
Операция умножения матриц; ее свойства. Умножение матрицы-строки на матрицу-столбец. Примеры. Транспонирование матриц. Свойства операции транспонирования.
Операция умножения матрицы на матрицу определяется более сложным образом.
Определение. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если
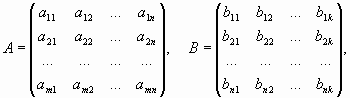
то произведением матриц A и B называется матрица
 ,
,
элементы которой вычисляются по формуле
![]() ,
, ![]() ;
;
произведение матриц A и B обозначается AB: C=AB.
Пример.
 .
.
Для произведения матриц соответствующих порядков справедливо:
A·B B·A,
(A + B) · C = A·C + B·C,
C·(A + B) = C·A + C·B,
(A·B) = ( A) ·B,
(A·B) ·C = A·(B·C).
Пусть ![]() .
Матрица
.
Матрица ![]() называется транспонированной
к матрице A,
если
называется транспонированной
к матрице A,
если![]()
Транспонированная
матрица также обозначается символами ![]() и
и ![]() .
.
Заметим,
что при транспонировании матрицы её
строки становятся столбцами матрицы ![]() ,
с теми же номерами, а столбцы - строками.
,
с теми же номерами, а столбцы - строками.
Теорема 2.4. Операция транспонирования матриц обладает следующими свойствами:
1) ![]() ;
;
2) ![]() ,
для любого действительного числа
,
для любого действительного числа ![]() ;
;
3) ![]() ;
;
4) ![]() ,
для любых матриц A и B, для которых имеют
смысл левые части равенств.
,
для любых матриц A и B, для которых имеют
смысл левые части равенств.
Определители квадратных матриц, миноры и алгебраические дополнения. Разложение определителя по строке или столбцу. Свойства определителей.
Определителем
квадратной матрицы А= называется число, которое может быть
вычислено по элементам матрицы по
формуле:
называется число, которое может быть
вычислено по элементам матрицы по
формуле:

det
A =
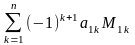 ,
где (1)
,
где (1)
М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k –го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Ф ормула
(1) позволяет вычислить определитель
матрицы по первой строке, также справедлива
формула вычисления определителя по
первому столбцу:
ормула
(1) позволяет вычислить определитель
матрицы по первой строке, также справедлива
формула вычисления определителя по
первому столбцу:
det
A =
 (2)
(2)
Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:

detA =
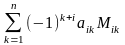 ,
i = 1,2,…,n.
(3)
,
i = 1,2,…,n.
(3)
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Миноры.
Выше было использовано понятие дополнительного минора матрицы. Дадим определение минора матрицы.
Определение. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.
Заметим, что вышесказанное применимо не только к квадратным матрицам, но и к прямоугольным.
Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.
Алгебраические дополнения.
Определение. Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы.
В частном случае, алгебраическим дополнением элемента матрицы называется его минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки
d = ai
1 Ai
1 +
ai 2 Ai
2 +...
+ ai n Ai
n
(i = ![]() )
)
или j- го столбца
d = a1 j A1 j + a2 j A2 j +... + an j An j (j = ).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Пример 2.4. Не
вычисляя определителя  ,
показать, что он равен нулю.
,
показать, что он равен нулю.
Решение. Вычтем
из второй строки первую, получим
определитель  ,
равный исходному. Если из третьей строки
также вычесть первую, то получится
определитель
,
равный исходному. Если из третьей строки
также вычесть первую, то получится
определитель  ,
в котором две строки пропорциональны.
Такой определитель равен нулю.
,
в котором две строки пропорциональны.
Такой определитель равен нулю.
Свойство1. Важным свойством определителей является следующее соотношение:
det A = det AT;
Свойство 2. det ( A B) = det A det B.
Свойство 3. det (AB) = detAdetB
Свойство 4. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.
Свойство 5. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.
Свойство 6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.
Определение: Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Свойство 7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
Свойство 8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.
Свойство 9. Если для элементов какой- либо строки или столбца матрицы верно соотношение: d = d1 d2 , e = e1 e2 , f = f1 f2 , то верно:

Обратная матрица. Определение, условие существования, алгоритм вычисления. Свойства обратных матриц.
Если существуют квадратные матрицы Х и А, удовлетворяющие условию:
XA = AX = E,
где Е - единичная матрица того же самого порядка, то матрица Х называется обратной к матрице А и обозначается А-1.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.
Рассмотрим общий подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, можно записать:
AX = E
 ,
i=(1,n), j=(1,n),
,
i=(1,n), j=(1,n),
eij = 0, i j,
eij = 1, i = j .
Таким образом, получаем систему уравнений:
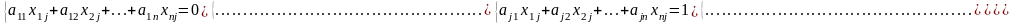 ,
,
Решив эту систему, находим элементы матрицы Х.
Пример. Дана
матрица А =
 ,
найти А-1.
,
найти А-1.



Таким образом, А-1= .
.
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:

 ,
,
где Мji- дополнительный минор элемента аji матрицы А.
Пример. Дана матрица А = , найти А-1.
det A = 4 - 6 = -2.
M11=4; M12= 3; M21= 2; M22=1
x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким образом, А-1= .
Cвойства обратных матриц.
Укажем следующие свойства обратных матриц:
(A-1)-1 = A;
2) (AB)-1 = B-1A-1
3) (AT)-1 = (A-1)T.
Ранг матрицы (определение). Вычисление ранга матрицы путем приведения ее к ступенчатому виду. Пример.
Порядок базисного минора матрицы называется рангом матрицы и обозначается Rg А.
Очень важным свойством элементарных преобразований матриц является то, что они не изменяют ранг матрицы.
Основа алгоритма - цикл по всем элементам главной диагонали. Для квадратной матрицы размера n будет n итераций. Для прямоугольной матрицы, состоящей из n строк и k столбов, число итераций будет равно min(n, k). Пусть i - счетчик итераций.
Каждый проход цикла устроен следующим образом.
Если A(i, i) равен нулю, то в прямоугольнике (i, i, n, k) ищем ненулевой элемент. Если он не найден, то выходим из цикла. Если он найден, и его координаты (i2, j2), то меняем местами i-ую строку с i2-ой, и j-ый столбец с j2-ым. Делим i-ую строку матрицы на A(i, i). Таким образом A(i, i) теперь равен 1.
При помощи вычитания i-го столбца из всех столбцов стоящих правее, и i-ой строки из всех строк стоящих ниже, с определенными коэффициентами, зануляем все элементы вида А(i+1, i), A(i+2, i), ... A(n, i) и A(i, i+1), A(i, i+2), ... A(i, k).
Переходим к следующей итерации.
После цикла остается подсчитать сколько единиц стоит на главной диагонали. Их кол-во равно рангу. Если же их нет, то ранг равен 1.
Пример:

Делим первую строку на 3.

Теперь вычитаем из второго и третьего столбца первый с коэффициентами 2/3 и 1/3 соответственно.

Вычитаем из второй и третьей строки первую с коэффициентами 2 и 1 соответственно.

и т.д. В итоге получим матрицу:

Следовательно ранг матрицы равен 3.
Системы n линейных уравнений с n неизвестными. Критерий единственности решения. Решение системы n х n методом Крамера.
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
|
(1) |
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно
Запись системы линейных уравнений в виде матричного уравнения. Решение системы n х n матричным способом.
Матричный метод решения систем линейных уравнений.
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.
Метод удобен для решения систем невысокого порядка.
Метод основан на применении свойств умножения матриц.
Пусть дана система уравнений:

Составим
матрицы: A =
 ;
B =
;
B =
 ;
X =
;
X =
 .
.
Систему уравнений можно записать:
AX = B.
Сделаем следующее преобразование: A-1AX = A-1B,
т.к. А-1А = Е, то ЕХ = А-1В
Х = А-1В
Для применения данного метода необходимо находить обратную матрицу, что может ыть связано с вычислительными трудностями при решении систем высокогопорядка.
Пример. Решить систему уравнений:

Х =
 ,
B =
,
B =
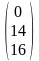 ,
A =
,
A =

Найдем обратную матрицу А-1.
=
det A =
 5(4-9)
+ 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
5(4-9)
+ 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
M11
=
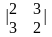 = -5; M21
=
= -5; M21
=
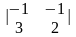 = 1; M31
=
= 1; M31
=
 = -1;
= -1;
M12
=
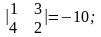 M22
=
M22
=
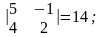 M32
=
M32
=

M13
=
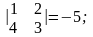 M23 =
M23 =
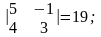 M33 =
M33 =

 A-1 =
A-1 =
 ;
;
Cделаем проверку:
AA-1
=
 =E.
=E.
Находим матрицу Х.
Х =
=
А-1В =
=
 .
.
Итого решения системы: x =1; y = 2; z = 3.
Несмотря на ограничения возможности применения данного метода и сложность вычислений при больших значениях коэффициентов, а также систем высокого порядка, метод может быть легко реализован на ЭВМ.
Решение системы m линейных уравнений с n неизвестными методом Гаусса. Пример. Определение числа решений по виду приведенной к ступенчатому виду расширенной матрицы системы.
Метод Гаусса.
(Карл Фридрих Гаусс (1777-1855) немецкий математик)
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:
Разделим обе части 1–го уравнения на a11 0, затем:
1) умножим на а21 и вычтем из второго уравнения
2) умножим на а31 и вычтем из третьего уравнения
и т.д.
Получим:
 ,
где d1j
= a1j/a11,
j = 2, 3, …, n+1.
,
где d1j
= a1j/a11,
j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Пример. Решить систему линейных уравнений методом Гаусса.
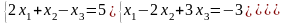
Составим расширенную матрицу системы.
А* =

Таким образом, исходная система может быть представлена в виде:
 ,
откуда получаем: x3
= 2; x2 = 5; x1
= 1.
,
откуда получаем: x3
= 2; x2 = 5; x1
= 1.