Метод зон френеля

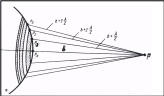Цель. Метод зон Френеля, используя принцип Гюйгенса-Френеля, применяется для нахождения амплитуды светового колебания, возбуждаемого в точке наблюдения Р сферической волны, распространяющейся в однородной среде из точечного источника S. Волновая поверхность такой волны симметрична относительно прямой SP.

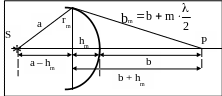
Суть метода. Френель разбил волновую поверхность на кольцевые зоны, построенные так, что расстояние от краев каждой зоны до точки Р отличается на . Из рис. видно, что расстояние b_m от внешнего края m-ой зоны до точки Р можно представить следующим образом

m = 0, 1, 2,….

где b – расстояние от вершины волновой поверхности О до точки Р.

Замечание. Колебания, приходящие в точку Р от аналогичных точек двух соседних зон, будут находится в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в отдельности, будут для соседних зон отличаться по фазе на .

Для оценки амплитуд колебаний нужно найти площади зон. Внешняя граница m-ой зоны выделяет на волновой поверхности сферический сегмент высоты h_m. Обозначим площадь этого сегмента S_m.. Тогда площадь m-ой зоны можно представить так

S_m = S_m – S_m-1

где S_m-1 – площадь сферического сегмента, выделяемого внешней границей (m – 1) – ой зоны.

Из рис. следует, что

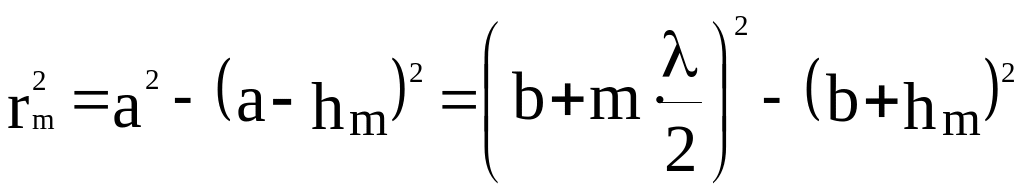
где а – радиус волновой поверхности, r_m – радиус внешней границы m – ой зоны. Возведя скобки в квадрат, получим

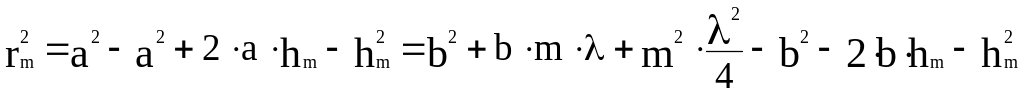откуда

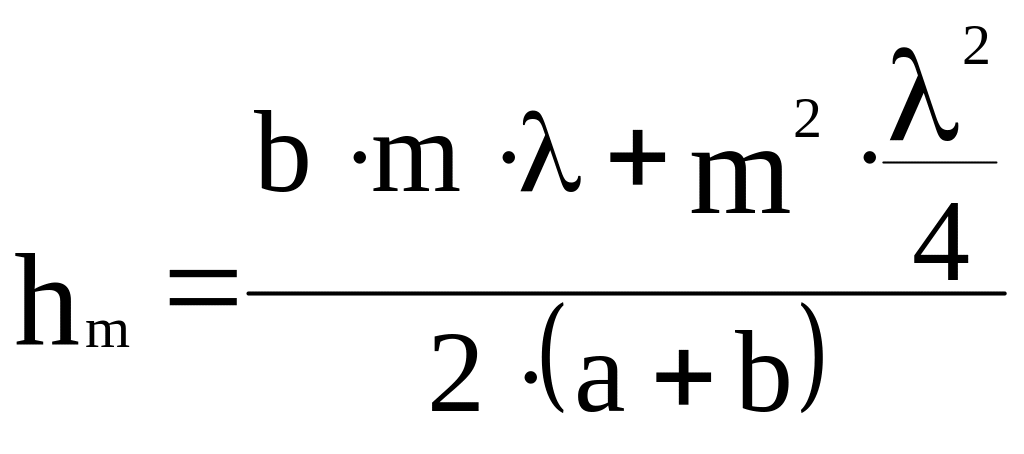
так как 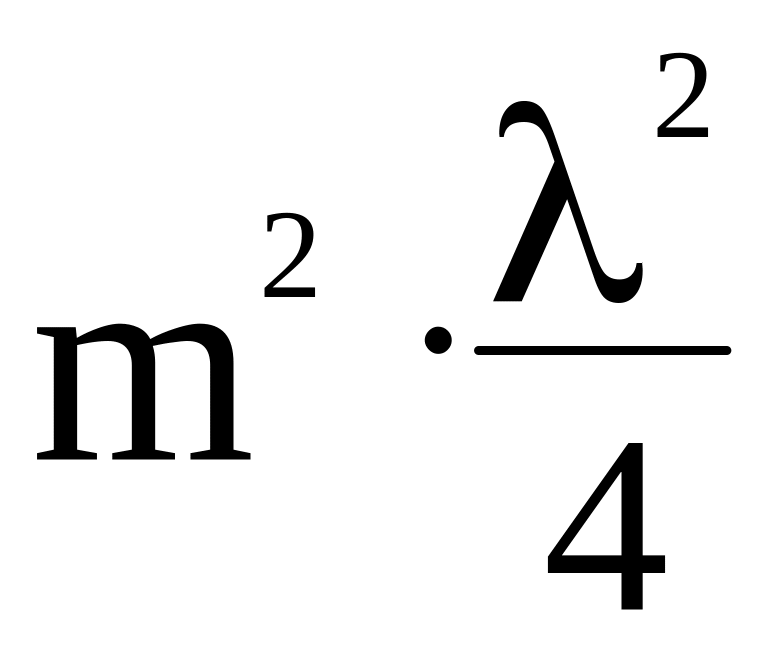мало, то это слагаемое можно приравнять нулю, то есть 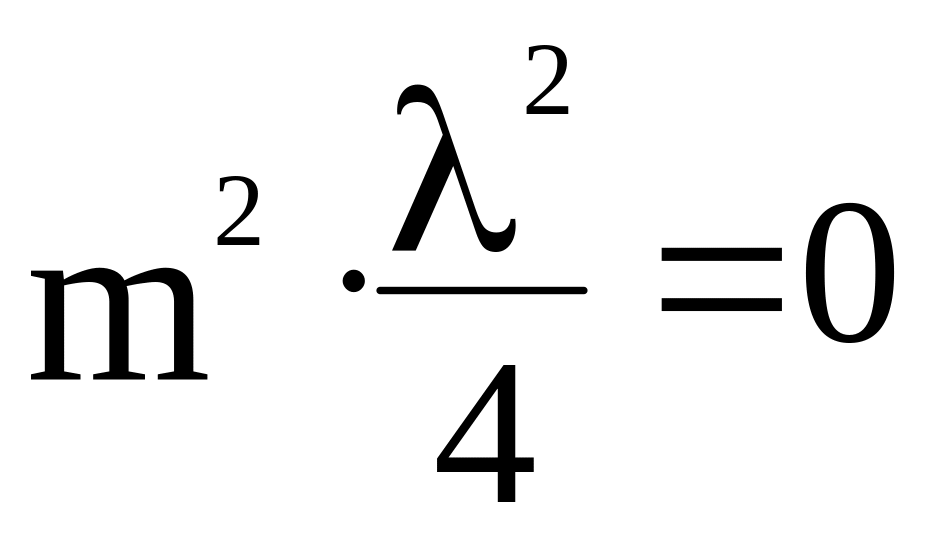. Тогда получим (1)

Площадь сферического сегмента равна S = 2Rh,

где R – радиус сферы, h – высота сегмента. Следовательно,

.

А площадь m – ой зоны Френеля

(2)

Полученное выражение не зависит от m. Это означает, что при не слишком больших m площади зон Френеля примерно одинаковы.

Оценим радиусы зон Френеля. Согласно вышесказанному

Так как при не слишком больших m высота сегмента h_m << a, то можно считать, . Подставив сюда выражение (1), найдем радиус внешней границы m – ой зоны Френеля:

(3)

Пример. Если положить a = b = 1 м и  = 0,5 мкм, то для радиуса первой (центральной) зоны получается значение r = 0,5 мкм.

Вывод. Итак, мы нашли, что площади зон Френеля примерно одинаковы. Расстояние b_m от зоны до точки Р медленной растет с увеличением номера зоны по линейному закону. Угол  между нормалью к элементам зоны и направлением на точку Р, также растет с возрастанием номера зоны. Все это приводит к тому, что амплитуда A_m колебания, возбуждаемого m – ой зоной в точке Р, монотонно убывает с ростом m. Таким образом, амплитуда колебаний, возбуждаемых в точке Р зонами Френеля, образуют монотонно убывающую последовательность.

A₁ > A₂ > A₃ > … > A_m-1 > A_m > A_m+1 > …

Фазы колебаний, возбуждаемых соседними зонами, отличаются на . Поэтому амплитуда результирующего светового колебания в точке Р может быть найдена алгебраически:

А = А₁ – А₂ + А₃ – А₄ + … (4)

В этом выражении все амплитуды от нечетных зон входят с одним знаком, а от четных зон – с другим. Выражение (4)_ запишем в виде

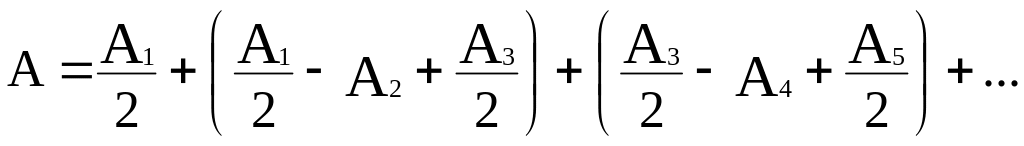(5)

Вследствие монотонного убывания A_m можно приближенно считать, что

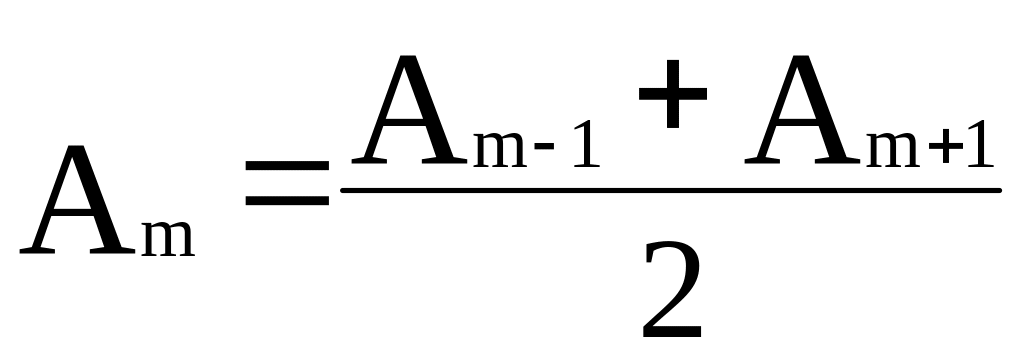
При этом условии выражения, заключенные в круглые скобки, будут равны нулю и формула (5) упрощается

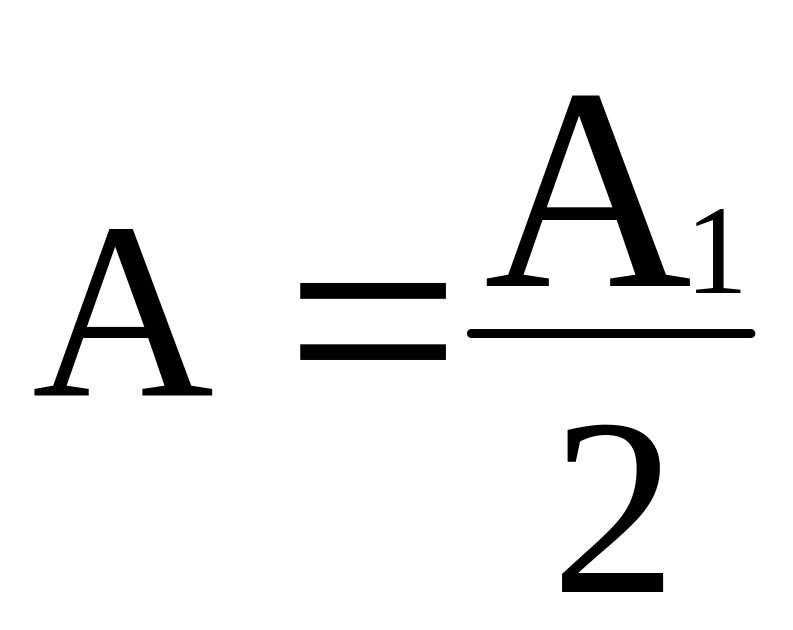
Вывод. Полученный нами результат означает, что амплитуда, создаваемая в некоторой точки Р сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной. То есть, действие всей волновой поверхности эквивалентно половине действия центральной зоны.