7. Предел комплексных функций

Определение 2.3.

Комплексное число называется пределом комплексной функции в точке , если для , , что для , .

О бозначение: .

Рассмотрим две комплексные плоскости и .

Тот факт, что геометрически выглядит следующим образом: точки находятся в –окрестности точки (круге радиуса с центром в точке ), если точки находятся в –окрестности точки (круге радиуса с центром в точке ) (рис.2.5).

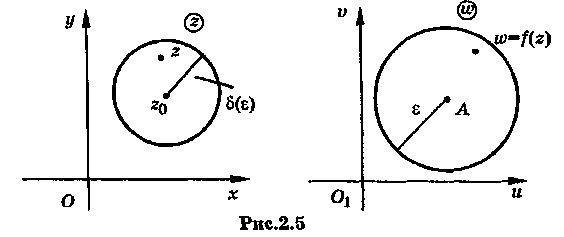
Эквивалентным предыдущему является следующее.

Определение 2.4.

Комплексное число А называется пределом функции в точке если для любой последовательности , последовательность значений функции стремится к . (Равносильность двух определений докажите самостоятельно).

Теорема 2.4.

Если комплексная функция имеет предел в точке равный , то действительная и мнимая части комплексной функции имеют пределы в этой точке

,

и наоборот.

Доказательство.

1. Пусть

для .

Но , .

По теореме 2.1., если , то

, а , т.е.

и ,

т.е. для любой последовательности последовательности значений функций и : и стремятся соответственно к и , т.е. функции и имеют пределы в точке , равные и соответственно.

2. Пусть , и

тогда используя вторую часть теоремы 2.1 получаем, что

.

Теорема доказана.

Из теоремы 2.4. следует, что известные из курса матема­тического анализа, теоремы о пределах для функций нескольких действительных переменных остаются справедливыми и для функций комплексного переменного.

Так, если функции и имеют конечные пределы при , то имеют место следующие соотношения:

,

,

.

8.Непрерывность комплексных функций

Определение 2.5.

Комплексная функция называется непрерывной в точке если для , , что для всех , таких что выполняется неравенство .

Из данного определения непрерывности функции и определения предела функции естественно вытекает следующее:

Определение 2.6.

Комплексная функция называется непрерывной в точке если .

Равносильность двух последних определений очевидна в случае, если является предельной точкой области определения функции.

Введем обозначения

, , , ;

;

.

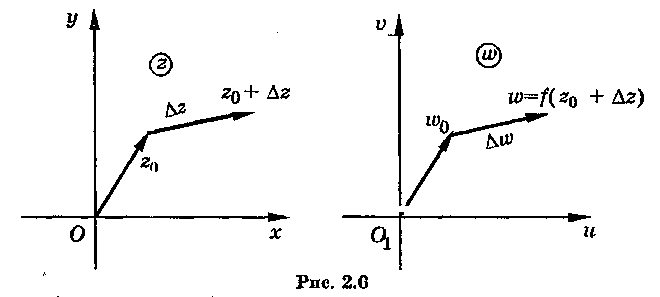
Дадим геометрическое истолкование приращениям независимой переменной и функции (рис. 2.6).

П риращению на плоскости соответствует вектор с началом в точке и с концом в точке ; приращению функции на плоскости соответствует вектор ; с началом в точке и с концом в точке

Из равенства имеем

; ,

значит .

Введя обозначения

, ,

имеем .

Определение 2.7.

Функция называется непрерывной в точке , если .

Равносильность этого определения непрерывности функций с двумя предыдущими непосредственно вытекает из предыдущих рассуждений.

Теорема 2.5.

Если комплексная функция непрерывна в точке , то непрерывны в этой точке действительная и мнимая её части:

,

и наоборот.

Доказательство.

1. Пусть комплексная функция непрерывна в точке . На основании последнего определения имеем:

.

Заметим, что .

Условие равносильно условиям

,

Последнее означает, что функции , непрерывны в точке (См. непрерывность функций 2-х действительных переменных).

2. Пусть функции и непрерывны в точке , тогда

,

при ,

т.е. комплексная функция непрерывна в точке .

Теорема доказана.

Т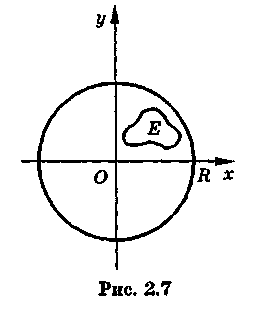 еорема даёт возможность перенести на комплексные непрерывные функции свойства непрерывных действительных функций двух действительных переменных. Чтобы сформулировать эти свойства вспомним некоторые определения из теории метрических пространств, взяв в качестве метрического пространства пространство комплексных чисел.

Определение 2.8.

Точка называется предельной точкой множества комплексных чисел , если в любой –окрестности точки : находятся точки , .

Определение 2.9.

Множество комплексных чисел называется ограниченным, если существует круг , включающий в себя множество (рис. 2.7).

О пределение 2.10.

Множество комплексных чисел называется замкнутым, если оно содержит все свои предельные точки.

Пример 1.

Любой замкнутый круг является множеством замкнутым (рис. 2.8).

Теорема 2.6.

Всякая комплексная непрерывная функция ограничена на замкнутом ограниченном множестве комплексных чисел , т.е. постоянная , что для имеем: .

Доказательство.

Предположим противное. Пусть функция не является ограниченной на замкнутом множестве .

Тогда для любого натурального числа найдется такая точка , что

.

Так как по условию теоремы множество ограничено, то — ограниченная последовательность.

В силу теоремы Больцано-Вейерштрасса, из ограниченной последовательности можно выделить сходящуюся подпоследовательность .

Пусть . Так как множество является замкнутым, то точка принадлежит множеству . Функция непрерывна на множестве , поэтому вследствие непрерывности в точке будем иметь

что невозможно, так как из следует, что

.