15. Степенная функция с натуральным показателем

Степенная функция с натуральным показателем – это функция вида , где – натуральное, a – комплексная переменная.

Свойства:

1. Степенная функция определена на всей комплексной плоскости, так как для любого комплексного числа существует .

2. Множество значений степенной функции есть также все множество комплексных чисел.

Докажем это утверждение, т.е. покажем, что функция принимает любое комплексное значение, другими словами покажем, что при любом комплексном числе уравнение разрешимо относительно .

Пусть , ,

где , , , – одно из значений, например, главное значение . Тогда уравнение примет вид или .

Модуль левой части равен , аргумент – . Модуль правой части равен , аргумент – .

Два комплексных выражения равны между собой тогда и только тогда, когда модули этих выражений равны, а аргументы отличаются на число кратное , т.е.

Последняя система, очевидно, равносильна исходному уравнению. Имеем ,

Таким образом нами показано, что при любом уравнение имеет решений, определяемых формулой , где .

(В формуле вместо можно брать и другие значения, отличные от значений , но новых решений, как легко проверить, получать не будем). Очевидно, при уравнение имеет решение .

3. Степенная функция аналитична во всей комплексной плоскости. Это утверждение следует из дифференцируемости функции

как произведения дифференцируемых функций , у каждой из которых существует производная .

Аналитичность можно доказать и по другому. Покажем это в случае .

;

, ;

; ;

; .

Условия Коши–Римана выполняются во всех точках плоскости.

; .

Частные производные , , , непрерывны на всей комплексной плоскости, а тогда по известной теореме–условии аналитичности функций в области функция будет аналитической во всей комплексной плоскости.

4. Степенная функция однолистна во всяком углу величины с вершиной в начале координат. (Под углом здесь и далее понимаем открытый угол, не включающий в себя сторон).

Докажем утверждение следующим образом: посмотрим, где возможно нарушение однолистности функции в комплексной плоскости, т.е. где при будем иметь .

Пусть , , где , ,

Тогда , , ,

так как два комплексных выражения равны между собой тогд только тогда, когда равны их модули, а аргументы отличав на число, кратное .

Из последних равенств получим , , .

Мы видим, что нарушение однолистности возможно в точках и , у которых одинаковые модули, а аргументы отличаются на числа:

, ,

Э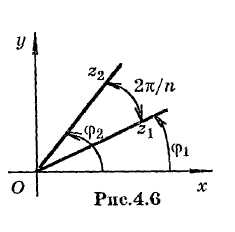 то означает, что внутри угла (рис.4.0) нарушение однолистности произойти не может, а, значит, внутри этого угла функция однолистна.

5. Степенная функция всякий открытый угол с вершиной в начале координат на плоскости конформно отображает на открытый угол с вершиной в начале координат на плоскости .

Как мы показали, функция однолистна в указанном углу. Кроме этого, в каждой точке угла существует производная , а такие отображения, как мы знаем, конформны.

Покажем теперь, что образом угла при отображении является угол .

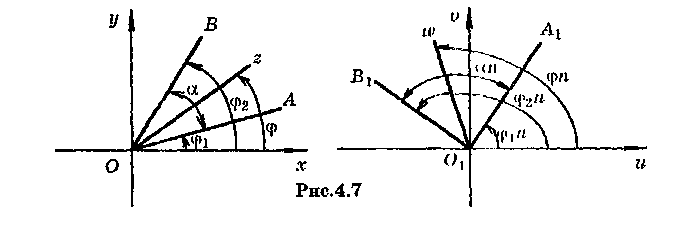
Рассмотрим произвольный луч образующий угол с осью при условии (рис.4.7), Легко проверить, используя формулу , что образом луча при отображении будет луч , обрааующий угол с осью , так как , если .

Если луч будет вращаться от положения луча к положению луча , то он опишет угол . Тогда образ луча – луч опишет угол , перемещаясь от луча к лучу .