24. Группа классов вычетов взаимно простых с модулем.

Определение. Приведенной системой вычетов по модулю m называется совокупность всех вычетов из полной системы, взаимно простых с модулем m .

Приведенную систему обычно выбирают из наименьших неотрицательных вычетов. Ясно, что приведенная система вычетов по модулю m содержит j ( m ) штук вычетов, где j ( m ) – функция Эйлера – число чисел, меньших m и взаимно простых с m . Пример. Пусть m = 42. Тогда приведенная система вычетов суть:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Лемма 2. 1) Любые j ( m ) чисел, попарно не сравнимые по модулю m и взаимно простые с модулем, образуют приведенную систему вычетов по модулю m .

2) Если ( a,m ) = 1 и x пробегает приведенную систему вычетов по модулю m, то аx так же пробегает приведенную систему вычетов по модулю m.

Доказательство. Утверждение 1) – очевидно. Докажем утверждение 2). Числа аx попарно несравнимы (это доказывается так же, как в лемме 1 этого пункта), их ровно j ( m ) штук. Ясно также, что все они взаимно просты с модулем, ибо (a,m)=1, (x,m)=1 (ax,m)=1 . Значит, числа аx образуют приведенную систему вычетов.

Таковы определения и основные свойства полной и приведенной систем вычетов, однако в багаже математических знаний существует еще целый ряд очень интересных и полезных фактов, касающихся систем вычетов. Если умолчать про них в этом пункте, то это, боюсь, будет прямым нарушением Закона Российской Федерации об Информации, злонамеренное утаивание которой является, согласно этому закону, административно и, даже, уголовно наказуемым деянием. Кроме того, без знакомства с дальнейшими важными свойствами систем вычетов пункт 17 получится весьма куцым. Продолжим.

Если в Zn выбрать все классы, взаимно простые с модулем n, то они образуют мультипликативную группу классов вычетов, взаимно простых с модулем n. (группу по умножению). Она обычно обозначается Gn.

25. Теоремы Эйлера и Ферма.

Теорема Эйлера: Если НОД(а,m)=1,то _.

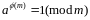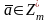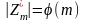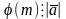Док-во: Если НОД(а,m)=1,то ,то ,то 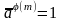,то ,то

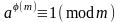
Замечание. Теорема Эйлера дает еще один способ вычисления 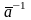: Если НОД(а,m)=1,то

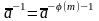
Теорема (малая теорема Ферма). Пусть р - простое число, которое не делится не р, тогда 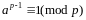. Док-во: 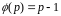по теореме Эйлера: _.

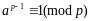Следствие. Если р – простое число, то

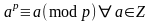
Док-во. 1 случай: а не кратно р, то НОД(а, р)=1

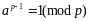
Домножим на а:

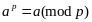
2 случай: 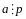, то 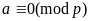- тождество очевидно

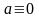
Замечание. Если m – простое число и НОД(а,р)=1, то

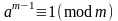
НОД(а, m)=1 и не следует, что m – простое.

26. Сравнения с одной неизвестной.

Опр. Сравнение вида ax≡b(mod m) наз. сравнением первой степени.

Свойства:

1. НОД(a,m) = 1 имеет единственное решение

2. НОД(a,m) = d >1

a = a₁d

b = b₁d

m = m₁d

b:d

Подставим a₁d×x≡ b₁d(mod m₁d) сократим на d

a₁×x≡ b₁(mod m₁)

НОД(a₁,m₁) = 1

x≡x₀(mod m₁)

т.е это сравнение по mod m₁ имеет одно решение. По модулю m оно буде иметь решение d.

x₀, x₀+m₁, x₀+2m₁, x₀+(d-1)m₁ – эти числа по модулю m₁ сравнимы, по модулю m, они не сравнимы, значит они имеют решение.