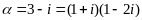- •Нод и нок нескольких целых чисел.
- •Конечные цепные дроби. Представление числа в виде конечной цепной дроби.
- •Подходящие дроби. Свойства подходящих дробей.
- •Систематические числа.
- •Простые числа. Свойства простых чисел.
- •Простые числа. Теорема Евклида о бесконечности множества простых чисел.
- •Простые числа. Решето Эратосфена.
- •Основная теорема арифметики.
- •Теорема о делимости натуральных чисел, разложенных на простые множители.
- •Кольцо целых гауссовых чисел . Норма целого гауссового числа и ее свойства. Пифагоровы числа.
- •Теорема о делении с остатком в кольце целых гауссовых чисел. Делители единицы (единицы) в кольце .
- •Делимость целых гауссовых чисел.
- •Линейные диофантовы уравнения. Представление всех решений линейного диофантова уравнения.
- •Количество и сумма натуральных делителей. Мультипликативные числовые функции.
- •Целая часть числа и ее свойства.
- •Сравнения и их свойства.
- •Полная система вычетов. Признак полной системы вычетов.
- •Приведенная система вычетов. Функция Эйлера. Признак приведенной системы вычетов.
- •Основная лемма о приведенных системах вычетов по двум взаимно простым модулям. Мультипликативность функции Эйлера.
- •Формула для вычисления функции Эйлера. Лемма Гаусса о сумме значений функции Эйлера по всем делителям данного числа.
- •Признак делимости Паскаля. Признак делимости на 2, 3, 4 и 5.
- •Признак делимости Паскаля. Признак делимости на 6, 7 и 8.
- •Признак делимости Паскаля. Признак делимости на 9 и 11.
- •Группа классов вычетов взаимно простых с модулем.
- •Теоремы Эйлера и Ферма.
- •Сравнения с одной неизвестной.
- •Линейные сравнения: критерий разрешимости и количество решений.
- •Периодические дроби. Теоремы о преобразовании несократимой дроби в периодическую дробь.
- •Правила преобразования периодической дроби в обыкновенную дробь.
- •Системы линейных сравнений. Система двух линейных сравнений и теорема о ее разрешимости. Китайская теорема об остатках.
- •Первообразные корни. Существование первообразных корней по простому модулю.
- •Индексы по простому модулю.
- •Теорема о свойствах индексов и следствие из нее.
- •Формула перехода от системы индексов с основанием к системе индексов с основанием (пример 1).
- •Двучленные сравнения. Решение двучленных сравнений. Квадратичные вычеты. Критерий Эйлера.
- •Теорема
- •Теорема
- •Критерий Эйлера
Теорема о делимости натуральных чисел, разложенных на простые множители.
Теорема:
Пусть n=p1α1∙
p2α2∙
….∙ psαs
– каноническое разложение числа n,
n δ
δ=
p1β1∙
p2β2∙
….∙ psβs
, где 0≤βi≤α
(*).
δ
δ=
p1β1∙
p2β2∙
….∙ psβs
, где 0≤βi≤α
(*).
 Доказательство:
n
δ
=> n=δ∙q
=> простые делители δ
входят в каноническое разложение числа
n с
показателем, не меньшим тех, с которыми
они входят в каноническое разложение
числа δ.
Поэтому δ
имеет вид (*)
Доказательство:
n
δ
=> n=δ∙q
=> простые делители δ
входят в каноническое разложение числа
n с
показателем, не меньшим тех, с которыми
они входят в каноническое разложение
числа δ.
Поэтому δ
имеет вид (*)
δ= p1β1∙ p2β2∙ ….∙ psβs
0≤βi≤αi (*)
В обратную сторону, каждое δ вида (*) делит n.
Кольцо целых гауссовых чисел . Норма целого гауссового числа и ее свойства. Пифагоровы числа.
О пределение:
Целым гауссовым числом наз. комплексное
число a+bi,
где а,в – целые числа.
пределение:
Целым гауссовым числом наз. комплексное
число a+bi,
где а,в – целые числа.
Теорема: <Z[i],+,∙> - коммутативное кольцо с 1. Док-во: 1) сложение и умножение – бинарные алгебраические операции. 2) <Z[i],+> - абелева группа: 1. ассоциативность (следует из ассоциативности сложения в цепи). А=bq+r 0≤r<|b| α=a+bi N(α)=a2+b2
Определение: Нормой числа α=a+bi из Z[i] наз. N(α)=a2+b2.
Св-ва
нормы:
N(α)≥0
N(α)=
α .
Док-во:
α=a+bi α
=
(a+bi) (a–bi)= a2+b2
N(α)=
N(
.
Док-во:
α=a+bi α
=
(a+bi) (a–bi)= a2+b2
N(α)=
N( )
)
Св-во мультипликативности нормы: N(α∙β)= N(α)∙ N(β). Док-во: α=a+bi β =с+di
α∙β=(ac–bd)+(ad+bc)i N(α∙β) =(ac–bd)2+(ad+bc)2=a2c2–2abcd+b2d2+
+a2d2+2abcd+b2c2= a2c2+a2d2+b2d2+b2c2= a2(c2+d2)+b2(d2+c2)=
=(d2+c2)(a2+b2)= (a2+b2)(c2+d2)=N(α)∙ N(β)
Замечание1: Если каждое из двух чисел - сумма двух квадратов, то их произведение также может быть записано, как сумма двух квадратов.
5= 12+22 13= 22+32 5∙13=65=42+72 либо 65=12+82
Замечание2: N(α2)= N(α)2 a2+b2=c2
Пифагоровыми числами называются такие натуральные числа а, b, с, что a2+b2=c2.
Теорема о делении с остатком в кольце целых гауссовых чисел. Делители единицы (единицы) в кольце .
Т:
Пусть α,
β
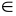 Z[i],
β
Z[i],
β
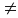 0,
тогда
0,
тогда
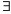 целые гауссовы числа
целые гауссовы числа
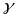 ,
,
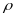
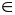 Z[i],
что
Z[i],
что

Док-во:
Рассмотрим
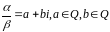 .
Выберем m,
n
.
Выберем m,
n Z:
|a–m|
Z:
|a–m|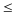
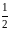 ,
|a–n|
,
|a–n|
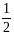 ,
,
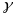 :=m+ni,
:=m+ni,
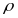 :=
:= ,
,
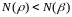 ,
,
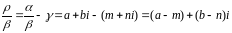 ,
,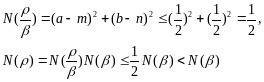
Делители единицы
Опр.
Делитель единицы
 :
:

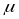 такое, что
такое, что
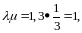 3 не является делителем единицы в Z.
3 не является делителем единицы в Z.
Теорема. Делителями единицы в кольце z[i] явл те, норма кот = 1.
Док-во:
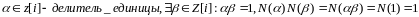
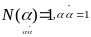
Следствие. В кольце Z[i] только 4 делителя единицы: +–1, +–i
Док-во:
N(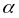 )=1,
a2+b2=1,
a=1, b=0, a=–1,b=0, a=0, b=1, a=0, b=–i
)=1,
a2+b2=1,
a=1, b=0, a=–1,b=0, a=0, b=1, a=0, b=–i
Делимость целых гауссовых чисел.
Целое
гауссово число π наз простым г.ч, если
в любом его представлении в виде
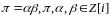 либо
либо
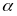 либо
либо
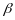 явл делителями1.
явл делителями1.
Целое
число
 наз
простым г.ч, если его не можно представить
в виде
наз
простым г.ч, если его не можно представить
в виде
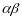 ,
где норма каждого больше 1. N(α)>1,
N(β)>1.
,
где норма каждого больше 1. N(α)>1,
N(β)>1.
Основная теорема:
Всякое
целое г.ч. α 0
разложимо в произведение простых чисел
0
разложимо в произведение простых чисел
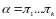 ,
все эти числа не обязательно различны
и такое разложение единственное.
,
все эти числа не обязательно различны
и такое разложение единственное.
Если
не однозначно t=k
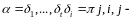 делители
единицы,
делители
единицы,
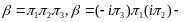 одинаковые
разложения
одинаковые
разложения
Док-во
проводим индукцией по норме n.
База: n=1,
то
 -делитель
1, разложение возможно с кол-вом множителей,
равным 0. Посылка: считаем, что для всех
гауссовых чисел с
-делитель
1, разложение возможно с кол-вом множителей,
равным 0. Посылка: считаем, что для всех
гауссовых чисел с
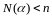 утверждение
верно. Берем
утверждение
верно. Берем
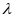 (возможны
2 случая)
(возможны
2 случая)
1:
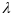 - простое г., число множителей равно 1.
- простое г., число множителей равно 1.
2:
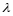 не
является простым гауссовым, тогда его
можно представить в виде произведения
не
является простым гауссовым, тогда его
можно представить в виде произведения
 ,
,
 .
Возвращаемся к предположению индукции
.
Возвращаемся к предположению индукции
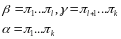 док
существование разложения.
док
существование разложения.
Однозначность:
предпол, есть еще одно разлож, если
левые части равны, то равны и правые
части
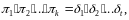
 .
Может так4 случиться, что каждое из
.
Может так4 случиться, что каждое из
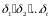 взаимно просто с
взаимно просто с
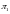
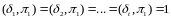 ,
но этого может и не быть, значит,
,
но этого может и не быть, значит,
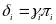
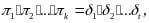 t–1=k–1
t=k
t–1=k–1
t=k
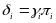
Пример:
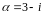 явл
ли простым гауссовым числом?
явл
ли простым гауссовым числом?
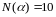 ,
10=2*5, N(1+i)=2,
N(1-2i)=5
,
10=2*5, N(1+i)=2,
N(1-2i)=5
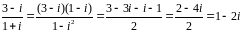 ,
,