40. Двучленные сравнения. Решение двучленных сравнений. Квадратичные вычеты. Критерий Эйлера.

Опр. Сравнение вида Axⁿ=B (mod m) (1) наз. двучленным сравнением, где n – натуральное. Axⁿ = a (mod m) (1^/)

В дальнейшем будем считать, что m – простое число, m=p>2.

Теорема. Пусть d=НОД(n,p–1). Тогда если d не делит ind a, то (1) не имеет решений. Если d делит ind a, то (1) имеет d решений. Док-во: Проиндексируем (1):

n ind x = ind a (mod(p–1)) это линейное сравнение относительно неизвестного ind x. По определению сравнение не имеет решений, если d не делит ind a. Значит, ind x имеет d решений, если d делит ind a.

Опр. В (1) а наз. вычетом n-ой степени по модулю p, p>2, р не делит а и наз. невычетом, если сравнение (1) не имеет решений.

Теорема. По простому модулю р (р – простое, р>2) у сравнения xⁿ = a (mod р) число вычетов равно 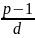, где d=НОД(n,p–1). Док-во: По определению по простому модулю р число классов, взаимно простых с модулем, будет р-1. Поскольку модуль простой, то всегда найдётся первообразный корень. Значит, есть возможные индексы: 1,2, … , р–1. Среди этих чисел на d делятся . По предыдущей теореме сравнение имеет решение, когда ind делится на d. Значит, вычетов будет .

Теорема. Если d=НОД(n,p–1) и р не делит а, то все решения сравнения xⁿ = a (mod р) совпадают с решениями сравнения x^d = a (mod р). Док-во: По теореме 1 из этого параграфа сравнение либо не имеет решений, либо их решения совпадут.

Теорема. Если d=НОД(n,p–1), (р–1) кратно n, а является вычетом по модулю р тогда и только тогда, когда x в степени =1 (mod р). Док-во:

ind a=0(mod р-1)<=> ind a=(p-1)t, t ϵ Z <=>

<=>ind a=dt <=> ind aкратно d.

C₀x²+c₁x+c₂=0(mod р), р – простое число. Будем считать, что C₀ не кратно р, иначе получим сравнение первой степени.

Как сделать, чтобы коэффициент при C₀ был сравним с р?

НОД(C₀,р)=1

C₀^р–1=1(mod р)

C₀^р–1x²+ C₀^р–2c₁x+ C₀^р–2c₂=0(mod р)

C₀^р–2c₁=b₁

C₀^р–-2c₂ =b₂

Получили х²+b₁x+b₂=0(mod р)

1 случай: b₁ – чётное число: (х+ b₁/2)²= b₁²/4– b₂(mod р), тогда b₁+p – чётное.

2 случай: b₁ – нечётное число: х²+(b₁+р)x+b₂=0(mod р)

Опр. Число а, для которого сравнение х² =а(mod р) имеет два решения, называется квадратичным вычетом.

Теорема

а- квадратичный вычет по модулю р а в степени =1(mod р)

Теорема

а- квадратичный вычет по модулю р  а в степени = –1(mod р).

Док-во. Необходимость. Из теоремы Ферма а в степени

=1(mod р) или а в степени - 1=0(mod р).

Откуда а ^(p-1) -1= (а ^ -1)( а ^ +1) =0(mod р).

а- квадратичный вычет

a^(p-1)/2 не =1(mod р)

а ^ не кратно р, т.е. а ^ = -1(mod р).

Достаточность.

а в степени = –1(mod р), тогда и а в степени = 1(mod р).

Критерий Эйлера

а является квадратичным вычетом или невычетом по модулю р в зависимости от того, какое из сравнений выполняется:

если а в степени = 1(mod р), то а – квадратичный вычет;

если а в степени = –1(mod р), то а – квадратичный невычет.