54. Интегрирование простейших иррациональных выражений.

Класс иррациональных функций очень широк, поэтому универсального способа их интегрирования просто быть не может. В этой статье попытаемся выделить наиболее характерные виды иррациональных подынтегральных функций и поставить им в соответствие метод интегрирования.

Используя метод непосредственного интегрирования, достаточно просто находятся неопределенные интегралы вида  , где p – рациональная дробь, k и b – действительные коэффициенты.

Бывают случаи, когда уместно использование метода подведения под знак дифференциала. Например, при нахождении неопределенных интегралов вида  , где p – рациональная дробь.

еопределенные интегралы иррациональных функций вида   находятся методом подстановки. В зависимости от рациональных чисел m, n и p вводят следующие новые переменные:

1. Если p - целое число, то принимают 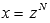 , где N - общий знаменатель чисел m и n.

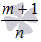2. Если   - целое число, то 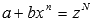 , где N - знаменатель числа p.

3. Если   - целое число, то вводят новую переменную 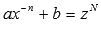 , где N - знаменатель числа p.

55. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка.

Функцию с переменными sin x и cos x, над которыми выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать R(sin x;cos x), где R - знак рациональной функции.

Вычисление неопределенных интегралов типа сводится к вычислению интегралов от paциoнaльнoй фyнкции подстановкой   , которая называется универсальной.

Действительно,

 ,

Поэтому

где R₁(t) - рациональная функция от t. Обычно этот способ весьма громоздкий, зато он всегда приводит к результату.

На практике применяют и другие, более простые подстановки, в зависимости от свойств (и вида) подынтегральной фyнкции. В частнocти, удобны следующие правила:

1)  если  функция  R(sinx;cos x)   нечетна  относительно  sinx,  т.е. R(— sinx;cos x)=— R(sin x;cos x), то подстановка cosx=t рационализирует интеграл;

2)  если  функция  R(sinx;cos x)   нечетна  относительно  cosx,  т.е. R(sinx; - cosx)=—R(sinx;cosx), то делается подстановка sinx=t;

3)  если функция  R(sin x; cos x)   четна  относительно sinx   и  cosx R(— sin x; - cos x)=R(sin x; cos x), то интеграл рационализируется подстановкой tgx=t. Такая же подстановка применяется, если интеграл имеет вид

56. Интегральные суммы. Понятие определенного интеграла.

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

(фото) криволинейн трапеция, разделена (.) x_1, x_2, x₃…x_n

A=x₀…x_n=b. x₀<x₁<…<x_n. x₁-x₀₌đ(дельта)x_1. x₂-x₁= đx_2..

ξ € [x_i-1, x_i]. F(ξ_i). S_n=f(ξ_i)дельта х₁+ f(ξ₂)дельта х₂+…+ f(ξ_n)дельта х_n=É_i=1…nf(ξ_i)дельта х_i (1).

Надо разбить на n-частей n→∞. Чем больше частей – тем точнее найдем площадь.

ОПр: Опред интегралом назв рпедел, к котор стремится интегр сумма при →0 наиб част интерв. Q=lim_{max дельта х1→0, n→∞}S_n=⌡^b_af(x)dx – интеграл Риммана.