Коэффициент корреляции Пирсона
Термин корреляция» был введен в науку выдающимся английским естествоиспытателем Френсисом Гальюном в 1886 г Однако точную формулу для подсчета коэффициента корреляции разработал его ученик Карл Пирсон Знакомство с корреляционным анализом мы начнем с изучения этого коэффициента Сам коэффициент характеризует наличие только линейной связи между признаками обозначаемыми как правило символами X и У Формула расчета коэффициента корреляции построена таким образом что если связь между признаками имеет линейный характер коэффициент Пирсона точно устанавливает тесноту этой связи Поэтому он называется также коэффициентом линейной корреляции Пирсона Если же связь между переменными Х и Y не линейна то Пирсон предложил для оценки тесноты этой связи так называемое корреляционное отношение (см 11 9)
Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем 1 Эти два числа +1 и -1 — являются границами для коэффициента корреляции Когда при расчете получается величина большая +1 или меньшая -I — следовательно произошла ошибка в вычислениях
Если коэффициент корреляции по модулю оказывается близким к 1 то это соответствует высокому уровню связи между переменными Так в частности при корреляции перемен ной величины с самой собой величина коэффициента корреляции будет равна +1 Подобная связь характеризует прямо пропорциональную зависимость Если же значения переменной X будут распложены в порядке возрастания а те же значения (обозначенные теперь уже как переменная )0 будут располагаться в порядке убывания то в этом случае корреляция между переменными X н У будет равна точно -1 Такая величина коэффициента корреляции характеризует обратно пропорциональную зависимость
Знак коэффициента корреляции очень важен для интерпретации полученной связи Подчеркнем еще раз что если знак коэффициента линейной корреляции — плюс то связь между коррелирующими признаками такова что большей величине одного признака (переменной) соответствует большая величина другого признака (другой переменной) Иными словами, если один показатель (переменная) увеличивается, то соответственно увеличивается и другой показатель (переменная) Такая зависимость носит название прямо пропорциональной зависимости
Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной Такая зависимость носит название обратно пропорциональной зависимости При этом выбор переменной, которой приписывается характер (тенденция) возрастания — произволен Это может быть как переменная X, так и переменная Y Однако гели психолог будет считать, что увеличивается переменная X, то переменная Y будет соответственно уменьшаться, и наоборот Эти положения очень важно четко усвоить для правильной интерпретации полученной корреляционной зависимости
В общем виде формула для подсчета коэффициента корреляции такова
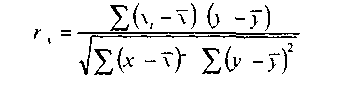
где x1 — значения, принимаемые переменной X,
у1 — значения, принимаемые переменной Y,
х — средняя по X,
у — средняя по Y
Расчет коэффициента корреляции Пирсона предполагает, что переменные Х и У распределены нормально
Формула (111) предполагает, что из каждого значения х переменной X, должно вычитаться ее среднее значение . Это не удобно Поэтому для расчета коэффициента корреляции используют не формулу, а ее аналог, получаемый из простыми преобразованиями
![]()
Где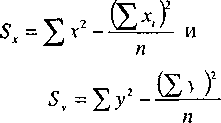
или модификацию этой формулы
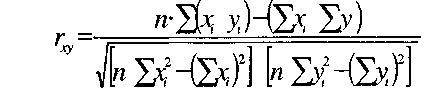
Согласно формулам (11 2а и 11 2Ь) необходимо подсчитать сумму каждой переменной, сумму квадратов каждой переменной и сумму последовательных произведений переменных друг на друга Подчеркнем, что сумма квадратов — не равняется квадрату суммы1 Обратим внимание читателя еще вот на какое обстоятельство В формуле (111) встречается величина
![]()
При делении на я (число значений переменной X или )■) она называется ковариацией Выражение (113) может быть подсчитано только в тех случаях, когда число значений переменной X равно числу значений переменной Y и равно и Формула (113) предполагает также, что при расчете коэффициентов корреля ции нельзя произвольно переставлять элементы в коррелируемых столбцах, как это мы делали, например, в сл>чае расчета по критерию S Джонкиера
Используя формулу 11 2, решим следующую задачу
Задача 20 школьникам были даны тесты на наглядно-образное и вербальное мышление Измерялось среднее время решения задании теста в секундах Психолога интересует вопрос существует ли взаимосвязь между временем решения этих задач0 Переменная X — обозначает среднее время решения наглядно-образных а переменная Y— среднее время решения вербальных заданий тестов.
Решение Представим исходные данные в виде таблицы М2 в которой введены дополнительные столбцы необходимые для расчета по формуле (И 2Ь) В таблице даны индивидуальные значения переменных X и Y построчные произведения переменных Х и У квадраты переменных всех индивидуальных значении переменных X и У а также суммы всех вышеперечисленных величин
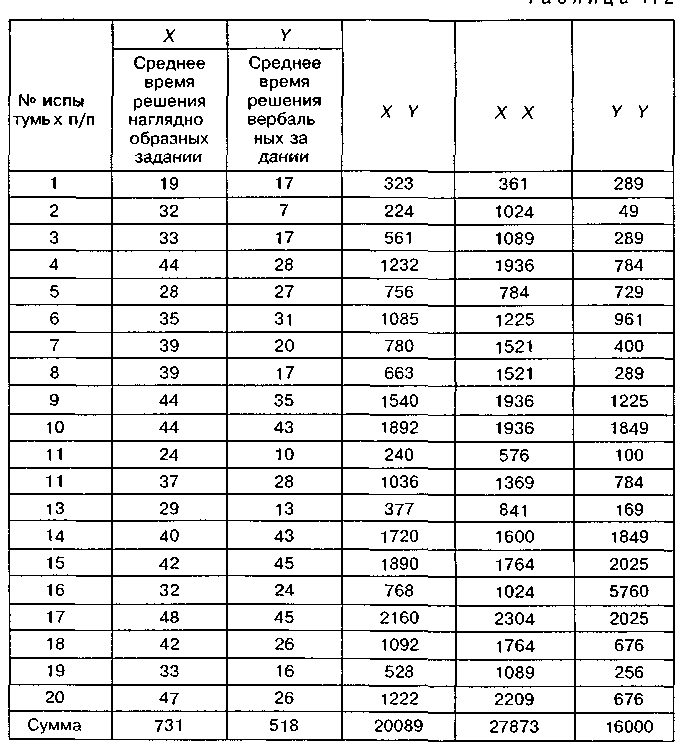
Рассчитываем эмпирическую величину коэффициента корреляции по формуле 1
![]()
Определяем критические значения для полученного коэффициента корреляции по таблице 20 Приложения Особо отметим, что в таблице 20 Приложения величины критических значений коэффициентов линейной корреляции Пирсона даны по абсолютной величине Следовательно, при получении как положительного, так и отрицательного коэффициента корреляции по формуле (11 2) оценка уровня значимости этого коэффициента проводится по той же таблице 20 Приложения без учета знака, а знак добавляется для дальнейшей интерпретации характера связи между переменными Хи Y
При нахождении критических значений для вычисленного коэффициента линейной корреляции Пирсона г )ш число степеней свободы рассчитывается как к = п - 2 В нашем случае к = 20, поэтому «-2 = 20-2=18 В первом столбце таблицы 20 Приложения в строке, обозначенной числом 18, находим
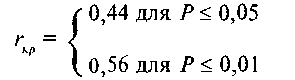
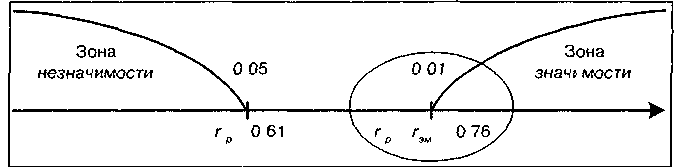
Строим соответствующую ось значимости
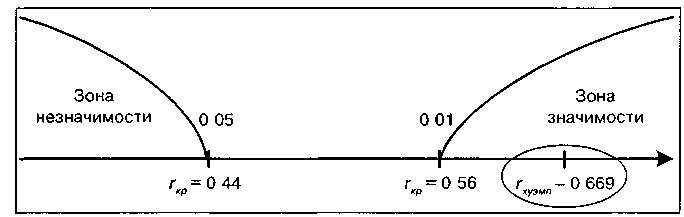
Ввиду того что величина расчетного коэффициента корреляции попала в зону значимости — гипотеза Но отвергается и принимается гипотеза H1. Иными словами, связь между временем решения наглядно образных и вербальных задач статистически значима на 1% уровне и положительна Полученная прямо пропорциональная зависимость говорит о том, что чем выше среднее время решения наглядно-образных задач, тем выше среднее время решения вербальных и наоборот
Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия:
1 Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений
2 Распределения переменных X и Y должны быть близки к нормальному
3 Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым
4 Таблицы уровней значимости для коэффициента корреляции Пирсона (таблица 20 Приложения) рассчитаны от n = 5 до n = 1000 Оценка уровня значимости по таблицам осуществляется при числе степеней свободы к = n – 2
Коэффициент корреляции рангов Спирменв
Коэффициент корреляции рангов, предложенный К Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин Правила ранжирования варьирующих величин были описаны выше (см 14 1)
Величина коэффициента линейной корреляции Спирмена также лежит в интервале +1 и -1 Он, как и коэффициент Пирсона, может быть положительным и отрицательным, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале
В принципе число ранжируемых признаков (качеств, черт и т п ) может быть любым, но сам процесс ранжирования большего чем 20 числа признаков — затруднителен Возможно, что именно поэтому таблица критических значений рангового коэффициента корреляции рассчитана лишь для сорока ранжируемых признаков (и < 40, таблица 21 Приложения 1) В случае использования большего чем 40 числа ранжируемых признаков, уровень значимости коэффициента корреляции следует находить по таблице 20 Приложения для коэффициента корреляции Пирсона Ранговый коэффициент линейной корреляции Спирмена подсчитывается по формуле
![]()
где n— количество ранжируемых признаков (показателей, испытуемых)
∑D — разность между рангами по двум переменным для каждого испытуемого £И — сумма квадратов разностей рангов Используя ранговый коэффициент корреляции, решим следующую задачу
Задача Психолог выясняет, как связаны между собой индивидуальные показатели готовности к школе, полученные до начала обучения в школе у !! первоклассников и их средняя успеваемость в конце учебного года
Решение. Для решения этой задачи были проранжированы, во-первых, значения показателей школьной готовности, полученные при поступлении в школу, и, во-вторых, итоговые показатели успеваемости в конце года у этих же учащихся в среднем Результаты представим в таблице
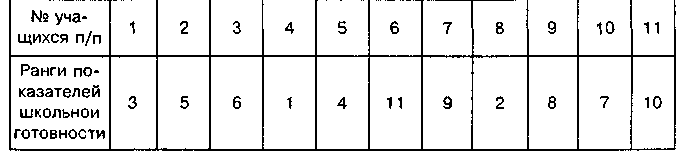
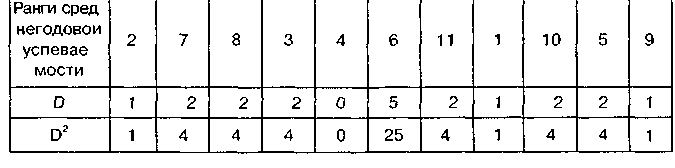
Подставляем полученные данные в формулу (II 4) и производим расчет. Получаем
![]()
Для нахождения уровня значимости обращаемся к таблице 21 Приложения I в которой приведены критические значения для коэффициентов ранговой корреляции Подчеркнем что в таблице 21 Приложения 1 как и в таблице для линейной корреляции Пирсона все величины коэффициентов корреляции даны по абсолютной величине Поэтому еще раз напомним что знак коэффициента корреляции учитывается только при его интерпретации
Однако в отличие от таблицы критических значении пирсоновскои корреляции в таблице 21 Приложения 1 нахождение уровней значимости осуществляется по числу n — те по числу испытуемых В нашем случае n - 11 Для этого числа находим r =0 61 для 0 05 r ~ 0 76 для 0 01 В стандартной форме записи это выглядит следующим образом
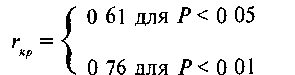
Строим соответствующую ось значимости