
- •1.Основные понятия теории множеств.Объед., пересеч.Св-ва.Nqzrc.Кванторы.
- •3.Функция.Возр, убыв., монотонная, огр сверху, снизу.Огр.Функция.
- •4.Основные элементраные функции.
- •6.Геометрический смысл предела последовательности
- •7.Теорема о единственности предела сходящ.Посл.(док-ть)
- •9.Необходимое усл. Сущ. Предела(с док-вом)
- •10.Беск малые посл-ности.Опр.1-2.
- •12.Произведение беск.Малой посл.На огранич.
- •14.Теорема о пределе суммы 2-х сходящихся последовательностей.
- •18) Предел функции. Определение. Теорема о пределах функции. Геометрический смысл.
- •23. Точки разрыва.
- •41.Формула Лейбница.
- •43) Дифференциал. Определение. Геометрический смысл
- •53) Формула Тейлора.
- •60. Асимптоты кривой. Вертикальные, наклонные. Условия их существования.
6.Геометрический смысл предела последовательности
7.Теорема о единственности предела сходящ.Посл.(док-ть)
Т.Если
посл-ть имеет предел, то он единственный
1)
(
)(
n1;n>n1=>(an-a)<
) 2)
(
)(
n1;n>n1=>(an-b<)<
)
![]()
8.Т.Вейершнасса.достаточн.усл сущ.предела.Если посл-ть монотонно возр и огранич сверху, то она сходится.Если посл-ть монотонно убыв и огранич снизу, то она сходится.
Пример
(![]() =n/(n+1))
– монот возр огр сверху (все члены<1)Она
имеет предел.
=n/(n+1))
– монот возр огр сверху (все члены<1)Она
имеет предел.
( =(2n+3)/n) – монот убыв огр снизу(все члены>0) Она имеет предел.
9.Необходимое усл. Сущ. Предела(с док-вом)
Если
посл. Имеет предел, то такая посл-ность
ограничена.
![]() =>
=>
![]() -огранич.
-огранич.
Док-во: по опр( )( N();n>N=>| -a|<) => , n>N - огранич снизу a- сверху
a+ , m,M a-;a+;m;M выберет max(c) и min (c)=> c< <c => -огранич ч.т.д
10.Беск малые посл-ности.Опр.1-2.
Беск малой посл-ностью, назыв. величина имеющ. своим пределом число 0.
Если посл-ность { } сходится к нулю, то она называется бесконечно малой посл-стью
![]()
![]() св-ва:
св-ва:
1. Сумма бесконечно малых есть бесконечно малая.
2. Произведение бесконечно малых есть бесконечно малая.
3. Произведение бесконечно малой на ограниченную функцию есть бесконечно малая. (Функция f(x) называется ограниченной в точке x=x0, если найдется такое число M и такая -окрестность, что для всех x из -окрестности выполняется неравенство f(x)<M.)
12.Произведение беск.Малой посл.На огранич.
Произв беск малой посл-ти на огранич есть беск малая посл-ность.Из этой теоремы в часности следует, что произведение постоянной величины на беск малую, так же как произвдение нескольких бесконечно малых, является бесконечно малой величиной.Действительно постоянная величина всегда есть величина ограниченная.То же относится и к бесконечно малой.Поэтому, например, произведение двух бесконечно малых можно истолклвать как произведение бесконечно малой на ораниченную.
14.Теорема о пределе суммы 2-х сходящихся последовательностей.
Если посл-ности
и
![]() сходятся, то посл-ность
+
-
тоже сходится и предел суммы этой
посл-ности равен сумме пределов этой
посл-ности.док-во:
сходятся, то посл-ность
+
-
тоже сходится и предел суммы этой
посл-ности равен сумме пределов этой
посл-ности.док-во:
=a+![]() +
=a+b+
+
+
=a+b+
+![]()
![]() =
+
по
т. о сумме малых посл.
=
+
по
т. о сумме малых посл.
=a+
явл. бесконечн малым числом.=>
![]()
18) Предел функции. Определение. Теорема о пределах функции. Геометрический смысл.
 Def:
Def:
![]() на языке
на языке
![]()
![]() - б
- б
Опр. =A
![]()
![]()
Геометрический смысл:
0<![]()
![]()
![]()
22. Непрерывность функции.
Функция f(x) называется непрерывной в точке x=x0, если ее предел в этой точке равен значению функции в этой точке.
Условия непрерывности:

Функция y=f(x) называется непрерывной в
точке x=x0, если она определена в
некоторой окрестности точки x0
(очевидно, и в самой точке x0)и
если![]() или,
что то же самое
или,
что то же самое
![]()
Функция y=f(x) называется непрерывной на данном промежутке, если она непрерывна в каждой точке этого промежутка.
23. Точки разрыва.
Все т-ки разрыва делятся на 3 вида: т.устранимого разрыва, точки р-ва 1и2-го рода.
а) если в т-ке x0 оба односторонних предела, которые совпадают м/д собой
f(x0+0)=f(x00-), но f(x0), то такая точка называется точкой устранимого разрыва.
Если x0 точка устранимого разрыва, то можно перераспределить ф-цию f так чтобы она стала непр. в т-ке x0. Если по ф-ции f построить новую ф-цию положив для нее значен.
f(x0)=f(x0-0)=f(x0+0) и сохр. зн-я в др. т-ках, то получим исправленную f.
б) если в т-ке x0 оба 1-сторонних предела f(x0+0) которые не равны м/д собой
f(x0+0)f(x0-0), то x0 наз-ся т-кой разрыва 1-го рода.
в) если в т-ке x0 хотя бы 1 из односторонних пределов ф-ции не или бесконечен, то x0 наз-ся т-кой раз-ва 2-го рода.
При исследовании сл-е замечания:
1) Все элементарные ф-ции непр-ны во внутренних т-ках своих областей определения при исл. элементарных ф-ций нужно обращать внимание на на граничные т-ки обл. опр.
2) Если ф-ция задана кусочно, т.е. различными соотношениями на частях своей обл. опр., то подозрительными на разрыв явл. граничные т-ки частей обл-ти опр.
26.Замечательные пределы 1,2,3,4.
1)![]() =1
– Читается: предел отношения sin
к его аргументу равен 1-це, когда аргум-т
стремится к 0.
=1
– Читается: предел отношения sin
к его аргументу равен 1-це, когда аргум-т
стремится к 0.
2)
![]() - для после-ти.
- для после-ти.
![]() =
e и
=
e и
![]() - второй зам. предел.
- второй зам. предел.
3)
![]() ;
;
![]() ;.(
;.(![]() -
по непрерыв.)
-
по непрерыв.)
4)![]() ;
Док-ва.
;
Док-ва.
ax-1=z
![]()
ax=z+1

x=loga(1+z)
27) Сравнение Б.м. и Б.б. функций. Б.м. одного порядка, эквивалентные Б.м. и Б.б. более высокого порядка чем другая Б.м.
![]() ;
;![]() - б. малые ф.
- б. малые ф.
1) если
![]()
- бесконечно малая, более высокая порядка чем
2) то говорят что они одного порядка малости
![]()
3) они эквивалентны
![]()
28) Теорема об эквивалентных Б.м. функций. (При вычислении пределов). (Док-ть).
![]()
![]()
![]()
При вычислении пределов произведения и частного можно заменять эквивалентами функции
Док-во:
![]()
При вычислении приделов – нельзя заменять эквивалентами функции.
30.Производная.Определение.Геометр.смысл.Опр.дифф. в точке на множестве.
Производной функции y=f(x) в точке x=0 называется предел отношения приращения
Функции к приращению аргумента при стремлении последнего к 0.
![]() Геометрический смысл состоит в том,
что произв. Ф. в точке есть
Геометрический смысл состоит в том,
что произв. Ф. в точке есть
угловой коэфицент касательной, проведенной к функции в данной точке.
![]() .
Правила диф-ния: если ф.имеет
производн. В точке, то она назыв дифф. в
этой точке.опр:ф.назыв.дифф. в
интервале от a до b,
если она дифференцируема в каждой точке
данного интервала.
.
Правила диф-ния: если ф.имеет
производн. В точке, то она назыв дифф. в
этой точке.опр:ф.назыв.дифф. в
интервале от a до b,
если она дифференцируема в каждой точке
данного интервала.
31.Т.о связи понятий неприрывн. и дифф(необх усл)(доказать)
Пусть y=f(x)
которая дифф. в точке
![]() ,
тогда эта функция будет непрерывна в
этой точке.
,
тогда эта функция будет непрерывна в
этой точке.
Обратная теорема не верна.![]() -
беск.мал.при
-
беск.мал.при
![]() док-во:
док-во:
![]()
![]() непр
в точке
непр
в точке
![]()
![]()
34) Теорема о производной сложной функции. (док-ть).
y=f(x)
z=f(x)
![]()
![]()
Док-во:
![]()
35) Теорема о производной обратной функции. (док-ть).
y=f(x)
x=f(y)
- деференцируем![]()
![]()
Док-во:
![]()
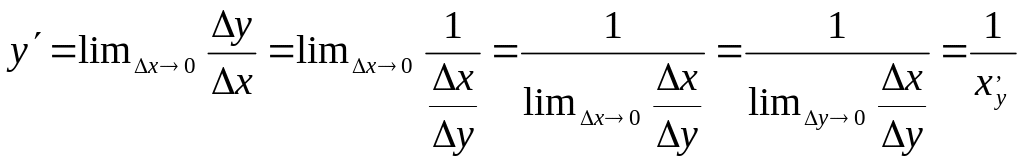
38.Дифференцирование неявн. Фун-ции.
Функ-ция
z=f(x;y)
назыв. неявной, если она задается
уравнением F(x;y;z)=0
(*) неразреш-ым относительно z.
Найдем частные производные
![]() неявной функции z, заданной
уравн-м (*). Для этого подставив в ур-е
вместо z функцию f(x;y),
получим тождество
неявной функции z, заданной
уравн-м (*). Для этого подставив в ур-е
вместо z функцию f(x;y),
получим тождество
F(x;y;f(x;y))0. Частные производные по x и по y функции тождественно равной 0, также равны 0:
![]() F(x;y;f(x;y))=
F(x;y;f(x;y))=![]() (y – считаем постоянным)
(y – считаем постоянным)
![]() F(x;y;f(x;y))=
F(x;y;f(x;y))=
![]() (x – считаем постоянным),
откуда
(x – считаем постоянным),
откуда
![]() и
и
![]() ,
(
,
(![]() )
)
