
Лекція 4.9. Графи
ВСТУП
Теорія графів - одна з небагатьох математичних теорій, для яких точно відомий її засновник, час і місце створення: Леонард Ейлер, 1736 р., м. Петербург. Саме цього року Л.Ейлер в "Записках Петербурзької академії наук" опублікував статтю щодо рішення зараз широко відомої задачі про Кенігсбергські мости. Та робота містила не лише негативну відповідь на питання щодо можливості обійти всі сім мостів м. Кенігсберга так, щоб по кожному з них пройти рівно один раз. У ній також сформульовано й обґрунтовано критерій, за яким на це питання можна відповісти для довільного графа.
Однак ця стаття була єдиною протягом сторіччя. Лише в середині XІX століття відродився інтерес до теорії графів. Дослідження електричних мереж, структур молекул і кристалів, рішення проблем у біології й психології слугували потужним каталізатором у становленні даного розділу математики. Графи виявилися зручним засобом для опису найрізноманітніших систем і ефективним інструментом структурного аналізу. Однією із знаменитіших задач, що спонукала загальний інтерес до теорії графів, була запропонована Де Морганом (близько 1850 р.) проблема чотирьох фарб:
чи досить чотирьох фарб для розфарбування будь-якої карти так, щоб сусідні країни були різного кольору?
Представлення графів
В математиці граф G= <V, E> – кортеж множини вершин V та множини ребер EV×V, кожне з яких задається парою вершин та, можливо, його вартістю.
Орієнтовний граф (або скорочено – орграф) – це граф із спрямованими ребрами, які називають дуги та задають впорядкованими парами вершин, перша з яких є початком, а друга – кінцем дуги.
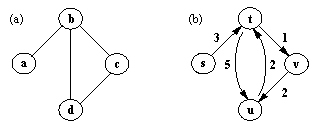
Рис. 1. (а) – неорієнтований, (b) – орієнтований графи
Зазначимо ще, що ребро не зобов'язане з'єднувати різні вершини. Якщо ребро з'єднує вершину саму із собою, то таке ребро називають петлею.
Кількість ребер, що виходять з однієї вершини, називають ступенем цієї вершини. Для петлі будемо вважати, що це ребро виходить із вершини двічі. Ступінь вершини а позначають v(а).
Сформулюємо властивість будь-яких граф.
Теорема 1. Сума ступенів всіх вершин графа дорівнює подвоєному числу його ребер.
Ця теорема доводиться зовсім просто: легко бачити, що, коли підраховується сума ступенів всіх вершин, кожне ребро в цій сумі фігурує рівно два рази.
Наслідком Теореми 1 є "лема про рукостискання".
Теорема 2. Кількість вершин непарного ступеня будь-якого графа завжди парна.
Граф є навантаженим (зваженим), якщо кожне ребро позначене числом (вагою ребра). Залежно від семантики задачі це число може означати відстань або час переходу між вершинами (коли граф зображує якусь транспортну схему), або пропускну здатність каналу між вершинами (якщо граф зображує деяку комунікаційну мережу), або щось іще. Іноді ненавантажений граф доцільно вважати навантаженим із однаковою (число 1) вагою ребер.
У Прологу граф може бути представлений або явно - у вигляді однієї структури, або неявно - набором фактів, що встановлюють наявність ребра (дуги) між вершинами та його вартість (ціле позитивне число).
При явному завданні граф представляється термом у складі списку вершин та списку ребер (заданих бінарним чи тернарним функтором, третій аргумент – вартість дуги чи ребра).
Графи рис.1 можуть бути задані неявно фактами:
(а) – r(a,b).
r(b,d).
r(b,c,).
r(c,d).
(b) – edge(s,t,3).
edge(t,v,1).
edge(t,u,5).
edge(u,t,2).
edge(v,u,2).
а в явній формі – термами:
(а) – graph([a,b,c,d], [r(a,b), r(b,d), r(b,c,), r(c,d)]),
(b) – dgraph([s,t,u,v], [edge(s,t,3), edge(t,v,1), edge(t,u,5), edge(u,t,2), edge(v,u,2)]),
де graph та dgraph – бінарні функтори.
Якщо в графі нема ізольованих вершин (тобто, кожна з них з’єднана хоча б з однією іншою), то в його представленні множину вершин можна опустити, оскільки вона неявно вже є в списку ребер.
Ще один спосіб подання графа - зв'язати з кожною вершиною список суміжних з нею вершин. Тоді граф стає списком пар, кожна з яких складається з вершини та її списку суміжності, наприклад у формі:
G1 = [ a->[b], b->[a, c, d], c->[b, d], d->[b, c]]
G2 = [s->[t/3], t->[u/5, v/l], u->[t/2], v->[u/2]],
де символи '->' та '/' - інфіксні функтори.
На тій же ідеї околиці вершини засноване ще одне практично важливе подання. Граф визначається відношенням neighborhood(A,NB), що зв'язує вершину зі списком її сусідів. Подібним чином представляють граф, розфарбовуючи карту. Неважко визначити процедури, що дозволяють переходити від одного подання до іншого.
edge(A,B):- neighborhood(A,NB),member(B,NB).
neighborhood(A,NB):- setof(B,edge(A,B),NB).
Практично завжди треба визначитись, є оброблюваний граф орієнтованим чи ні.
Яка із наведених форм представлення графів є ефективнішою, залежить від додатку та від операцій, виконуваних над графами. Серед типових операцій:
пошук шляху між двома заданими вершинами;
пошук підграфа, що має деякі задані властивості.
наявність зв'язку між вершинами графа
Дві вершини графа зв'язані, якщо існує послідовність ребер (дуг), що веде з першої вершини в другу.
Постановка 1.
Використаємо неявне подання стосовно до графа:

domains
top=symbol
predicates
edge (top, top) % аргументи позначають імена вершин
path(top,top) % дві вершини зв'язані, якщо між ними
існує шлях.
clauses
edge (a, b).
edge (c, d).
edge (a, c).
edge (d, e).
edge (b, d).
edge (f, g).
path (X, X).
path (X, Y):- edge (X, Z), path (Z, Y).
Постановка 2.
Попередня задача при явній формі представлення графа двома списками: вершин і ребер. Ребро представляється структурою edge.
domains
edge= e(symbol, symbol) % аргументи - імена вершин
list1=symbol*
list2=edge*
graf = g(list1, list2)
predicates
path(graf, symbol, symbol) % відношення зв'язаності
вершин у графі
clauses
path (g([],[]),_,_).
path (g([X|_],[e(X,Y)|_]),X,Y).
path (g([X|T],[e(X,_)|T1]),X,Y):-
path (g([X|T],T1),X,Y).
path (g([X|T],[e(_, _)|T1]),X,Y):-
path (g([X|T],T1),X,Y).
path (g([X|T],[e(X,Z)|T1]),X,Y):-
path (g([X|T],T1),Z,Y).
goal
path (g([a, b, c, d],[e(a, b),e(b, c),e(a, d),e(c, b)]), a, c).
Пошук шляху на графі.
Шлях – це послідовність вершин, з'єднаних дугами. Для орграфа напрямок шляху має збігатись з напрямком кожної дуги шляху.
Цикл – це шлях, у якого збігаються початок і кінець.
Програми пошуку шляху на графі належать до недетермінованих програм з невідомим вибором альтернативи, оскільки в них невідомо, яке з рекурсивних правил буде виконано в процесі доказу, аж до успішного завершення обчислень. Такі програми є специфікацією алгоритму пошуку в глибину для розв'язку певної задачі.
Постановка 3.
Визначити шлях P між вершинами A та B графа, заданого неявно:
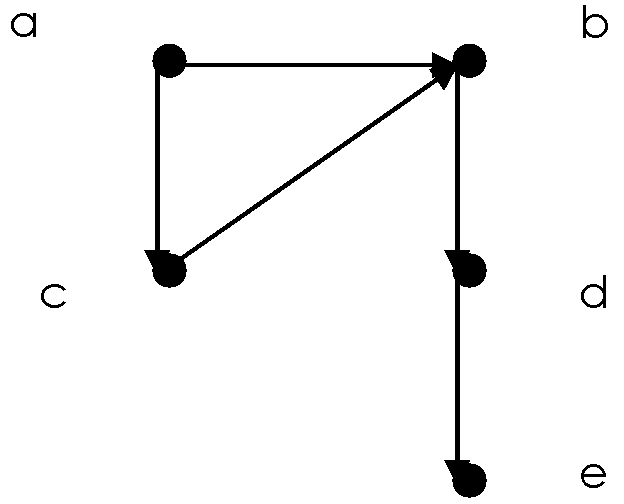
A – початок шляху;
B – кінець шляху;
P – ациклічний (не має повторів вершин) шлях на графі.
domains
top=symbol
listtop=top*
predicates
edge (top, top) % аргументи позначають імена вершин
path (top, top, listtop) %формує список вершин шляху
clauses
edge (a, b).
edge (b, c).
edge (c, a).
edge (b, d).
edge (d, e).
path (A, A, [A]).
path (A, B, [A|P]):-edge(A, N), path(N, B, P).
Згідно цього визначення за допомогою пошуку в глибину здійснюється коректний обхід будь-якого скінченого дерева або ациклічного графа, заданого у неявній формі (подібно до прикладу).
Більш складними є задачі обходу графа із циклами, в яких можливий нескінченний програмний цикл по одному із циклів графа. Позбутись зациклення програми можна:
обмеженням на глибину пошуку або
накопиченням пройдених вершин.
Останній спосіб забезпечує виключення повторного використання пройдених вершин, накопичених у додатковому аргументі відношення path.
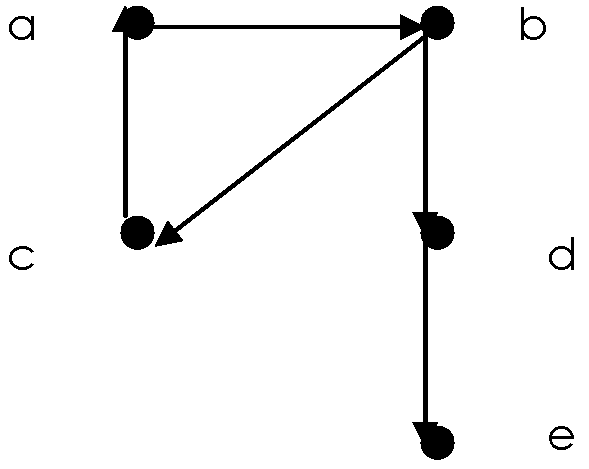
Постановка 4.
Шлях у заданому неявно скінченому орграфі:
domains
top=symbol
listtop=top*
predicates
edge(top,top)
path (top,top,listtop,listtop)
path (top,top)
member(top,listtop)
reverse(listtop,listtop,listtop)
clauses
edge(a,b).
edge(b,c).
edge(c,a).
edge(b,d).
edge(d,e).
member(A,[A|_]):-!.
member(A,[_|T]):-member(A,T).
reverse([],T2,T2).
reverse([H|T],T1,T2):-reverse(T,[H|T1],T2).
path(A,B,P,[B|P]):-edge(A,B).
path(A,B,P,P2):-edge(A,N),not(member(N,P)),
P1=[N|P], path (N,B,P1,P2).
path(A,B):-
path(A,B,[A],P),reverse(P,[],Res),write(Res).
goal
path(a,e).
У цій програмі предикат path(A,B,[A],P) відшукує шлях в оберненому вигляді, тобто спочатку йде остання вершина, а наприкінці – перша. Використання ж предиката reverse(P,[],Res) відновлює порядок відвідань вершин.
Постановка 4.1.
Шлях у зваженому неорієнтованому графі, заданому неявно:

domains
slist=string*
predicates
edge(string,string,integer).
e(string,string,integer).
path(string,string,slist).
p(string,slist,slist).
member(string,slist).
clauses
edge(a,c,8).
edge(a, b, 3).
edge(c, d, 12).
edge(b, d, 0).
edge(e, d, 9).
e(A,B,C):-edge(A,B,C);edge(B,A,C).
path(A,B,P):-p(A,[B],P). % шукаємо шлях від кінцевої
вершини в початкову.
Початковий шлях включає
лише кінцеву вершину
p(A,[A|Tail],[A|Tail]). % якщо поточна вершина
шляху є початковою, то
цей шлях є шуканим
p(A,[B|Tail],P) :- e(B,C,_), not(member(C,Tail)),
p(A,[C,B|Tail],P). % B - поточна вершина шляху.
Відшукуємо вершину С, в яку
є шлях з В і якої ще нема у
шляху, та пробуємо знайти
шлях (від цієї нової вершини
С) до початкової вершини А
Постановка 5.
Ациклічний шлях Р між вершинами А і Z у заданому явно графі G позначимо відношенням path(А, Z, G, Р).
Для графа G на рис. 1 (а) вірними є твердження:
path( a, d, G, [a, b, d] )
path( а, d, G, [a, b, c, d] ).
Оскільки шлях має бути ациклічним, всяка вершина у шляху може зустрітись лише раз. Один з методів пошуку шляху відповідно до предикату path(А, Z, G, Р):
якщо А=Z, то покласти шлях Р= [А],
інакше знайти ациклічний шлях Р1 з довільної вершини Y в вершину Z, а потім шлях з А в Y без використання вершин з шляху Р1.
Для цього визначено ще один предикат:
path1(А, Р1, G, Р)
чиї аргументи мають наступний смисл:
А - деяка вершина,
P1 - шлях в G,
G - граф,
Р - ациклічний шлях в G, що йде з А в початкову вершину шляху Р1, а потім - уздовж шляху Р1.
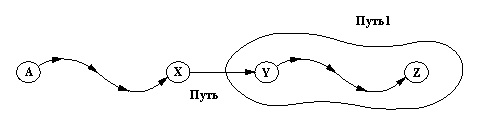
Pис. 3. Відношення path фіксує шлях Р між А і Z, що у своїй заключній частині співпадає зі шляхом Р1 між вершинами Y і Z відношення path1.
Між path і path1 має місце наступне співвідношення:
path(А, Z, G, Р) :- path1( А, [Z], G, Р).
На рис.3 показана ідея рекурсивного визначення відношення path1. Існує "граничний" випадок, коли початкова вершина шляху P1 (Y на рис. 3) збігається з початковою вершиною А шляху Р. Якщо ж початкові вершини цих двох шляхів не збігаються, то має існувати така вершина X, що
(1) Y - вершина, суміжна з X,
(2) Х не втримується в Р1 та
(3) для Р виконується відношення
path1( А, [Х | Р1], G, Р).
Таким чином, пошук у графі G ациклічного шляху Р з вершини А в Z визначається наступною програмою:
path( A, Z, G, Р) :- path1( А, [Z], G, Р).
path1( А, [А | Р1], _, [А | Р1] ).
path1( А, [Y | Р1], G, Р) :- incident( X, Y, G),
not(member(X, Р1)), % Умова відсутності циклу
path1( А, [ X, Y | Р1], G, Р).
Тут відношення інцидентності (суміжності) вершин
