13. Измерение углов на местности

И змерение углов на местности проводится с помощью специальных при­боров. Простейшим из них является аст­ролябия (рис. 36). Она состоит из двух ча­стей: диска, разделенного на градусы, и вращающейся вокруг центра диска линей­ки (алидады). На концах алидады находят­ся два узких окошечка, которые исполь­зуются для установки ее в определенном направлении.

Измерения углов проводятся в различных исследованиях, например в аст­рономии при определении положения небес­ных тел. Очень важно с достаточной точно­стью измерять углы при определении поло­жения искусственных спутников на орби­тах. Для этой цели конструируют специаль­ные приборы.

14. Смежные и вертикальные углы

Два угла, у которых одна сторона общая, а две другие являются продолжения­ми одна другой, называются смежными.

Н а рисунке 40 углы АОВ и ВОС смежные. Так как лучи ОА и ОС образуют развернутый угол, то

AOB+BOC = AOC = 180°.

Таким образом свойство смежных углов, сумма смежных углов равна 180°.

Два угла называются вертикаль­ными, если стороны одного угла являются продолжениями сторон другого.

Н а рисунке 41 углы 1 и 3, а также углы 2 и 4 — вертикальные.

Угол 2 является смежным как с уг­лом 1, так и с углом 3. По свойству смежных углов l+2 = 180° и 3+2 = 180°.

Отсюда получаем: l = 180° - 2, 3 = 180° - 2. Та­ким образом, градусные меры углов 1 и 3 равны. Отсюда следует, что и сами углы рав­ны. Итак, вертикальные углы равны.

15. Перпендикулярные прямые

Р ассмотрим две пересекающиеся прямые (рис. 42). Они образуют четыре не­развернутых угла. Если один из них пря­мой (угол 1 на рис. 42), то остальные углы также прямые (объясните почему).

Две пересекающиеся прямые назы­ваются перпендикулярными (или взаимно перпендикулярными), если они образуют че­тыре прямых угла.

Перпендикулярность прямых АС и BD обозначается так: ACBD (читается: «Пря­мая АС перпендикулярна к прямой BD»).

Отметим, что две прямые, пер­пендикулярные к третьей, не пересе­каются (рис. 43, а).

В самом деле, рассмотрим прямые АА₁ и BB₁ перпендикулярные к прямой PQ (рис. 43, б). Мысленно перегнем рисунок по прямой PQ так, чтобы верхняя часть рисун­ка наложилась на нижнюю. Так как пря­мые углы 1 и 2 равны, то луч РА наложится на луч PA₁ Аналогично, луч QB наложится на луч QB₁. Поэтому, если предположить, что прямые АА₁ и ВВ₁ пересекаются в точке М, то эта точка наложится на некоторую точку M₁ также лежащую на этих прямых (рис. 43, в), и мы получим, что через точки М и М₁ проходят две прямые: АА₁ и BB₁. Но это невозможно. Следовательно, наше пред­положение неверно и, значит, прямые АА₁ и ВВ₁ не пересекаются.

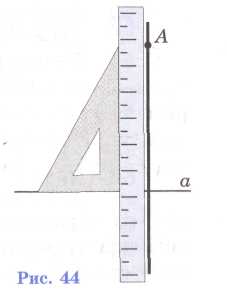
Для проведения перпендикуляр­ных прямых используют чертежный уголь­ник и линейку (рис. 44).

16. Треугольник

Отметим какие-нибудь три точки, не лежащие на одной прямой, и соединим их отрезками (рис. 49, а). Получим геомет­рическую фигуру, которая называется тре­угольником. Отмеченные три точки называ­ются вершинами, а отрезки — сторонами треугольника. На рисунке 49, б изображен треугольник с вершинами А, В, С и сторона­ми АВ, ВС и СА. Такой треугольник будем обозначать так: ∆ АВС (читается: «треуголь­ник ABC»). Этот же треугольник можно обо­значить иначе, записав буквы А, В, С в дру­гом порядке: ∆ ВСА, ∆ СВА и т. д.

Три угла— BAC, CBA и ACB — называются углами треугольника АВС. Часто их обозначают одной буквой: A, B, C.

Сумма длин трех сторон треуголь­ника называется его периметром.

Напомним, что две фигуры, в ча­стности два треугольника, называются рав­ными, если их можно совместить наложе­нием. На рисунке 50 изображены равные треугольники АВС и А₁В₁С₁.

Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совме­стятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.

Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.

Отметим, что в равных треуголь­никах против соответственно равных сторон, (совмещающихся при наложении) лежат равные углы, и обратно: против со­ответственно равных углов лежат равные стороны. Так, например, в равных треуголь­никах ABC и А₁В₁С₁ изображенных на ри­сунке 50, против соответственно равных сто­рон АВ и А₁В₁ лежат равные углы С и С₁.

Равенство треугольников ABC и А₁В₁С₁ обозначается так:

∆АВС= ∆А₁В₁С₁.