Аксиоматика по Погорелову.Проверка Аксиом принадлежности и параллельных

Министерство образования и науки Российской Федерации

Пермский государственный педагогический университет

Реферат

Аксиоматика евклидового пространства по Погорелову

и ее противоречивость.

Список аксиом евклидовой планиметрии.

Построение арифметической модели.

Проверка аксиом принадлежности и параллельности.

Выполнила ст. ОЗО МФ: Попова Е.А.

Проверил преподаватель: Панкратова Л.Я.

Пермь

2009

Аксиоматика евклидового пространства по Погорелову.

Основными понятиями в нашем изложении будут точка, прямая и плоскость, отношение принадлежности для точек, прямых и плоскостей, выражаемое словом «принадлежать», отношение порядка для точек на прямой, выражаемое словами «лежать между», «длина» для отрезков и «градусная мера» для углов. Эти понятия не определяются и все, что о них предполагается известным, выражается аксиомами.

По соображениям удобства изложения мы сначала сформулируем плоские аксиомы. А затем введем группу пространственных аксиом С. Плоские аксиомы естесственно разбиты на группы в соответствии с основными понятиями: принадлежности, порядка и меры.

Аксиомы принадлежности.

Аксиомы принадлежности определяют свойства взаимного расположения точек и прямых.

Если точка принадлежит двум прямым, то мы говорим, что прямые пересекаются в этой точке, или эта точка является точкой пересечения прямых.

Группа аксиом принадлежности включает следующие две аксиомы:

Аксиома . Каковы бы ни были две точки, существует прямая, проходящая через эти точки, и притом только одна.

Аксиома . На каждой прямой лежат по крайней мере две точки. Существует три точки, не лежащие на одной прямой.

Следствие аксиомы . Две прямые либо не пересекаются, либо пересекаются только в одной точке.

Следствие аксиомы . Какова бы ни была прямая, существует точка, не лежащая на этой прямой.

Аксиомы порядка.

Аксиомы порядка выражают свойства взаимного расположения точек на прямой и на плоскости. При этом используется отношение взаимного расположения точек на прямой, выражаемое словами «лежать между».

Аксиома . Из трех точек на прямой одна и только одна лежит между двумя другими.

Аксиома . Прямая разбивает множество не принадлежащих ей точек плоскости на два подмножества (полуплоскости) так, что отрезок, соединяющий точки одной полуплоскости, не пересекается с прямой, а отрезок, соединяющий точки разных полуплоскостей, пересекается с прямой.

Следствие аксиомы . Если прямая, не проходящая ни через одну из вершин треугольника, пересекается одну из его сторон, то она пересекает, и притом только одну, из двух других сторон.

Аксиомы меры для отрезков и углов.

Аксиома . Каждый отрезок имеет определенную длину, большую 0. Если точка С лежит на отрезке АВ, то длина отрезка АВ равна сумме длин отрезков АС и ВС: .

Аксиома позволяет ввести координату на прямой, т.е. сопоставить каждой точке прямой вещественное число так, что если и - координаты точек А и В, то длина отрезка .

Аксиома . Кажый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180˚. Если луч с проходит между сторонами угла (ab), то градусная мера угла (ab) равна сумме градусных мер углов (ac) и (bc).

Отметим следующую теорему:

Если от полупрямой a отложить в одну полуплоскость относительно этой полупрямой и ее продолжения углы (ab) и (aс), то либо луч с проходит между сторонами угла (ab), либо луч b проходит между сторонами угла (aс). В любом случае .

Аксиома существования треугольника, равного данному.

Аксиома . Пусть и а – полупрямая. Тогда существует , у которого вершина совпадает с началом луча а, вершина лежит на луче а, вершина лежит в заданной полуплоскости относительно прямой, содержащей луч а.

Следствия аксиомы .

1. На данной полупрямой из ее начальной точки можно отложить отрезок, равный данному отрезку, и притом только один.

2. От данной полупрямой в данную полуплоскость, определяемую этой полупрямой и ее продолжением, можно отложить угол, равный данному углу, и притом только один.

Аксиомы существования отрезка данной длины.

Аксиома . Каково бы ни было вещественное число d > 0, существует отрезок длиной d.

Следствия аксиомы .

1. На любой полупрямой из ее начальной точки можно отложить отрезок любой заданной длины, и при том только один.

2. Введением координат на прямой устанавливается взаимнооднозначное соответствие между точками прямой и вещественными числами.

Отметим следующую теорему:

Каково бы ни было положительное число , от данной полупрямой а в заданную полуплоскость можно отложить, и притом только один, угол (ab) с градусной мерой .

Аксиома параллельных.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Аксиома . Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельную данной.

Следствия аксиомы .

1. Свойство параллельности прямых транзитивно: и , то .

2. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Пространственные аксиомы.

Аксиома . Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

Аксиома . Если две различные плоскости имеют общую точку, то они пересекаются по прямой.

Аксиома . Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Отметим несколько следствий:

1. Через прямую и не лежащую на ней точку можно провести плоскость, и при том только одну.

2. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

3. Через три точки, не лежащие на прямой, можно провести плоскость, и притом только одну.

Непротиворечивость аксиоматики по Погорелову.

Проверка аксиом принадлежности и параллельности.

Основные понятия.

Точкой мы будем называть любую пару вещественных чисел х и у, взятых в определенном порядке (х, у), а эти числа будем называть координатами точки.

Прямой мы будем называть совокупность всех точек, координаты которых удовлетворяют линейному уравнению , причем . Это уравнение будем называть уравнением прямой. Прямые и будем называть осями координат, а точку (0,0) началом координат.

Мы будем говорить, что точка принадлежит прямой, если она является одной из ее точек, т.е. ее координаты удовлетворяют уравнению прямой.

Для установления непротиворечивости данной аксиоматики достаточно построить модель евклидового пространства в рамках надежной теории, где бы выполнялись все вышеперечисленные аксиомы. В качестве надежной теории возьмем арифметику.

Покажем, что при таком конкретном понимании основных понятий, для них выполняются аксиомы принадлежности и параллельности.

Аксиомой утверждается, что через две точки можно провести прямую, и притом только одну. Эта аксиома выполняется. Действительно, пусть и - данные точки. Прямая, задаваемая уравнением проходит через данные точки, т.к. их координаты удовлетворяют этому уравнению. Докажем, что прямая единственная. Допустим, через точки и продят две прямые: , . Так как система из этих двух уравнений имеет два решения и , то уравнения зависимы, т.е. отличаются только множителем. А это значит – прямые совпадают.

Аксиомой утверждается, что на каждой прямой лежат по крайней мере две точки, и существуют три точки, не лежащие на прямой.

- Покажем, что эта аксиома выполняется. Действительно, пусть - уравнение прямой. Тогда по крайней мере один из коэффициентов или отличен от нуля, например, . Возьмем произвольные числа и () и найдем числа и по формулам и . Точки () и () лежат на нашей прямой.

- Докажем существование трех точек, не лежащих на одной прямой. Возьмем точки (0,0), (0,1), (1,0). Эти три точки не лежат на одной прямой. Действительно, допустим, они лежат на некоторой прямой . Подставляя координаты точек в уравнение прямой, последовательно получаем , , . Но ведь . Мы пришли к противоречию. Утверждение доказано.

Проверим выполнимость аксиомы параллельных. Докажем, что через точку , лежащую вне прямой , можно провести не более одной прямой, ей параллельной. Допустим, существуют две такие прямые и , проходящие через точку и параллельные данной прямой, т.е. не пересекающие ее. Составим системы:

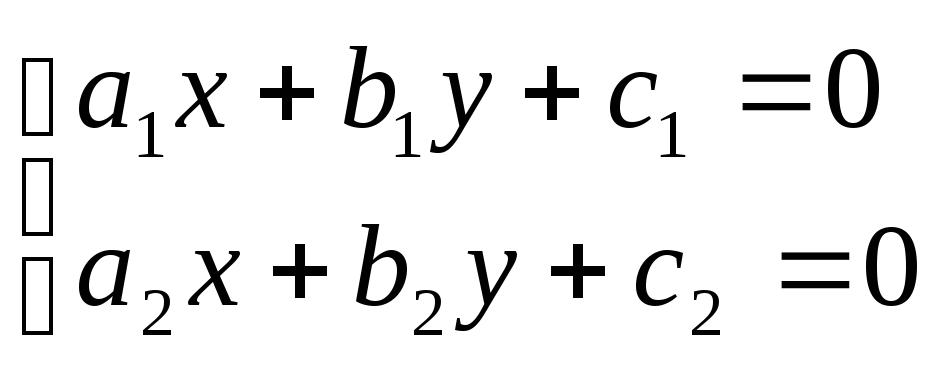Обе системы не совместны, т.е. не имеют решений. Поэтому , . Отсюда , и так как система имеет решение , то ее уравнения зависимы, т.е. отличаются только множителем. А это значит, что прямые совпадают вопреки предположению. Итак, выполнимость аксиомы доказана.

Аналогично проверяется выполнимость остальных аксиом.

Вывод: в построенной модели выполняются все аксиомы, следовательно аксиоматика евклидового пространства непротиворечива, если непротиворечива арифметика.