Абсолютные показатели вариации включают:

• размах вариации 

• среднее линейное отклонение 

• дисперсию 

• среднее квадратическое отклонение 

Размах вариации — это разность между максимальным и минимальным значениями признака

Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.

Среднее линейное отклонение  — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.

Среднее линейное отклонение простое:

Среднее линейное отклонение взвешенное применяется для сгруппированных данных:

Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).

Дисперсия - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

Дисперсия простая:

Дисперсия взвешенная:

Более удобно вычислять дисперсию по формуле:

которая получается из основной путем несложных преобразований. 

Среднее квадратическое отклонение  равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической.

Для подробного описания особенностей распределения использу­ются дополнительные характеристики, в частности, определяются мо­менты распределения.

Моментом k-го порядка называется средняя из k-x степеней от­клонений вариантов х от некоторой постоянной величины А:

При использовании в каче­стве весов частот или частостей моменты называются эмпирически­ми, а при использовании вероятностей — теоретическими.

Показатели формы распределения.

Выяснение общего характера распределения предполагает оценку его однородности, а также расчет показателей асимметрии и эксцесса.

При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии:

Его величина может быть положительной (для правосторонней асимметрии) и отрицательной (для левосторонней асимметрии).

Применение данного показателя дает возможность определить не только величину асимметрии, но и проверить ее наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной. Если асимметрия меньше 0,25, она считается незначительной.

Наличие асимметрии в генеральной совокупности проверяется с помощью определения оценки существенности на основе средней квадратической ошибки:

В случае, если , асимметрия считается существенной и распределение признака в генеральной совокупности несимметрично и неслучайно, а закономерно.

Для симметричных распределений может быть рассчитан показатель эксцесса, который показывает, насколько резкий скачок имеет изучаемое явление. Показатель эксцесса определяется на основе центрального момента четвертого порядка по формуле:

Если показатель эксцесса больше нуля, то распределение островершинное и скачок считается значительным, если коэффициент эксцесса меньше нуля, то распределение считается плосковершинным и скачок считается незначительным. Среднеквадратическая ошибка эксцесса показывает, насколько существенен скачок в явлении и рассчитывается по формуле:

6. Дисперсионный анализ.

Дисперсионный анализ (от латинского Dispersio – рассеивание / на английском Analysis Of Variance - ANOVA) применяется для исследования влияния одной или нескольких качественных переменных (факторов) на одну зависимую количественную переменную.

В основе дисперсионного анализа лежит предположение о том, что одни переменные могут рассматриваться как причины (факторы, независимые переменные): , а другие как следствия (зависимые переменные). Независимые переменные называют иногда регулируемыми факторами именно потому, что в эксперименте исследователь имеет возможность варьировать ими и анализировать получающийся результат.

Основной целью дисперсионного анализа (ANOVA) является исследование значимости различия между средними с помощью сравнения (анализа) дисперсий. Разделение общей дисперсии на несколько источников, позволяет сравнить дисперсию, вызванную различием между группами, с дисперсией, вызванной внутригрупповой изменчивостью. При истинности нулевой гипотезы (о равенстве средних в нескольких группах наблюдений, выбранных из генеральной совокупности), оценка дисперсии, связанной с внутригрупповой изменчивостью, должна быть близкой к оценке межгрупповой дисперсии. Если вы просто сравниваете средние в двух выборках, дисперсионный анализ даст тот же результат, что и обычный t-критерий для независимых выборок (если сравниваются две независимые группы объектов или наблюдений) или t-критерий для зависимых выборок (если сравниваются две переменные на одном и том же множестве объектов или наблюдений).

Сущность дисперсионного анализа заключается в расчленении общей дисперсии изучаемого признака на отдельные компо­ненты, обусловленные влиянием конкретных факторов, и проверке гипотез о значимости влияния этих факторов на исследуемый признак. Сравнивая компоненты дисперсии друг с другом посредством F—критерия Фишера, можно определить, какая доля общей вариативности результативного признака обусловлена действием регулируемых факторов.

Исходным материалом для дисперсионного анализа служат данные исследования трех и более выборок: , которые могут быть как равными, так и неравными по численности, как связными, так и несвязными. По количеству выявляемых регулируемых факторов дисперсионный анализ может бытьоднофакторным (при этом изучается влияние одного фактора на результаты эксперимента), двухфакторным (при изучении влияния двух факторов) и многофакторным (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие).

Дисперсионный анализ относится к группе параметрических методов и поэтому его следует применять только тогда, когда доказано, что распределение является нормальным.

Дисперсионный анализ используют, если зависимая переменная измеряется в шкале отношений, интервалов или порядка, а влияющие переменные имеют нечисловую природу (шкала наименований).

6. Выравнивание вариационных рядов. Теоретические распределения. Распределения Гаусса и Пуассона.

Практически все ряды динамики экономических показателей на графике имеют форму кривой, ломаной линии с подъемами и снижениями. Во многих случаях по фактическим данным ряда динамики и по графику трудно определить даже общую тенденцию развития. Но статистика должна не только определить общую тенденцию развития явления (рост или снижение), но и дать количественные (цифровые) характеристики развития.

Тенденции развития явлений изучают методами выравнивания рядов динамики:

• Метод укрупнения интервалов

• Метод скользящей средней

• Метод аналитического выравнивания

Метод укрупнения интервалов времени основан на исчислении средних величин за укрупненные периоды времени. Цель — абстрагироваться от влияния случайных факторов, взаимопогасить их влияние в отдельные годы.

Метод скользящей средней также основан на исчислении средних величин за укрупненные периоды времени. Цель та же — абстрагироваться от влияния случайных факторов, взаимопогасить их влияние в отдельные годы. Но метод расчета другой.

Метод аналитического выравнивания основан на вычислении значений выравненного ряда по соответствующим математическим формулам. вычисления по уравнению прямой линии:

Под теоретической кривой распределения понимается графическое изображение ряда в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариантов (значений признака). Теоретическое распределение может быть выражено аналитически – формулой, которая связывает частоты вариационного ряда и соответствующие значения признака. Такие алгебраические формулы носят название законов распределения. График нормального распределения имеет форму колоколообразной кривой, симметричной относительно, концы которой асимптотически приближаются к оси абсцисс. Она имеет точки перегиба, абсциссы которых находятся на расстоянии s от центра симметрии. Эта кривая выражается уравнением: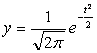

где у – ордината кривой нормального распределения; - нормированные отклонения.

 -2s        -s        +s     +2s  Рис. Кривая нормального распределения

Закон Пуассона. Другое название его – закон ра-определения редких событий. Закон Пуассона (З. П.) применяется в тех случаях, когда маловероятно, и поэтому применение Б/З/Р нецелесообразно.

Достоинствами закона являются: удобство при вычислении, возможность вычислить вероятность в заданном промежутке времени, возможность замены времени другой непрерывной величиной, например, линейными размерами.

Закон Пуассона имеет следующий вид:

и читается следующим образом: вероятность появления события А в m раз при n независимых испытаниях выражается формулой вида (59), где а = пр – среднее значение p(A), причем а является единственным параметром в законе Пуассона.

Закон нормального распределения (закон Гаусса). Практика неуклонно подтверждает, что закону Гаусса с достаточным приближением подчиняются законы распределения ошибок при измерениях самых различных параметров: от линейных и угловых размеров до характеристик основных механических свойств стали.

Плотность вероятности закона нормального распределения (в дальнейшем Н. Р.) имеет вид

где x0 – среднее значение случайной величины;

? – среднее квадратическое отклонение той же случайной величины;

e = 2,1783... – основание натурального логарифма;

Ж – параметр, который удовлетворяет условию.

Причина широкого применения закона нормального распределения теоретически определяется теоремой Ляпунова.

При известных Х0 и ? ординаты кривой функции f(x) можно вычислить по формуле

где t – нормированная переменная,

(t) плотность вероятности z. Если подставить z и (t) в формулу, то следует:

Кривую З.Н.Р. часто называют кривой Гаусса, этот закон описывает очень многие явления в природе.

6. Критерии согласия эмпирического и теоретического распределений.

Эмпирические частоты получают в результате опыта (наблюдения). Теоретические частоты рассчитывают по формулам. Так как все предположения о характере того или иного распределения – это гипотезы, то они должны быть подвергнуты статистической проверке с помощью критериев согласия, которые дают возможность установить, когда расхождения между теоретическими и эмпирическими частотами следует признать несущественными, т.е. случайными, а когда – существенными (неслучайными).

Критерий согласия Пирсона – один из основных:где k – число групп, на которые разбито эмпирическое распределение,  – наблюдаемая частота признака в i-й группе,– теоретическая частота. Для распределения составлены таблицы, где указано критическое значение критерия согласия для выбранного уровня значимости и степеней свободы df.(или ) Уровень значимости – вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. В статистике пользуются тремя уровнями:

• a= 0,10, тогда Р=0,90 (в 10 случаях их 100 может быть отвергнута правильная гипотеза);

• a= 0,05, тогда Р=0,95;

• a= 0,01, тогда Р=0,99.

Число степеней свободы df определяется как число групп в ряду распределения минус число связей: df = k –z.  Под числом связей понимается число показателей эмпирического ряда, использованных при вычислении теоретических частот, т.е. показателей, связывающих эмпирические и теоретические частоты. Например, при выравнивании по кривой нормального распределения имеется три связи: ; ;  . Поэтому при выравнивании по кривой нормального распределения число степеней свободы определяется как df = k –3.   Для оценки существенности расчетное значение сравнивается с табличным . При полном совпадении теоретического и эмпирического распределений , в противном случае >0. Если >, то при заданном уровне значимости и числе степеней свободы гипотезу о несущественности (случайности) расхождений отклоняем.  В случае, если , заключаем, что эмпирический ряд хорошо согласуется с гипотезой о предполагаемом распределении и с вероятностью Р=(1-a) можно утверждать, что расхождение между теоретическими и эмпирическими частотами случайно. Критерий согласия Пирсона используется, если объем совокупности достаточно велик , при этом частота каждой группы должна быть не менее 5.

Критерий Романовского с основан на использовании критерия Пирсона,  т.е.  уже найденных значений , и числа степеней свободы df:

Он удобен при отсутствии таблиц для . Если с<3, то расхождения распределений случайны, если же с>3, то не случайны и теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.

 Критерий Колмогорова l основан на определении максимального расхождения между накопленными частотами и частостями эмпирических и теоретических распределений: или , где D и d – соответственно максимальная разность между накопленными частотами и накопленными частостями эмпирического и теоретического рядов распределений; N          – число единиц совокупности. Рассчитав значение l, по таблице Р(l) определяют вероятность, с которой можно утверждать, что отклонения эмпирических частот от теоретических случайны. Вероятность Р(l) может изменяться от 0 до 1. При Р(l)=1 происходит полное совпадение частот, Р(l)=0 – полное расхождение. Если l принимает значения до 0,3, то Р(l)=1. Основное условие использования критерия Колмогорова – достаточно большое число наблюдений.

6. Выборочное наблюдение. Ошибки выборки. Повторная и бесповторная выборки. Большая и малая выборки.

По способу отбора (способу формирования) выборки единиц из генеральной совокупности распространены следующие виды выборочного наблюдения:

• простая случайная выборка (собственно-случайная);

• типическая (стратифицированная);

• серийная (гнездовая);

• механическая;

• комбинированная;

• ступенчатая.

Простая случайная выборка (собственно-случайная) есть отбор единиц из генеральной совокупности путем случайного отбора, но при условии вероятности выбора любой единицы из генеральной совокупности. Отбор проводится методом жеребьевки или по таблице случайных чисел.

Типическая (стратифицированная) выборка предполагает разделение неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц.

Для серийной (гнездовой) выборки характерно то, что генеральная совокупность первоначально разбивается на определенные равновеликие или неравновеликие серии (единицы внутри серий связаны по определенному признаку), из которых путем случайного отбора отбираются серии и затем внутри отобранных серий проводится сплошное наблюдение.

Механическая выборка представляет собой отбор единиц через равные промежутки (по алфавиту, через временные промежутки, по пространственному способу и т.д.). При проведении механического отбора генеральная совокупность разбивается на равные по численности группы, из которых затем отбирается по одной единице.

Комбинированная выборка основана на сочетании нескольких способов выборки.

Многоступенчатая выборка есть образование внутри генеральной совокупности вначале крупных групп единиц, из которых образуются группы, меньшие по объему, и так до тех пор, пока не будут отобраны те группы или отдельные единицы, которые необходимо исследовать.

Выборочный отбор может быть повторным и бесповторным. При повторном отборе вероятность выбора любой единицы не ограничена. При бесповторном отборе выбранная единица в исходную совокупность не возвращается.

Для отобранных единиц рассчитываются обобщенные показатели (средние или относительные) и в дальнейшем результаты выборочного исследования распространяются на всю генеральную совокупность.

Основной задачей при выборочном исследовании является определение ошибок выборки. Принято различать среднюю и предельную ошибки выборки. Для иллюстрации можно предложить расчет ошибки выборки на примере простого случайного отбора.

Расчет средней ошибки повторной простой случайной выборки производится следующим образом:

cредняя ошибка для средней

 (11.1)

cредняя ошибка для доли

 (11.2)

Расчет средней ошибки бесповторной случайной выборки:

средняя ошибка для средней

 (11.3)

средняя ошибка для доли

 (11.4)

Расчет предельной ошибки повторной случайной выборки:

предельная ошибка для средней

предельная ошибка для доли

 (11.5)

где t - коэффициент кратности;

Расчет предельной ошибки бесповторной случайной выборки:

предельная ошибка для средней

 (11.6)

предельная ошибка для доли

 (11.7)

Следует обратить внимание на то, что под знаком радикала в формулах при бесповторном отборе появляется множитель, где N - численность генеральной совокупности.

Все вышеприведенные формулы применимы для большой выборки. Кроме большой выборки используются так называемые малые выборки (n < 30), которые могут иметь место в случаях нецелесообразности использования больших выборок.

При расчете ошибок малой выборки необходимо учесть два момента:

1) формула средней ошибки имеет вид

 (11.11)

2) при определении доверительных интервалов исследуемого показателя в генеральной совокупности или при нахождении вероятности допуска той или иной ошибки необходимо использовать таблицы вероятности Стьюдента, где Р = S (t, n), при этом Р определяется в зависимости от объема выборки и t.

6. Ряды динамики. Основные показатели изменения уровней ряда. Средние показатели.

Изменение социально-экономических явлений во времени изучается статистикой методом построения и анализа динамических рядов. Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности.

Базисные показатели характеризуют итоговый результат всех изменений в уровнях ряда от периода базисного уровня до данного (i-го) периода.

Цепные показатели характеризуют интенсивность изменения уровня от одного периода к другому в пределах того промежутка времени, который исследуется.

Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.

Абсолютный прирост (базисный)

где y_i - уровень сравниваемого периода; y₀ - уровень базисного периода.

Абсолютный прирост с переменной базой (цепной), который называют скоростью роста,

где y_i - уровень сравниваемого периода; y_i-1 - уровень предшествующего периода.

Коэффициент роста K_i определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.

Коэффициент роста базисный

Коэффициент роста цепной

Темп роста

Темп прироста Т_П определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному.

Темп прироста базисный

Темп прироста цепной

Темп прироста можно рассчитать и иным путем: как разность между темпом роста и 100 % или как разность между коэффициентом роста и 1 (единицей):

1) Т_п = Т_р - 100%; 2) Т_п = K_i - 1.

Абсолютное значение одного процента прироста A_i . Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.

Данный показатель рассчитывают по формуле

Для характеристики динамики изучаемого явления за продолжительный период рассчитывают группу средних показателей динамики. Можно выделить две категории показателей в этой группе: а) средние уровни ряда; б) средние показатели изменения уровней ряда.

Средние уровни ряда рассчитываются в зависимости от вида временного ряда.

Для интервального ряда динамики абсолютных показателей средний уровень ряда рассчитывается по формуле простой средней арифметической:

где n - число уровней ряда.

Для моментного динамического ряда средний уровень определяется следующим образом.

Средний уровень моментного ряда с равными интервалами рассчитывается по формуле средней хронологической:

где n - число дат.

Средний уровень моментного ряда с неравными интервалами рассчитывается по формуле средней арифметической взвешенной, где в качестве весов берется продолжительность промежутков времени между временными моментами изменений в уровнях динамического ряда:

где t - продолжительность периода (дни, месяцы), в течение которого уровень не изменялся.

Средний абсолютный прирост (средняя скорость роста) определяется как средняя арифметическая из показателей скорости роста за отдельные периоды времени:

где y_n - конечный уровень ряда; y₁ - начальный уровень ряда.

Средний коэффициент роста () рассчитывается по формуле средней геометрической из показателей коэффициентов роста за отдельные периоды:

где К_р1 , К_р2 , ..., К_{р n-1} - коэффициенты роста по сравнению с предыдущим периодом; n - число уровней ряда.

Средний коэффициент роста можно определить иначе:

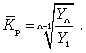
Средний темп роста, %. Это средний коэффициент роста, который выражается в процентах:

Средний темп прироста , %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу:

Среднее абсолютное значение 1% прироста можно рассчитать по формуле

6. Ряды динамики. Составляющие ряда динамики. Методы выявления основной тенденции (тренда). Измерение колеблемости ряда.

Изменение социально-экономических явлений во времени изучается статистикой методом построения и анализа динамических рядов. Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности.

Измените уровней ряда динамики обуславливается на изучаемое явление определяющее влияние и формируют в рядах динамики основную тенденцию развития (тренд) Воздействие факторов действующих периодически вызывает повторяемые во времени колебания уровней ряда динамики . Действие разовых факторов отображается случайными (кратковременных) изменениями уровней ряда дин-ки. Т.т ряд дин-ки вкл след основ. компоненты : 1)основ тенденция (тренд) 2)циклические (периодические колебания) 3)Случайные колебания Основной тенденцией развития (трендом) наз-ся плавное и устойчивое изменения уровня явлений во времени свободное от случ. Колебний. Выявление основ тенденции изменения уровней ряда предполагает её количественное выражение в некоторой мере свободное от случайных воздействий. Для выявления тренда испо-ся различные способы сглаживания (выравнивания ряда) : 1)Метод укрепления интервалов – заключ-ся в том что первоначальный ряд динамики преобразуется в ряд более продолжительных периодов (Напр. ряд, содержащий данные в месячном выпуске продукции преобразуется в ряд квартальных данных) 2)Метод скользящей средней. Состоит в том сто исходные уровни ряда заменяются средними величинами, к-рые получают из данного уровня и нескольких симметрично его окружающих. Число уровней, поск-ым рассчитываются сред. значение наз-ся интервалом сглаживания, он мож. четным и нечетным. Расчет средних ведется способом скольжения, т.е. постепенным исключением их принятого периода скольжения. 1-ого уровня и включением следующего. Нахождение скользящей средней по четному числу уровней осложняется тем, что средняя мож быть отнесена толь. к середине укрупненного интер-ла. Поэт. для определения сглаженных уровней производится центрирование, т.е. нахождение средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. 3)Аналитическое выравнивание. Суть метода заключается в подборе матем. Функции, к-рая наилучшим образом характеризует исходные уровни ряда динамики. Эмпирические (фактические) уровни ряда динамики заменяют на плавно изменяющиеся теоретические уровни, рассчитанные по какой-либо функц. Зависимости отклонение исходных уровней ряда от уровней, соответ-щих общей тенденции объясняется действием случайных или периодических факторов. Для выравнивания используют след. матем. Функции : а) линейная y_t=a₀+a₁ty₁ – значение выравненного ряда (теортетич-кие уровни) a₀,a₁ – параметры прямых t – показатель времени б)параболическая y_t = a₀ + a₁t + a₂t² в) гиперболическая yt = a₀ + a₁ * 1/t г) логарифмическая

y_t = a₀ + a₁ * lgt д) экспоненциальная y_t = a₀ * a₁^t Выбор ф-ции производится на основе анализа характера закономерностей дин-ки изучаемого явления. В практике стат. изучения тренда различ. След типы развития явлений во времени :

1)равномерное развитие, к-рому присущи постоянные приросты. Основная тенденция отображается уравнением прямой.

2)равноускоренное развитие. Уровни таких рядов динамики изменяются с постоянными темпами прироста. Основная тенденция отображается функцией параболы 2-ого порядка.

3)Развитие с переменным ускорением (замедление). Основная тенденция отображается функцией параболы 3-ого порядка.

4)развитие по экспоненте характеризует стабильные темпы роста.

6. Экономические индексы. Индивидуальные и агрегатные индексы.

Индексами называют сравнительные относительные величины, которые характеризуют изменение сложных социально-экономических показателей (показатели, состоящие из несуммируемых элементов) во времени, в пространстве, по сравнению с планом.

Индекс - это результат сравнения двух одноименных показателей, при исчислении которого следует различать числитель индексного отношения (сравниваемый или отчетный уровень) и знаменатель индексного отношения (базисный уровень, с которым производится сравнение). Выбор базы зависит от цели исследования. Если изучается динамика, то за базисную величину может быть взят размер показателя в периоде, предшествующем отчетному. Если необходимо осуществить территориальное сравнение, то за базу можно принять данные другой территории. За базу сравнения могут приниматься плановые показатели, если необходимо использовать индексы как показатели выполнения плана.

Индивидуальные индексы (i) - это индексы, которые характеризуют изменение только одного элемента совокупности.

Общий (сводный) индекс (I) характеризует изменение по всей совокупности элементов сложного явления. Если индексы охватывают только часть явления, то их называют групповыми. В зависимости от способа изучения общие индексы могут быть построены или как агрегатные (от лат. аggrega - присоединяю) индексы, или как средние взвешенные индексы (средние из индивидуальных).

Способ построения агрегатных индексов заключается в том, что при помощи так называемых соизмерителей можно выразить итоговые величины сложной совокупности в отчетном и базисном периодах, а затем первую сопоставить со второй.

В зависимости от характера и содержания индексируемых величин различают индексы количественных (объемных) показателей и индексы качественных показателей.

Индекс физического объема продукции (ФОП) отражает изменение выпуска продукции.

Индивидуальный индекс ФОП отражает изменение выпуска продукции одного вида и определяется по формуле

где q₁ и q₀ - количество продукции данного вида в натуральном выражении в текущем и базисном периодах.

Агрегатный индекс ФОП (предложен Э. Ласпейресом) отражает изменение выпуска всей совокупности продукции, где индексируемой величиной является количество продукции q, а соизмерителем - цена р:

где q₁ и q₀ - количество выработанных единиц отдельных видов продукции соответственно в отчетном и базисном периодах; p₀ - цена единицы продукции (отдельного вида) в базисном периоде.

При вычислении индекса ФОП в качестве соизмерителей может выступать также себестоимость продукции или трудоемкость.

Аналогично рассчитывается индекс затрат на выпуск продукции (ЗВП), который отражает изменение затрат на производство и может быть как индивидуальным, так и агрегатным.

Индивидуальный индекс ЗВП отражает изменение затрат на производство одного вида и определяется по формуле

где z₁ и z₀ - себестоимость единицы продукции искомого вида в текущем и базисном периодах; q₁ z₁ и q₀ z₀ - суммы затрат на выпуск продукции искомого вида в текущем и базисном периодах.

Агрегатный индекс ЗВП характеризует изменение общей суммы затрат на выпуск продукции за счет изменения количества выработанной продукции и ее себестоимости и определяется по формуле

где q₁ z₁ и q₀ z₀ - затраты на выпуск продукции каждого вида соответственно в отчетном и базисном периодах.

Рассмотрим построение индекса стоимости продукции (СП), который может определяться и как индивидуальный, и как агрегатный.

Индивидуальный индекс СП характеризует изменение стоимости продукции данного вида и имеет вид:

где p₁ и p₀ - цена единицы продукции данного вида в текущем и базисном периодах; q₁ p₁ и q₀ p₀ - стоимость продукции данного вида в текущем и базисном периодах.

Агрегатный индекс СП (товарооборота) характеризует изменение общей стоимости продукции за счет изменения количества продукции и цен и определяется по формуле

Качественные показатели определяют уровень исследуемого итогового показателя и определяются путем соотношения итогового показателя и определенного количественного показателя (например, средняя заработная плата определяется путем соотношения фонда заработной платы и количества работников). К индексам качественных показателей относятся индексы цен, себестоимости, средней заработной платы, производительности труда.

Самым распространенным индексом в этой группе является индекс цен.

Индивидуальный индекс цен характеризует изменение цен по одному виду продукции и определяется по формуле

где p₁ и p₀ - цена за единицу продукции в текущем и базисном периодах.

Соответственно определяются индексы себестоимости и затрат рабочего времени по каждому виду продукции.

Агрегатный индекс цен определяет среднее изменение цены р по совокупности определенных видов продукции q.

Для характеристики среднего изменения цен на потребитель-ские товары используют индекс цен, предложенный Э. Ласпейресом (индекс Ласпейреса):

где q₀ - потребительская корзина (базовый период); p₀ и p₁ - соответственно цены базисного и отчетного периодов.

Если количество набора продуктов принимается на уровне отчетного периода (q₁ ), то в этом случае индекс цен именуется индексом Пааше:

В статистической практике очень широко используется агрегатный территориальный индекс цен, который может быть рассчитан по следующей формуле:

где p_A p_B - цена за единицу продукции каждого вида соответственно на территории А и В; q_A - количество выработанной или реализованной продукции каждого вида по территории А (в натуральном выражении).

Из формулы видно, что в данном индексе в качестве фиксированного показателя (веса) принят объем продукции территории А. При расчете данного индекса в качестве веса можно принять также объем продукции территории В или суммарный объем продукции двух территорий.

Возможны два способа расчета индексов: цепной и базисный.

Цепные индексы получают путем сопоставления текущих уровней с предшествующим, при этом база сравнения постоянно меняется.

Базисные индексы получают путем сопоставления с тем уровнем периода, который был принят за базу сравнения.

В качестве примера можно привести цепные и базисные индексы цен.

Цепные индивидуальные индексы цен имеют следующий ряд расчета:

Базисные индивидуальные индексы цен:

Следует помнить, что произведение цепных индивидуальных индексов цен равно последнему базисному индексу:

Цепные агрегатные индексы цен:

Базисные агрегатные индексы цен:

Между индексами существует также взаимосвязь и взаимозависимость, как и между самими экономическими явлениями, что позволяет проводить факторный анализ. Благодаря индексному методу можно рассматривать все факторы независимо друг от друга, что дает возможность определить размер абсолютного изменения сложного явления за счет каждого фактора в отдельности.

Предположим, что результативный признак зависит от трех факторов и более. В этом случае результативный индекс примет вид

Изменение результативного индекса за счет каждого фактора может быть выражено следующим образом:

Для выявления роли каждого фактора в отдельности индекс сложного показателя разлагают на частные (факторные) индексы, которые характеризуют роль каждого фактора. При этом используют два метода:

• метод обособленного изучения факторов;

• последовательно-цепной метод.

При первом методе сложный показатель берется с учетом изменения лишь того фактора, который взят в качестве исследуемого, все остальные остаются неизменными на уровне базисного периода.

Последовательно-цепной метод предполагает использование системы взаимосвязанных индексов, которая требует определенного расположения факторов. Как правило, на первом месте в цепи располагают качественный фактор. При определении влияния первого фактора все остальные сохраняются в числителе и знаменателе на уровне базисного периода, при определении второго факторного индекса первый фактор сохраняется на уровне базисного периода, а третий и все последующие - на уровне отчетного периода, при определении третьего факторного индекса первый и второй факторы сохраняются на уровне базисного периода, четвертый и все остальные - на уровне отчетного периода и т.д.

6. Экономические индексы. Индивидуальные индексы и средние индексы из индивидуальных. Индексы переменного и фиксированного составов. Индекс структурных сдвигов.

Индексами называют сравнительные относительные величины, которые характеризуют изменение сложных социально-экономических показателей (показатели, состоящие из несуммируемых элементов) во времени, в пространстве, по сравнению с планом.

Индекс - это результат сравнения двух одноименных показателей, при исчислении которого следует различать числитель индексного отношения (сравниваемый или отчетный уровень) и знаменатель индексного отношения (базисный уровень, с которым производится сравнение). Выбор базы зависит от цели исследования. Если изучается динамика, то за базисную величину может быть взят размер показателя в периоде, предшествующем отчетному. Если необходимо осуществить территориальное сравнение, то за базу можно принять данные другой территории. За базу сравнения могут приниматься плановые показатели, если необходимо использовать индексы как показатели выполнения плана.

Индексом переменного состава называют отношение двух средних уровней.

Индекс фиксированного состава есть средний из индивидуальных индексов. Он рассчитывается как отношение двух стандартизованных средних, где влияние изменения структурного фактора устранено, поэтому данный индекс называют еще индексом постоянного состава.

Средние взвешенные индексы ФОП используются в том случае, если известны индивидуальные индексы объема по отдельным видам продукции и стоимость отдельных видов продукции (или затраты) в базисном или отчетном периоде.

Средний взвешенный арифметический индекс ФОП определяется по формуле

где i_q - индивидуальный индекс по каждому виду продукции; q₀ p₀ - стоимость продукции каждого вида в базисном периоде.

Средний взвешенный гармонический индекс ФОП

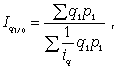
где q₁ p₁ - стоимость продукции каждого вида в текущем периоде.

Если известны индивидуальные индексы цен по отдельным видам продукции и стоимость отдельных видов продукции, то применяются средние взвешенные индексы цен (средний взвешенный арифметический и средний взвешенный гармонический индексы цен).

Формула среднего взвешенного арифметического индекса цен

где i - индивидуальный индекс по каждому виду продукции; p₀ q₀ - стоимость продукции каждого вида в базисном периоде.

Формула среднего взвешенного гармонического индекса цен

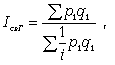
где p₁ q₁ - стоимость продукции каждого вида в текущем периоде.