15. Метод наименьших квадратов.

Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Примеры

Пример кривой, проведённой через точки, имеющие нормально распределённое отклонение от истинного значения. Пусть надо решить систему уравнений

(1)

число которых более числа неизвестных x, y,

Чтобы решить их по способу наименьших квадратов, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые, или так называемые нормальные уравнения составляются по следующему правилу: умножают сперва все данные уравнения на коэффициенты у первой неизвестной x и, сложив почленно, получают первое нормальное уравнение, умножают все данные уравнения на коэффициенты у второй неизвестной y и, сложив почленно, получают второе нормальное уравнение и т. д. Если обозначить для краткости:

то нормальные уравнения представятся в следующем простом виде:

(2)

Легко заметить, что коэффициенты нормальных уравнений весьма легко составляются из коэффициентов данных, и притом коэффициент у первой неизвестной во втором уравнении равен коэффициенту у второй неизвестной в первом, коэффициент у первой неизвестной в третьем уравнении равен коэффициенту у третьей неизвестной в первом и т. д

16. Регрессионный анализ. Теоретическое корреляционное отношение и линейный коэффициент корреляции.

1. Определение регрессии. Регрессия — функция, позволяющая по средней величине одного признака определить среднюю величину другого признака, корреляционно связанного с первым.

С этой целью применяется коэффициент регрессии и целый ряд других параметров. Например, можно рассчитать число простудных заболеваний в среднем при определенных значениях среднемесячной температуры воздуха в осенне-зимний период.

2. Определение коэффициента регрессии. Коэффициент регрессии — абсолютная величина, на которую в среднем изменяется величина одного признака при изменении другого связанного с ним признака на установленную единицу измерения.

3. Формула коэффициента регрессии. R_у/х = r_ху x (σ_у / σ_x)  где R_у/х — коэффициент регрессии;  r_ху — коэффициент корреляции между признаками х и у;  (σ_у и σ_x) — среднеквадратические отклонения признаков x и у.

В нашем примере [r_ху = - 0,96 коэффициент корреляции между изменениями среднемесячной температуры в осенне-зимний период (х) и средним числом инфекционно-простудных заболеваний (у)];  σ_х = 4,6 (среднеквадратическое отклонение температуры воздуха в осенне-зимний период;  σ_у = 8,65 (среднеквадратическое отклонение числа инфекционно-простудных заболеваний).  Таким образом, R_у/х — коэффициент регрессии.  R_у/х = -0,96 х (4,6 / 8,65) = 1,8, т.е. при снижении среднемесячной температуры воздуха (x) на 1 градус среднее число инфекционно-простудных заболеваний (у) в осенне-зимний период будет изменяться на 1,8 случаев.

4. Уравнение регрессии. у = М_у + R_y/x (х - М_x)  где у — средняя величина признака, которую следует определять при изменении средней величины другого признака (х);  х — известная средняя величина другого признака;  R_y/x — коэффициент регрессии;  М_х, М_у — известные средние величины признаков x и у.

Например, среднее число инфекционно-простудных заболеваний (у) можно определить без специальных измерений при любом среднем значении среднемесячной температуры воздуха (х). Так, если х = - 9°, R_у/х = 1,8 заболеваний, М_х = -7°, М_у = 20 заболеваний, то у = 20 + 1,8 х (9-7) = 20 + 3,6 = 23,6 заболеваний.  Данное уравнение применяется в случае прямолинейной связи между двумя признаками (х и у).

5. Назначение уравнения регрессии. Уравнение регрессии используется для построения линии регрессии. Последняя позволяет без специальных измерений определить любую среднюю величину (у) одного признака, если меняется величина (х) другого признака. По этим данным строится график — линия регрессии, по которой можно определить среднее число простудных заболеваний при любом значении среднемесячной температуры в пределах между расчетными значениями числа простудных заболеваний.

6. Сигма регрессии (формула).

где σ_Rу/х — сигма (среднеквадратическое отклонение) регрессии;  σ_у— среднеквадратическое отклонение признака у;  r_ху — коэффициент корреляции между признаками х и у.

Так, если σ_у - среднеквадратическое отклонение числа простудных заболеваний = 8,65; r_ху — коэффициент корреляции между числом простудных заболеваний (у) и среднемесячной температурой воздуха в осенне-зимний период (х) равен — 0,96, то

7. Назначение сигмы регрессии. Дает характеристику меры разнообразия результативного признака (у).

Например, характеризует разнообразие числа простудных заболеваний при определенном значении среднемесячной температуры воздуха в осеннне-зимний период. Так, среднее число простудных заболеваний при температуре воздуха х₁ = -6° может колебаться в пределах от 15,78 заболеваний до 20,62 заболеваний.  При х₂ = -9° среднее число простудных заболеваний может колебаться в пределах от 21,18 заболеваний до 26,02 заболеваний и т.д.

Сигма регрессии используется при построении шкалы регрессии, которая отражает отклонение величин результативного признака от среднего его значения, отложенного на линии регрессии.

8. Данные, необходимые для расчета и графического изображения шкалы регрессии

• коэффициент регрессии — R_у/х;

• уравнение регрессии — у = М_у + R_у/х (х-М_x);

• сигма регрессии — σ_Rx/y

Другая важнейшая задача - измерение тесноты зависимости - для всех форм связи может быть решена при помощи вычисления эмпирического корреляционного отношения :

где - дисперсия в ряду выравненных значений результативного показателя;- дисперсия в ряду фактических значений у.

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать, например, две следующие формулы:

Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.

16. Регрессионный анализ. Ошибки оценок коэффициентов регрессии. Проверка гипотез о значимости коэффициентов регрессии и уравнения регрессии в целом.

Определение регрессии. Регрессия — функция, позволяющая по средней величине одного признака определить среднюю величину другого признака, корреляционно связанного с первым.

С этой целью применяется коэффициент регрессии и целый ряд других параметров. Например, можно рассчитать число простудных заболеваний в среднем при определенных значениях среднемесячной температуры воздуха в осенне-зимний период.

Определение коэффициента регрессии. Коэффициент регрессии — абсолютная величина, на которую в среднем изменяется величина одного признака при изменении другого связанного с ним признака на установленную единицу измерения.

Формула коэффициента регрессии. R_у/х = r_ху x (σ_у / σ_x)  где R_у/х — коэффициент регрессии;  r_ху — коэффициент корреляции между признаками х и у;  (σ_у и σ_x) — среднеквадратические отклонения признаков x и у.

В нашем примере [r_ху = - 0,96 коэффициент корреляции между изменениями среднемесячной температуры в осенне-зимний период (х) и средним числом инфекционно-простудных заболеваний (у)];  σ_х = 4,6 (среднеквадратическое отклонение температуры воздуха в осенне-зимний период;  σ_у = 8,65 (среднеквадратическое отклонение числа инфекционно-простудных заболеваний).  Таким образом, R_у/х — коэффициент регрессии.  R_у/х = -0,96 х (4,6 / 8,65) = 1,8, т.е. при снижении среднемесячной температуры воздуха (x) на 1 градус среднее число инфекционно-простудных заболеваний (у) в осенне-зимний период будет изменяться на 1,8 случаев.

Уравнение регрессии. у = М_у + R_y/x (х - М_x)  где у — средняя величина признака, которую следует определять при изменении средней величины другого признака (х);  х — известная средняя величина другого признака;  R_y/x — коэффициент регрессии;  М_х, М_у — известные средние величины признаков x и у.

Например, среднее число инфекционно-простудных заболеваний (у) можно определить без специальных измерений при любом среднем значении среднемесячной температуры воздуха (х). Так, если х = - 9°, R_у/х = 1,8 заболеваний, М_х = -7°, М_у = 20 заболеваний, то у = 20 + 1,8 х (9-7) = 20 + 3,6 = 23,6 заболеваний.  Данное уравнение применяется в случае прямолинейной связи между двумя признаками (х и у).

Назначение уравнения регрессии. Уравнение регрессии используется для построения линии регрессии. Последняя позволяет без специальных измерений определить любую среднюю величину (у) одного признака, если меняется величина (х) другого признака. По этим данным строится график — линия регрессии, по которой можно определить среднее число простудных заболеваний при любом значении среднемесячной температуры в пределах между расчетными значениями числа простудных заболеваний.

Сигма регрессии (формула).

где σ_Rу/х — сигма (среднеквадратическое отклонение) регрессии;  σ_у— среднеквадратическое отклонение признака у;  r_ху — коэффициент корреляции между признаками х и у.

Так, если σ_у - среднеквадратическое отклонение числа простудных заболеваний = 8,65; r_ху — коэффициент корреляции между числом простудных заболеваний (у) и среднемесячной температурой воздуха в осенне-зимний период (х) равен — 0,96, то

Назначение сигмы регрессии. Дает характеристику меры разнообразия результативного признака (у).

Например, характеризует разнообразие числа простудных заболеваний при определенном значении среднемесячной температуры воздуха в осеннне-зимний период. Так, среднее число простудных заболеваний при температуре воздуха х₁ = -6° может колебаться в пределах от 15,78 заболеваний до 20,62 заболеваний.  При х₂ = -9° среднее число простудных заболеваний может колебаться в пределах от 21,18 заболеваний до 26,02 заболеваний и т.д.

Сигма регрессии используется при построении шкалы регрессии, которая отражает отклонение величин результативного признака от среднего его значения, отложенного на линии регрессии.

Данные, необходимые для расчета и графического изображения шкалы регрессии

1. коэффициент регрессии — R_у/х;

2. уравнение регрессии — у = М_у + R_у/х (х-М_x);

3. сигма регрессии — σ_Rx/y

Стандартная ошибка является оценкой среднего квадратичного отклонения коэффициента регрессии от его истинного значения. Позволяет получить некоторое представление о форме функции плотности вероятности, однако не несёт информации о том, находится ли полученная оценка в середине распределения (т.е. является точной) или в его «хвосте» (т.е. является относительно неточной).

проверке гипотезы H0 остатистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт  и критического (табличного) Fтабл значений F-критерия Фишера. Fфактопределяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где   n – число единиц совокупности;

        m – число параметров при переменных x.

Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a  –  вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.

Если  Fтабл< Fфакт, то H0  – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если  Fтабл> Fфакт, то H0 – гипотеза не отклоняется и признается статистическая незначимость, надежность уравнения регрессии.

2.  t-критерий Стьюдента используется для оценки статистической значимости коэффициентов регрессии и коэффициента  корреляции.

В качестве основной гипотезы вы­двигают гипотезу H0 о незначимом отличии от нуля параметра регрессии или коэффициента корреляции. Альтернативной гипотезой, при этом является гипотеза обратная, т.е. о неравенстве нулю параметра или коэффициента корреляции.

Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактиче­ским) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (ко­торые обычно приводятся в конце учебников и практикумов по статистике или эконометрике).

Табличное значение оп­ределяется в зависимости от уровня значимости (a) и числа степеней свободы, которое в случае линейной парной рег­рессии равно (n-2) , n - число наблюдений.

Если фактическое значение t-критерия больше таб­личного (по модулю), то считают, что с вероятностью (1-a) параметр регрессии (ко­эффициент корреляции) значимо отличается от нуля.

Если фактическое значение t-критерия меньше таб­личного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр регрессии (коэффициент корреля­ции) незначимо отличается от нуля при уровне значимости a.

Фактические значения t-критерия определяются по формулам:

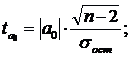
где   

Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции используют критерий:

где r - оценка коэффициента корреляции, полученная по наблюдаемым данным. tтабл  остается прежним.

 

3.  Адекватность регрессионной модели оценим с помощью средней ошибки аппроксимации – среднее отклонение расчетных значений от фактических:

Допустимый предел значений  –  не более 8-10%.

16. Линейный коэффициент корреляции и коэффициент Фехнера. Проверка линейного коэффициента корреляции на значимость.

Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать, например, две следующие формулы:

Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.

коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле

где n_a - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической; n_b - соответственно количество несовпадений.

Коэффициент Фехнера может изменяться в пределах -1,0 К_ф  +1,0.

проверке гипотезы H0 остатистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт  и критического (табличного) Fтабл значений F-критерия Фишера. Fфактопределяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

где   n – число единиц совокупности;

        m – число параметров при переменных x.

Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a  –  вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.

Если  Fтабл< Fфакт, то H0  – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если  Fтабл> Fфакт, то H0 – гипотеза не отклоняется и признается статистическая незначимость, надежность уравнения регрессии.

2.  t-критерий Стьюдента используется для оценки статистической значимости коэффициентов регрессии и коэффициента  корреляции.

В качестве основной гипотезы вы­двигают гипотезу H0 о незначимом отличии от нуля параметра регрессии или коэффициента корреляции. Альтернативной гипотезой, при этом является гипотеза обратная, т.е. о неравенстве нулю параметра или коэффициента корреляции.

Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактиче­ским) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (ко­торые обычно приводятся в конце учебников и практикумов по статистике или эконометрике).

Табличное значение оп­ределяется в зависимости от уровня значимости (a) и числа степеней свободы, которое в случае линейной парной рег­рессии равно (n-2) , n - число наблюдений.

Если фактическое значение t-критерия больше таб­личного (по модулю), то считают, что с вероятностью (1-a) параметр регрессии (ко­эффициент корреляции) значимо отличается от нуля.

Если фактическое значение t-критерия меньше таб­личного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр регрессии (коэффициент корреля­ции) незначимо отличается от нуля при уровне значимости a.

Фактические значения t-критерия определяются по формулам:

где   

Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции используют критерий:

где r - оценка коэффициента корреляции, полученная по наблюдаемым данным. tтабл  остается прежним.

 

3.  Адекватность регрессионной модели оценим с помощью средней ошибки аппроксимации – среднее отклонение расчетных значений от фактических:

Допустимый предел значений  –  не более 8-10%.

19. Коэффициенты корреляции рангов.

В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые непараметрические методы.

Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируются не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом.

Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены . Спирмэном и М. Кендэлом.

Коэффициент корреляции рангов Спирмэна (р) основан на рассмотрении разности рангов значений результативного и факторного признаков и может быть рассчитан по формуле

где d = N_x - N_y , т.е. разность рангов каждой пары значений х и у; n - число наблюдений.

Ранговый коэффициент корреляции Кендэла () можно определить по формуле

где S = P + Q.

К непараметрическим методам исследования можно отнести коэффициент ассоциации К_ас и коэффициент контингенции К_кон , которые используются, если, например, необходимо исследовать тесноту зависимости между качественными признаками, каждый из которых представлен в виде альтернативных признаков.

Для определения этих коэффициентов создается расчетная таблица (таблица «четырех полей»), где статистическое сказуемое схематически представлено в следующем виде:

Признаки	А (да)	А (нет)	Итого
В (да)	a	b	a + b
В (нет)	с	d	c + d
Итого	a + c	b + d	n

Здесь а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков ; n - общая сумма частот.

Коэффициент ассоциации можно расcчитать по формуле

Коэффициент контингенции рассчитывается по формуле

Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации.

19. Показатели тесноты связи между двумя качественными признаками. Проверка гипотезы о существенности связи.

Коэффициент ассоциации К_ас и коэффициент контингенции К_кон , которые используются, если, например, необходимо исследовать тесноту зависимости между качественными признаками, каждый из которых представлен в виде альтернативных признаков. Для определения этих коэффициентов создается расчетная таблица (таблица «четырех полей»), где статистическое сказуемое схематически представлено в следующем виде:

Признаки	А (да)	А (нет)	Итого
В (да)	a	b	a + b
В (нет)	с	d	c + d
Итого	a + c	b + d	n

Здесь а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков ; n - общая сумма частот.

Коэффициент ассоциации можно расcчитать по формуле 

Коэффициент контингенции рассчитывается по формуле