
Производящие и характеристические функции.
Характеристической функцией случайной величины называется функция действительного переменного t
f(t)=Eeit, –<t<+,
в частности, если распределение абсолютно непрерывно и имеет плотность (x), то
![]() ,
,
если –дискретная случайная величина, то
![]() .
.
Производящей функцией случайной величины называется функция комплексного переменного z
![]() ,
|z|1.
,
|z|1.
Свойства характеристической функции:
1. Если P{||<}=1, то f(0)=(1)=1.
2.
Если E
||k<
для некоторого целого k1,
то
![]() ,
,![]() .
.
3. Если случайные величины 1,…, n независимы, то
![]() ,
,
![]() .
.
В
частности,
![]() ,
,![]() .
.
Закон больших чисел. Центральная предельная теорема.
Пусть 1,2,…n–независимые одинаково распределенные случайные величины, причемEj=a, Dj==2<. Тогда
![]() для любого>0,
(1)
для любого>0,
(1)
Соотношение (1) называется законом больших чисел.
Центральная предельная теорема. Если 1,2,…–независимые одинаково распределенные случайные величины, En=a, Dn=2< (n=1,2,…),то для любых–<x1< x2<,
 .
.
Цепи Маркова. Определение. Марковское свойство.
Цепь Маркова является моделью зависимых испытаний, в которых исход в данном испытание зависит лишь от последнего известного исхода и не зависит от более далекого прошлого. Обычно исходы в цепях Маркова называются состояниями цепи Маркова.
Будем считать, что nсостояний цепи Маркова занумерованы
числами 1, 2,…,n.
Элементарным событием вmиспытаниях цепи Маркова является цепочки
состояний, или исходов, длиныm+1,
описывающие начальное состояние и
результатыmиспытаний:
(i0, i1,…,
im). Здесь
исходitможет при любомt(t=![]() )
может принимать любое значение 1, 2,…,n.
Таким образом, множество элементарных
событий
)
может принимать любое значение 1, 2,…,n.
Таким образом, множество элементарных
событий
m={
(i0, i1,…,
im):it=![]() ,t=
,t=![]() }.
}.
Если обозначить Atисход в испытанииtцепи Маркова, то условие независимости от более далекого прошлого можно записать в виде
P(At+1|
A0…At)=
P(At+1|
At),
t= ![]() .
(1)
.
(1)
Иногда номер испытания называют моментом времени.
Мы будем предполагать, что цепь Маркова
однородна во времени. Пусть событием
Atявляется наступление исходаiвt-м испытании, аAt+1является наступление исходаjв (t+1)-м испытании.
В этом случаеP(At+1|At)=pij,t=![]() .
Вероятностьpijявляется условной вероятностью того,
что в испытанииt+1
состоянием цепи Маркова былоj,
если в моментtсостояниемi. Эти
вероятности называютсявероятностями
перехода или переходными вероятностями.
.
Вероятностьpijявляется условной вероятностью того,
что в испытанииt+1
состоянием цепи Маркова былоj,
если в моментtсостояниемi. Эти
вероятности называютсявероятностями
перехода или переходными вероятностями.
Если задать вероятности q0,…,
qnначальных состояний (состояний перед
началом испытаний) цепи Маркова и
переходные вероятностиpij(i,j=![]() ),
то
),
то
P(i0,
i1,…, im)=![]() .
.
Для задания вероятностей достаточно задать матрицу вероятностей перехода
 ,pij0,
,pij0,![]() ,
(i,j=
,
(i,j=![]() )
)
и вектор
начальных состояний(q0,…,
qn),qj0,j=![]() ,
,![]() .
.
Цепи Маркова 2
Пусть t (t=0, 1, 2,…) состояние однородной цепи Маркова в моментt. Положимpij(t)=P{t=j|0=i}. Тогда (системы уравнений Колмогорова)
![]() .
.
Обозначим P(t) матрицу вероятностей переходаpij(t):
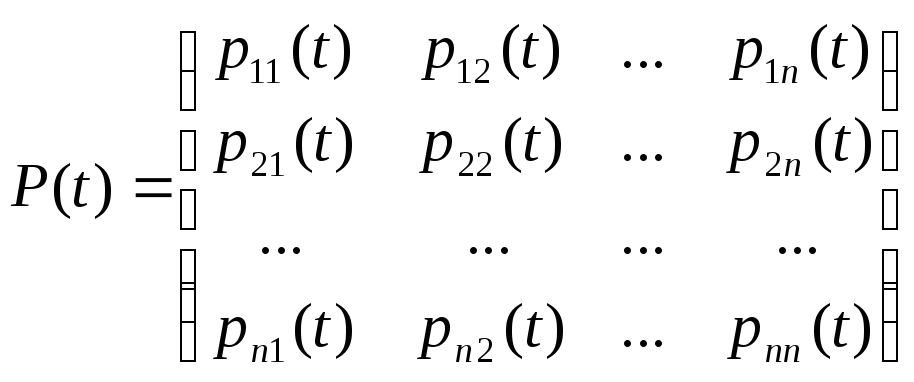 .
.
Тогда P(t+s)=P(t)P(s),P(t)=Pt, гдеP=P(1) – матрица вероятностей перехода за один шаг.
Теорема.Если при некотором t0>0
все элементы матрицы
![]() положительны,
то существуют положительные пределы
положительны,
то существуют положительные пределы
![]()
и не зависят от начального состояния. Предельные вероятности удовлетворяют системе уравнений
![]()
Распределение 1,…,nназываетсястационарным распределением.
Обозначим j(t) время пребывания, или число попаданий в состояниеj, цепи Маркова за времяt. Будем говорить, что частотаj(t)/tпопадания в состояниеjудовлетворяет закону больших чисел, если для любого>0 приt
![]() .
.
При изучении величины j(t) часто оказывается полезным ее представление в виде суммы:
j(t)= j(1)+ j(2)+…+ j(t),
где
j(s)=1,
если в моментs(s=![]() )
состоянием цепи былоj,
и j(s)=0
в противном случае.
)
состоянием цепи былоj,
и j(s)=0
в противном случае.
