Лекция №2

{Если нелинейная целевая функция и нелин. }

Дальнейшая классификация будет производиться последовательно.

Задача нелинейного программирования.

Условие существования экстремума целевой функции

(задача безусловной оптимизации)

Формулировка задачи:

–n-мерное Евклид. пространство

Все точки допустимы.

I

1. Обоснование необходимости изучения темы.

   1. Задача проще, лучше начинать с нее.

   2. Такие задачи редко, но на практике.

   3. переход от задачи условной оптимизации к безусловной.

2. Зачем нужны условия экстремума.

   1. Для оценки задачи (или нетmin)

   2. Нужны критерии как для построения методов решения задач, так и для остановки процесса поиска.

Основное внимание на теоремы, док-ва которых имеют конструктивный характер.

II. Определение min целевой функции

Определение: Скалярная функция n переменных :, т.е. вектор в скаляр наз-ся нормой вектора, если она удовлетворяет следующим трем условиям:

Нормированное пространство.

В рамках данного определения переход от вектора к скаляру определяется не единственным образом.

Евклидова норма вектора

;

Определение.

Т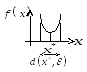.х наз. точка локации min ф-ии, если справедливо следующее:

Если в определении поменять знак на противоположный, то это будет определение лок. max.

Т. min и max называются экстремальными точками.

Для использования в алгоритмах это определение не годится по очевидным причинам. Поэтому такое определение будет использоваться только в теоретических выкладках.

Определение.Функция наз-ся унимодальной, если она в области определения имеет единственный min.

Если много экстремумов, то мультимодальной.

Min наз-ся глобальным, если внем ф-ия принимает наименьшее значение.

В унимодальной ф-ии локальные и глобальные min совпадают.

Поиску глобального min будет посвящена отдельная тема.

III.  экстремума.

Теорема Вейерштрасса.

Если ф-ия непрерывна и ограничена на , то она там имеет глобальныйmin.

Результат имеет слишком общий характер, практически ничего не дает для построения методов.

1) Условие  экстремума гладкой функции одной переменной.

Потребуем, чтобы функция была гладкой, чем выше порядок гладкости, тем лучше.

Гладкая в некоторой окрестности, если есть производная в этой окрестности.

Если первый порядок гладкости.

Мы считаем, что - т.min в необход. Все зависит от .

Пусть ф-ия имеет 2-й порядок гладкости.

Необходимое условие 1-го пор. формул в виде след. теоремы (Th. Ферма):

Пусть т.min и ф-ия диф. в этой точке ( хотя бы 1-я производная), тогда 1-я производная в т. min =0.

Док-во Th:

Получено противоречие, заключающееся в том, что в окрестности т.  т. с меньшим значением ф-ии, чем в т. min. Это противоречие устраняется, если производная равна 0.

Теорема доказана.

Обратим внимание на конструктивный характер доказательства Th.

Вдок-ве показан способ перехода из текущей точки в точку с меньшим значением ф-ии.

Производная в т., не равна 0.

, р надо выбирать очень маленьким.

Это лежит в основе построения градиентных методов оптимизации.

Основные задачи при нахождении min:

1. Выбрать направление.

2. Выбрать шаг.

Необходимое условие 2-го порядка:

Пусть т.min и в этой т. ф-ия 2 раза диф., тогда 2-я произв. ф-ии неотрицательна.

Определение. Т. наз-ся стационарной, если произв. ф-ии в этой точке равна 0.

Задача док-ть (на след. лекции)

Теорема достаточное условие экстремума.

Пусть стационарная точка и 2-я производная положительна в т., тогдат. лок.min.

Док-во:

Геометрическая иллюстрация этих теорем.