Метод замены переменных

Из системы уравнений необходимо определить:

Пример:

Характеристики метода:

1. Для использования этого метода нужна аналитическая зависимость от х услов. функции и огранич. (скорее всего будет алгоритм. зав.)

2. если будет такое ограничение, то нельзя разделить на зависимые и независимые переменные.

3. Даже если можно разделить на зависимые и независимые переменные, то нужна квалификация для решения системы.

Вывод: для практики такой подход не применим, а только для решения учебных задач.

Метод множителей Лагранжа

Позволяет:

1. Сформулировать необходимые условия  экстремума целевой функции при ограничениях типа равенств.

2. Свести задачу услов. оптим. к задаче безуслов. оптимизации.

Ф-я Лагранжа зависит от переменных.

Пусть при некотором найдено значение целевой ф-ии длятакое, что ф-я Лагранжа принимаетmin значение.

=0

Если т.  обл. огранич., видим, что min ф-ии Лагранжа будет совпадать с min ф-ии .

• Аналитический метод решения задачи (для оптимальных методов оптимизации)

• Численный (для решения практических задач)

Аналитический метод

- буквы

1. Найти

2. Подставить найденное значение в ограничения и найти числовое значение для всех 

3. Подставить найденные в и найти числовые значения.

Пример:

Теоретически можно построить численный метод:

построить ф-ию Лагранжа. используя  методы (Ньютона), найти все стационарные точки. Провести исследование всех стационарных точек, в том числе и седловых (седло может быть разделено по перем.  и х, из всех min по х выбрать наименьший.

Теорема (необходимое условие экстремума)

1. Пусть

2. 

Матрица якобы не вырождена.

Для того чтобы была т.min, необходимо, чтобы было решением следующей системы уравнений:

Лекция №5

Док-во:

Считаем, что - т.min должны получить .

В производной огранич. исп. правило дифференцирования сложной функции.

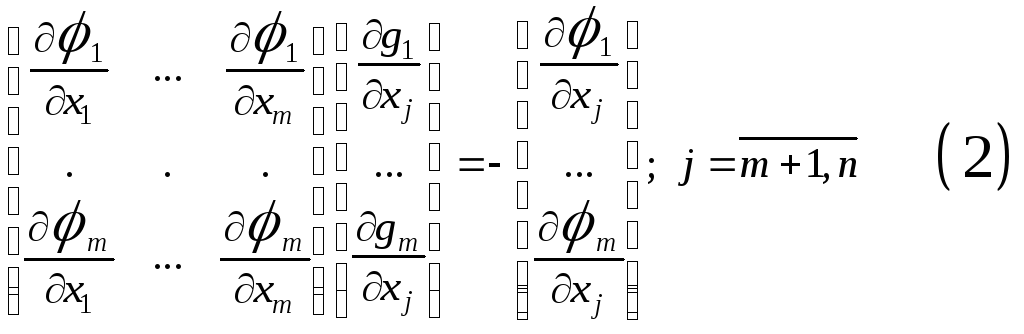
A

Если матрица не вырожд., то имеет одно решение.

Из  что могут быть определены однозначно.

3. Суммируем все ограничения при этом i-е ограничение умножаем на .

Изменим порядок суммирования в последнем выражении. Вынесем эл-ты типа

Прибавим к последнему выражению необх. условие экстремума из формулы .

Подставим , определяемые из системы .

= 0

Утверждение доказано (Th.)

Интерпретация множителей Лагранжа

Выводы по теме:

1. Отмечены 2 подхода к решению задач (зам. пер. и мн-ли Лагранжа).

2. Получены необх. условия экстремума для зад. услов. min с огран. типа равенства.

3. Приведена интерпрет. мн-й Лагранжа.

Лекция №6

Минимизация однопараметрической унимодальной функции

1. Формулировка задачи

Обоснование необходимости изучения темы.

1. 

а) такие задачи имеют место;

б) минимиз. многопараметр. ф-и сводится к решению последовательности задач минимиз. однопарам. ф-и.

Лекция №7

Особенности этой задачи:

1) Высокая вероятность того, что унимодальна.

2. Высокая трудоемкость, а иногда и не возможность вычисления производной:

а) может быть не диф.

б) если диф., то трудоемкость вычисл. производной очень высока (диф. по всем парам.)

Вывод: эта задача очень часто решается на практике. Надо изучать специфические методы (без использования производных) отыскания min.

Постановка задачи

Необходимо за конечное число шагов m или с точностью, локализовать т.min.

Можно установить связь между .

Основа рассматриваемого метода

Предполагая, что функция унимодальна, можно отбросить одну из частей (заведомо не содержащую т. min).

Общая характеристика метода

Методы делятся на 2 группы:

1. пассивная стратегия поиска min.

2. последовательная стратегия поиска:

выбираются порциями в процессе min ф-и. Выбор зависит от результата min на предыдущем шаге. Основная опер. выбор и вычисление. Облад. лучшей гибкостью и дают лучшие результаты.

Общее для 2-ой группы методов:

Отличие: в правилах генерации точек, трудоемкостью вычисления .

Можно классифицировать по исп. :

1 группа: нужны качественные оценки .

- узел интерполяции

Метод последовательного дихотомического поиска

На каждом шаге генерируются две точки, и в этих точках вычисляется значение функций. Наиболее трудоемкая операция – вычисление значения ф-й.

Точки генерируются по специальному правилу:

 - малое число, сравнимое с компьютерной погрешностью, генерируются близко к середине.

Если считать, что функция на каждом шаге вычисляется два раза, то

Если целевая функция вычисляется очень быстро, то можно применять этот метод.

Алгоритм:

Основная цель: обеспечить наиболее быстрое убывание отрезка неопредел. при min количестве вычислений целевой функции. Для достижения этой цели предлагается: на 1-ом шаге вычислить 2 значения целевой функции, на всех остальных – только 1 раз. Эта идея реализуется в методе Фибоначчи и в методе золотого сечения.