
щпоры по вм1 на первый семестр
.doc-
-
Предел функции в точке. Единственность предела. Ограниченность функции, имеющей предел. Связь функции, имеющей предел, и бесконечно малой функции.
Число А называется пределом функции f в точке а, если она определена на некоторой окрестности а, т.е. на некотором интервале (c,d), где c<a<d, за исключением, быть может, самой точки а, и если для всякого >0 можно указать зависящее от него >0 такое, что для всех x, для которых
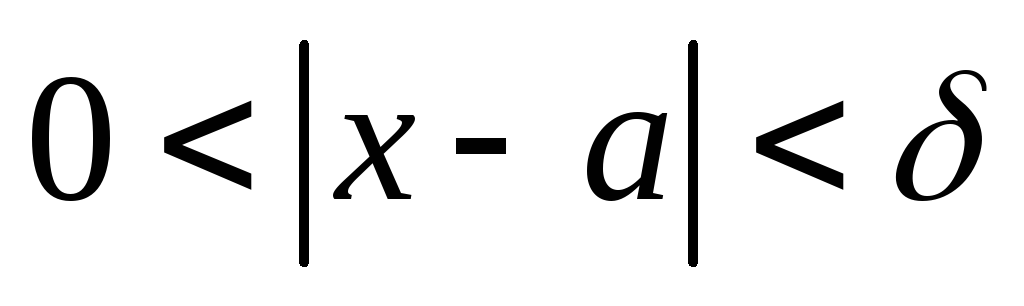 имеет место неравенство
имеет место неравенство
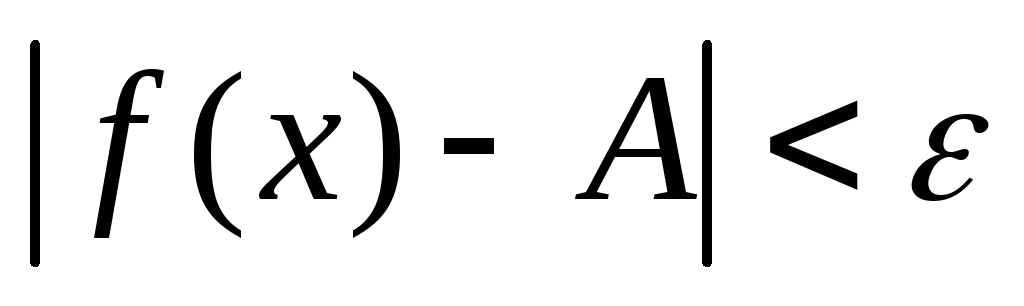 .
Тот факт, что А
есть предел f
в точке
a,
принято записывать
.
Тот факт, что А
есть предел f
в точке
a,
принято записывать
 или
или

 .
.Теорема. Если
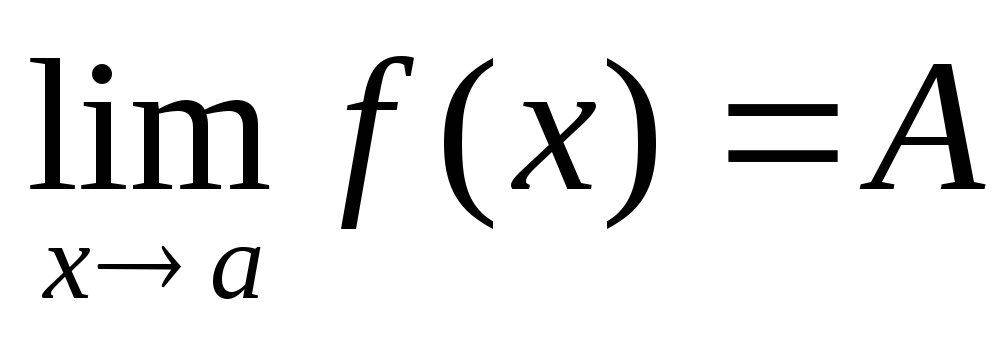 ,
где A
– конечное число, то на некоторой
окрестности U(a)
функция f(x)
ограничена, т.е. существует
положительное число М
такое, что
,
где A
– конечное число, то на некоторой
окрестности U(a)
функция f(x)
ограничена, т.е. существует
положительное число М
такое, что
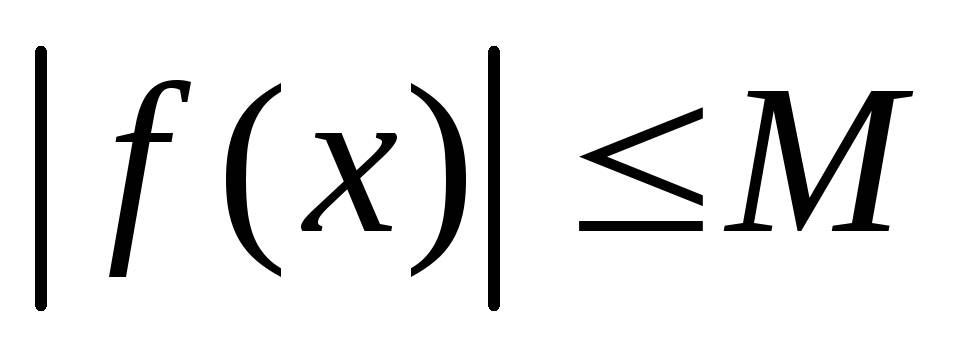 для всех
для всех ,.
,.Доказательство. Из условия теоремы следует существование окрестности U(a), такой, что
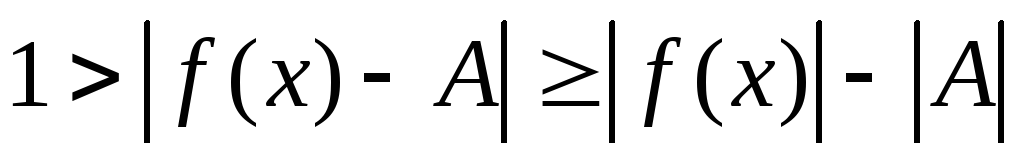
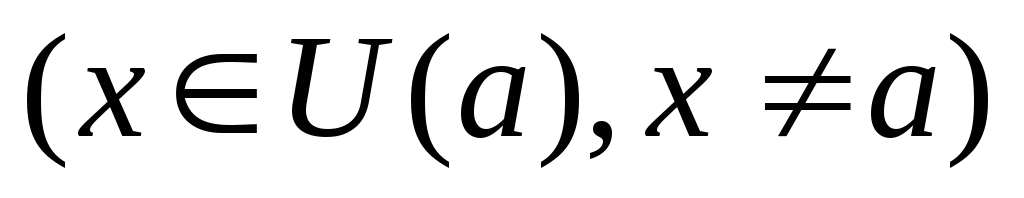 .
Отсюда для указанных х
.
Отсюда для указанных х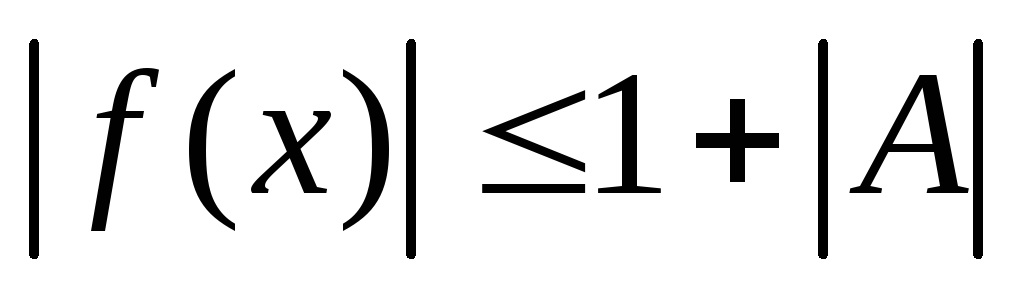 ,
где надо считать
,
где надо считать
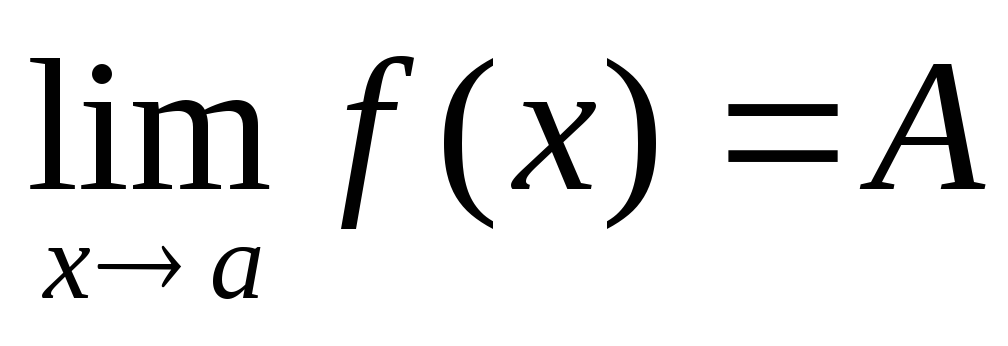 .
Теорема доказана.
.
Теорема доказана.Функция f, для которой
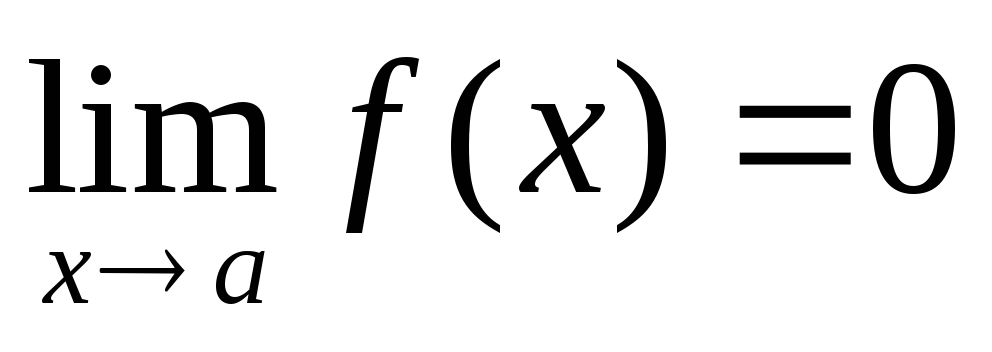 ,
называется бесконечно
малой при
,
называется бесконечно
малой при
 .
.-
Свойства бесконечно малых функций. Предел суммы, произведения и частного. Переход к пределу в неравенствах, предел промежуточной функции.
Функция называется бесконечно малой в точке x0, если предел ёё в этой точке равен нолю. Функция называется бесконечно большой в точке x0, если её предел в этой точке равен бесконечности.
Св-ва б.м.ф.:
1) Если функция f(x) ограничена, а m(x) бесконечно большая, то
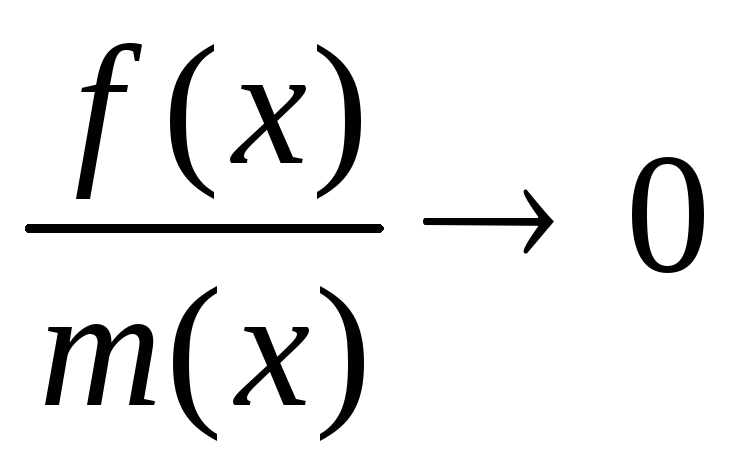
2) Если абсолютная величина f(x) ограничена снизу положительным числом, а m(x) не равная нулю бесконечно мала, то
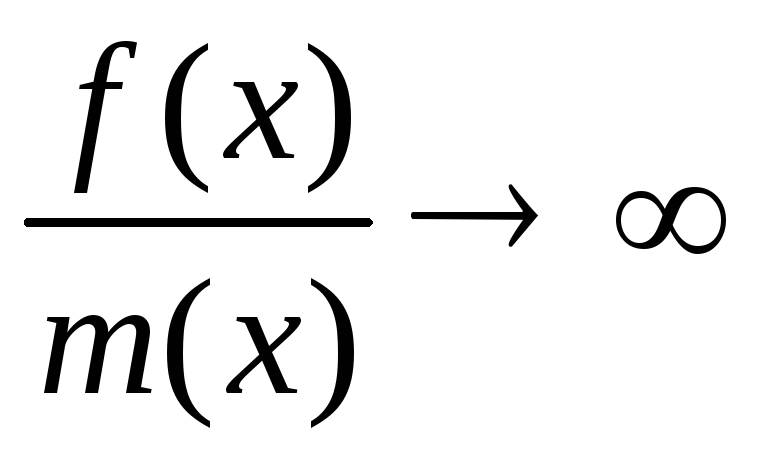
Предел суммы равен сумме пределов, предел произведения равен произведению пределов, предел частного равен частному пределов в том случае, если предел знаменателя не равен нулю.
Теорема. Если
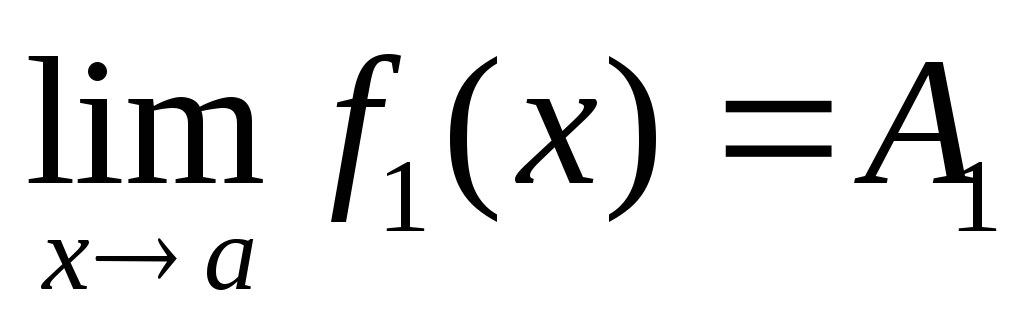 ,
,
 и на некоторой окрестности U(a),
и на некоторой окрестности U(a),
 ,
,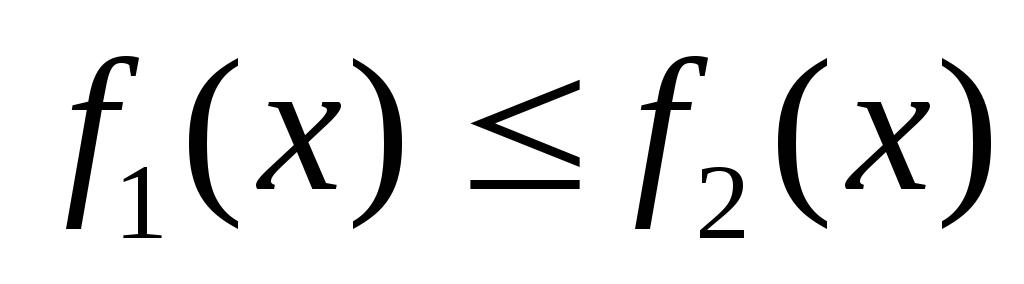 ,
то
,
то
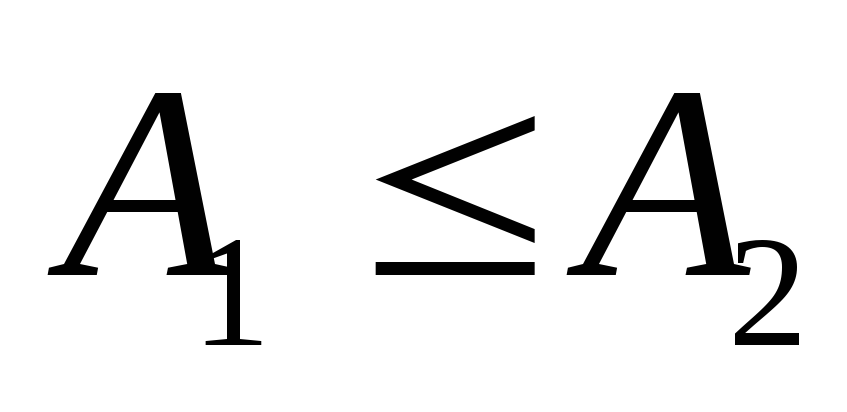 .
Доказательство.
Пусть
.
Доказательство.
Пусть
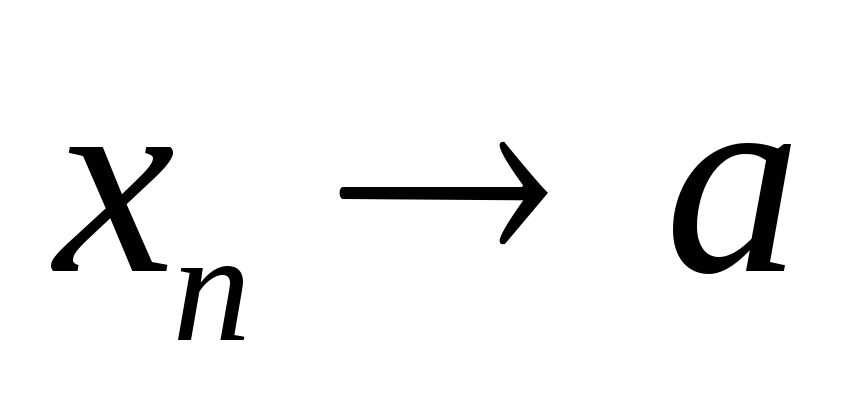 ,
,
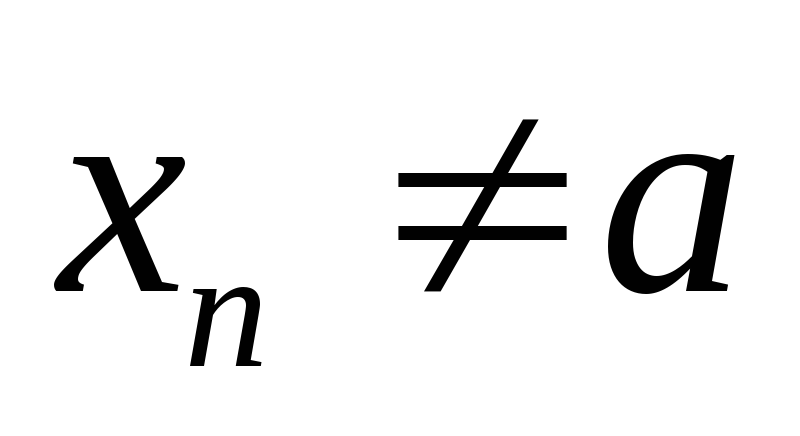 ;
тогда для достаточно большого n0
имеет
место неравенство
;
тогда для достаточно большого n0
имеет
место неравенство
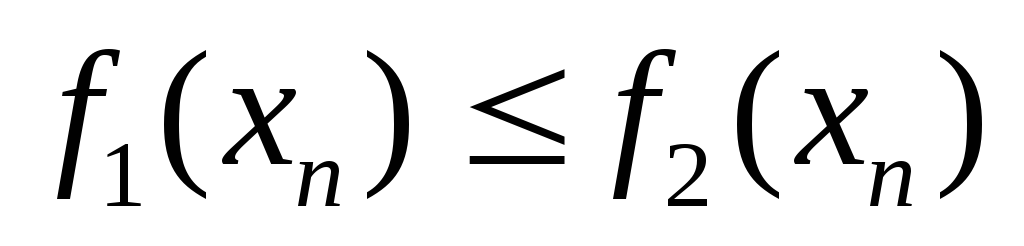
 и
после перехода к пределу неравенство
и
после перехода к пределу неравенство
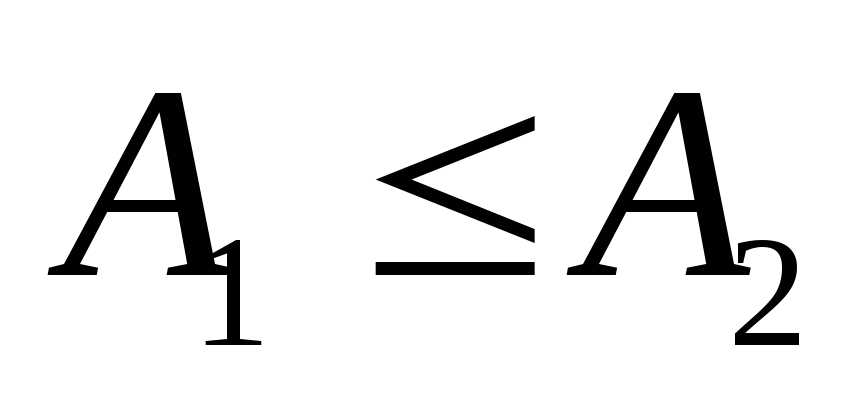 .
.Теорема .Если
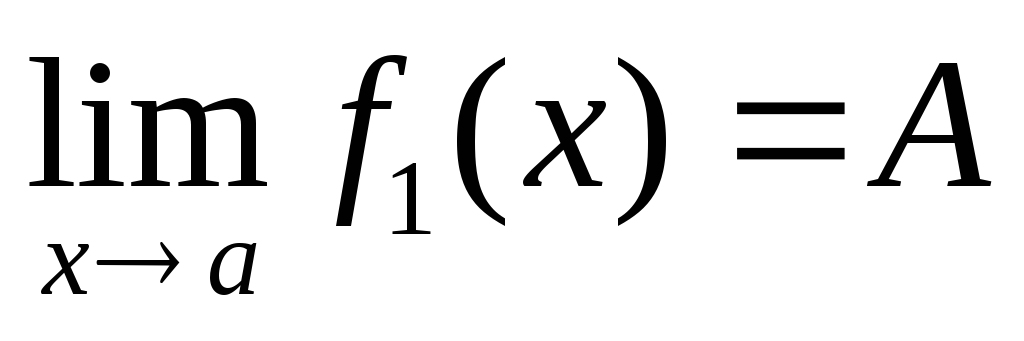 ,
,
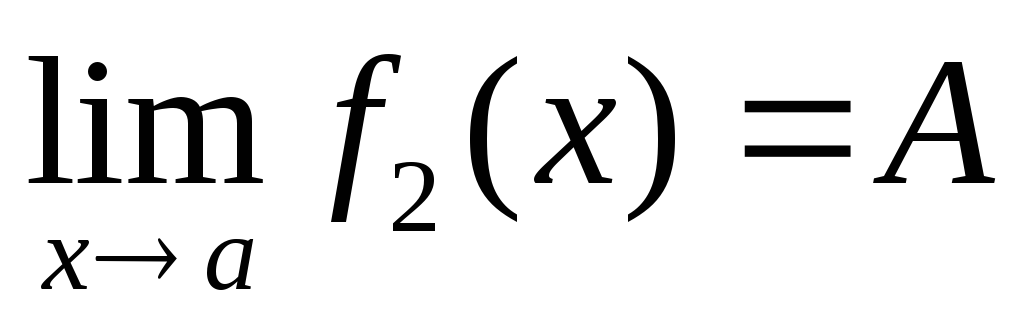 (1)
(1)и на некоторой окрестности U(a),
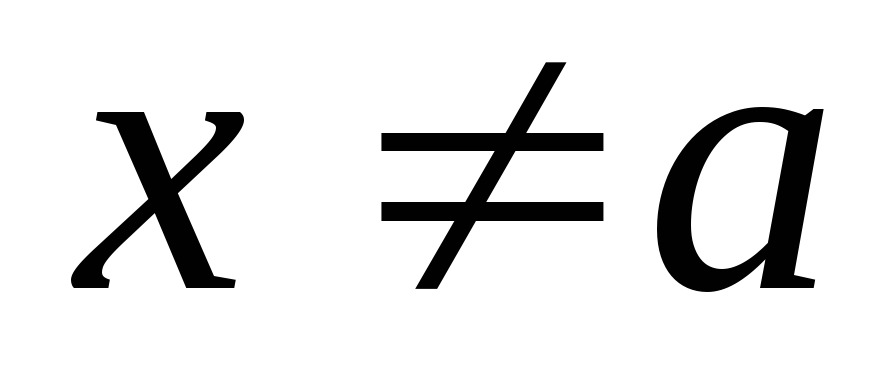 ,
,
 то
то
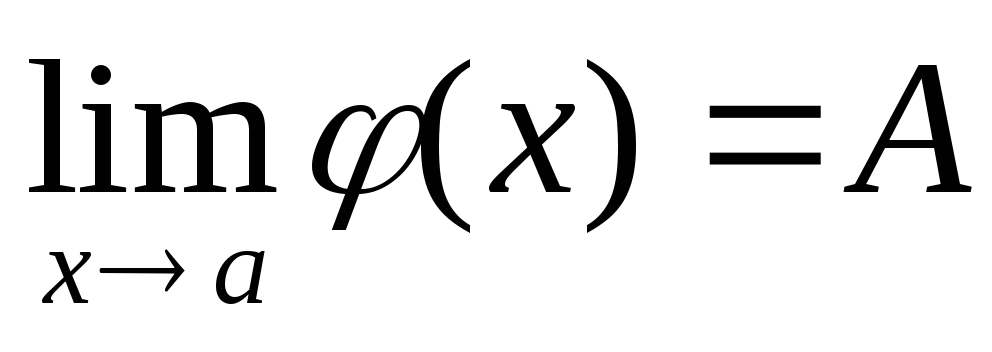 .
(2)
.
(2)Доказательство. Пусть
 ,
,
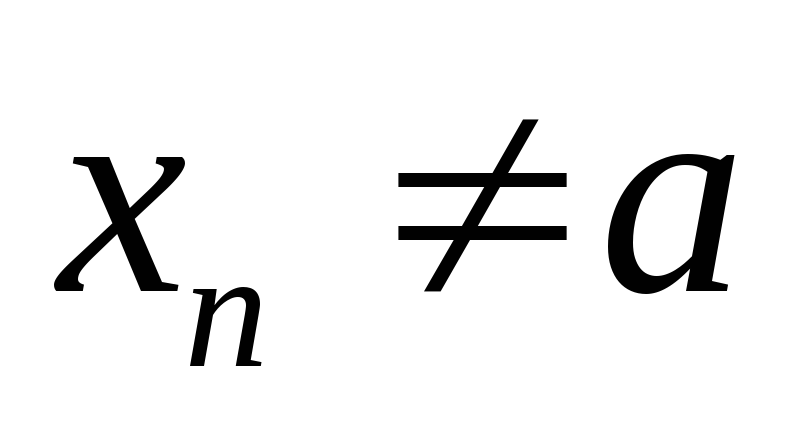 ;
тогда при достаточно большом
n0
для
;
тогда при достаточно большом
n0
для
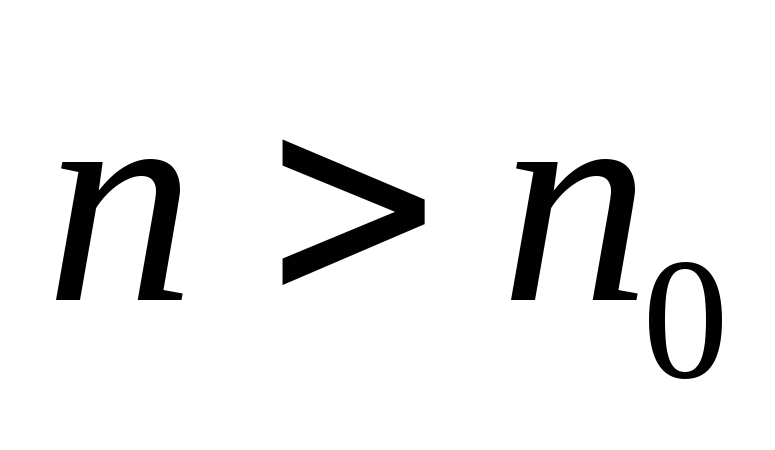
 и в силу (1)
существует предел
и в силу (1)
существует предел
 ,
равный А,
а так как {xn}
есть произвольная сходящаяся к а
последовательность, то имеет место
(2).
,
равный А,
а так как {xn}
есть произвольная сходящаяся к а
последовательность, то имеет место
(2).-
Непрерывность функции в точке. Свойства непрерывных функций. Асимптотическое разложение непрерывной функции.
Функция f(x) называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки, в том числе в самой точке х0, и если её приращение в этой точке, соответствующее приращению аргумента
 ,
стремится к нулю при
,
стремится к нулю при
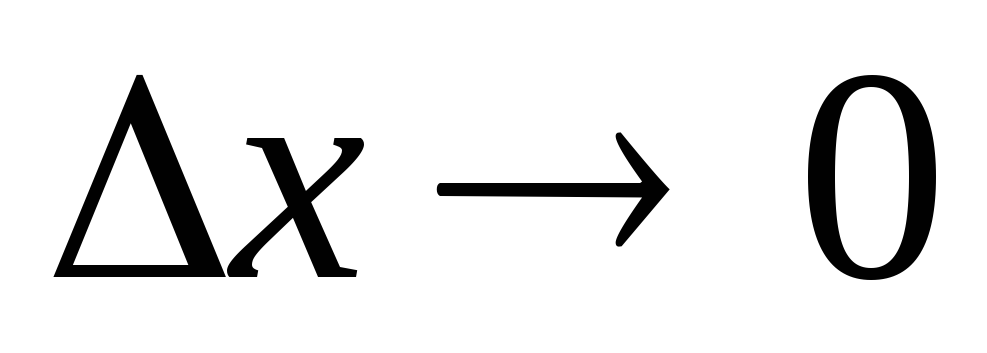 :
:
 .
.КОРОЧЕ:
 .
.Св-ва непрерывных ф-ций:
1. Если ф-ция y=f(x) непрерывна на [a,b] и f(a)*f(b)<0, т.е. знаки f(a) и f(b) противоположны, то на (a,b) найдется хотя бы одна точка х=с, что f(c)=0 (график)-теорема Больцана-Коши.
2. Если ф-ция y=f(x) непрерывна на [a,b], то она ограничена на этом промежутке.
3. Если ф-ция y=f(x) непрерывна на [a,b], то она достигает на этом отрезке min m и max M (теорема Вейерштрасса).
в точке:
1. если ф-ция f(x) и g(x) непрерывна в х0, то их сумма, произведение, частное (при (х0)0) явл-ся ф-циями, непрерывными в х0
2. если ф-ция y=f(x) непрерывна в х0, и f(x0)>0, то существует окрестность х0, в которой f(x)>0
3. если y=f(U) непрерывна в U0, а U=(x) непрерывна в U0=(x0), то сложная ф-ция y=f[(x)] непрерывна в х0.
-
Эквивалентные б.м.ф. Таблица эквивалентных б.м. функций. Замена отношения бесконечно малых эквивалентными при вычислении пределов.
Эквивалентными (асимптотически равными) называют функции (x) и (x) (обе стремящиеся к нулю), если выполняется свойство
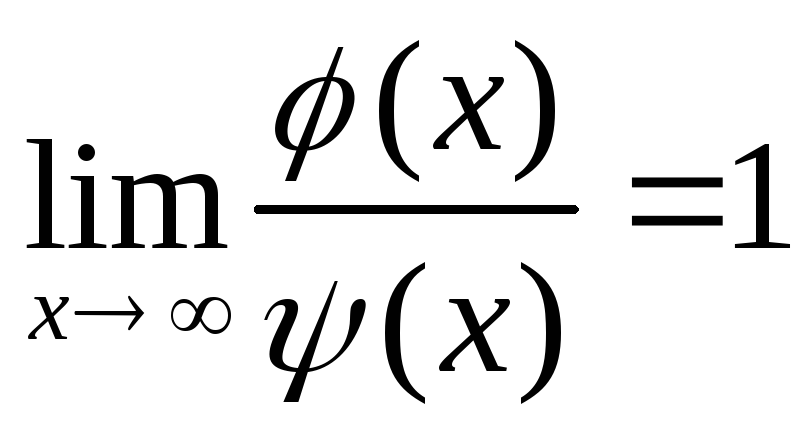 .
.Если b(x) и c(x) – эквивалентные б.м.ф. при
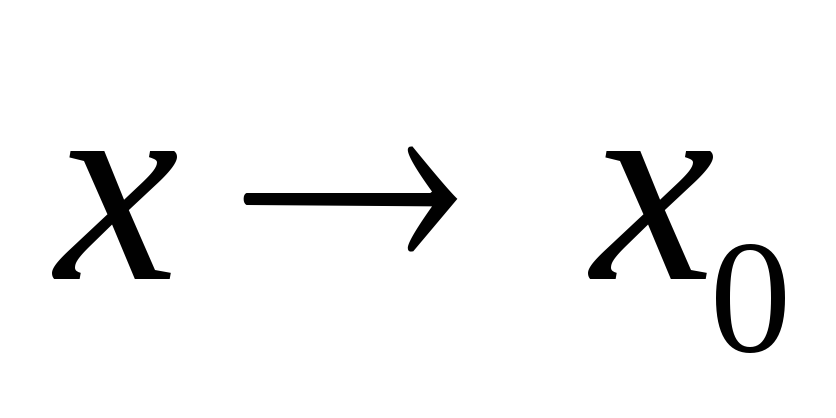 ,
тогда
,
тогда
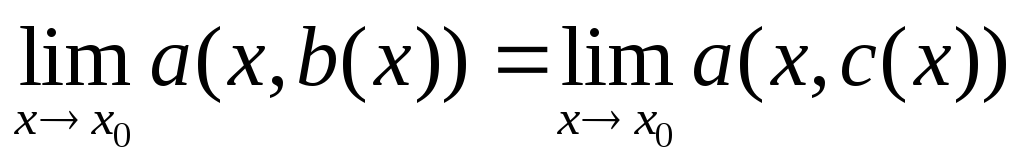 .
.-
Сравнение б.м.ф. Б.б.ф., связь с б.м.ф. Вертикальная асимптота графика функции.
Если функции (x )и (x), участвующие в
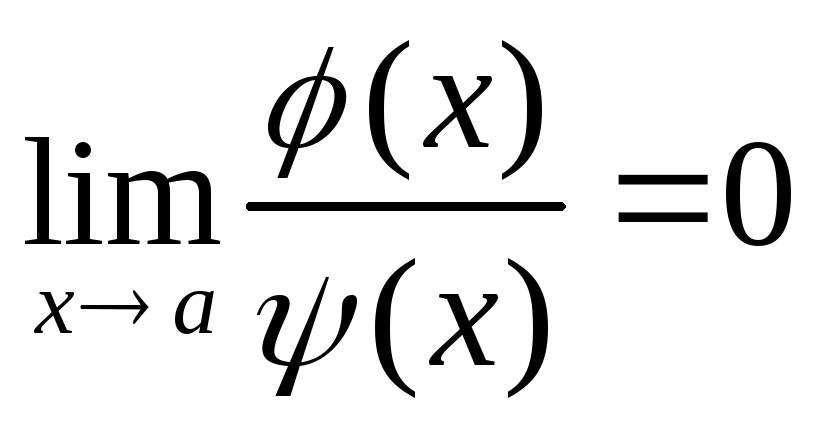 ,
суть бесконечно малые при
,
суть бесконечно малые при
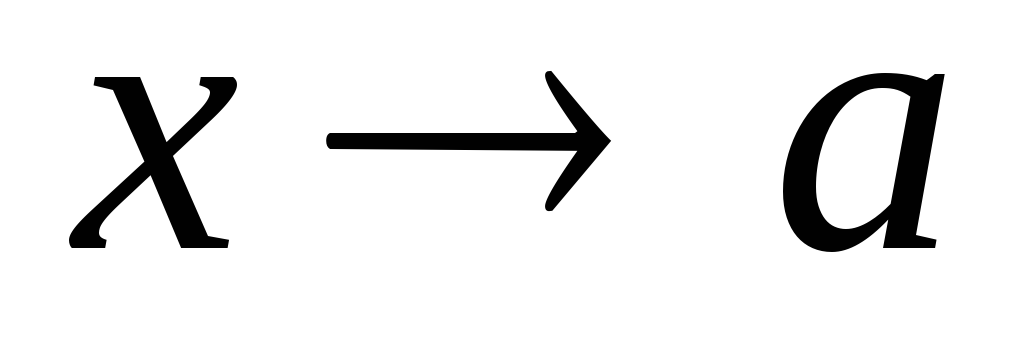 ,
то (x)
при
,
то (x)
при
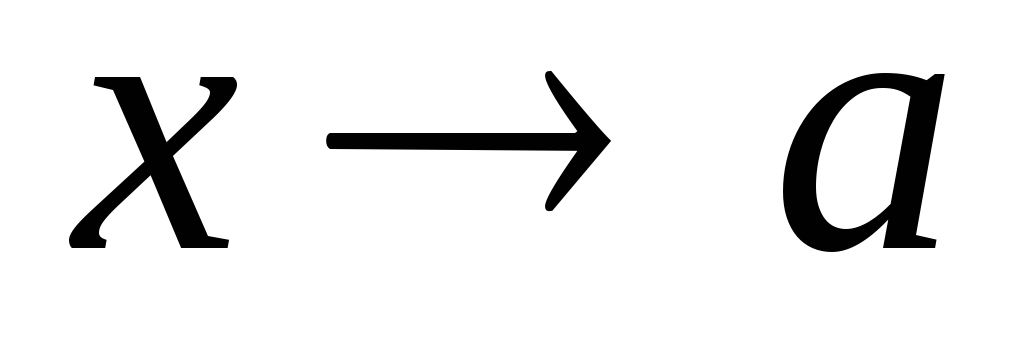 есть бесконечно малая высшего
порядка по отношению к (бесконечно
малой) (x)
(если же
это были бесконечно большие, то
(x)
более низкого порядка, чем (x).
есть бесконечно малая высшего
порядка по отношению к (бесконечно
малой) (x)
(если же
это были бесконечно большие, то
(x)
более низкого порядка, чем (x).Теорема о связи ббф и бмф. Пусть функция f(x)-бб при
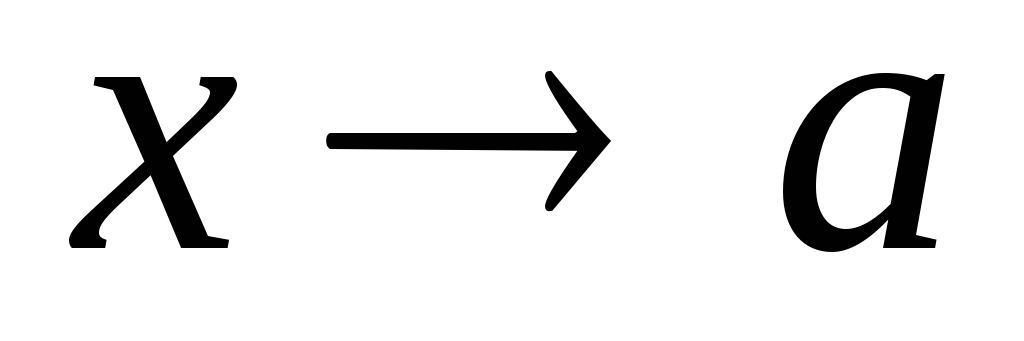 .
Тогда
функция a(x)
–бм при
.
Тогда
функция a(x)
–бм при

Доказательство (?).
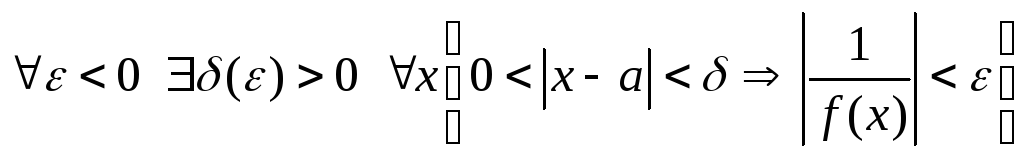 .
.Прямая х=а называется вертикальной асимптотой графика функции y=f(x), если хотя бы одно из предельных значений
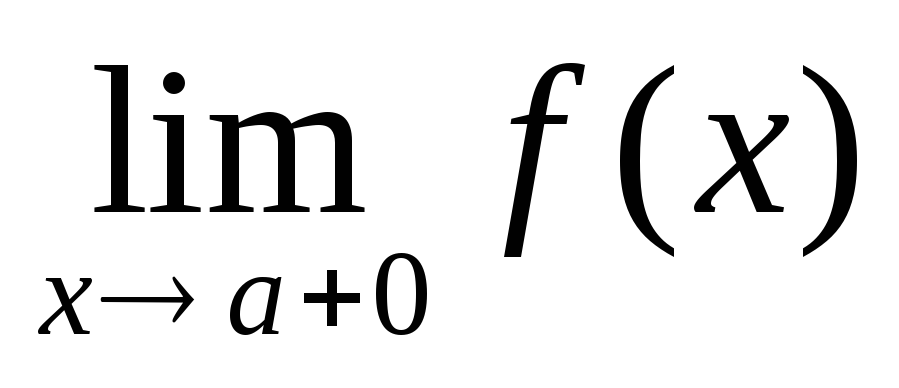 ;
;
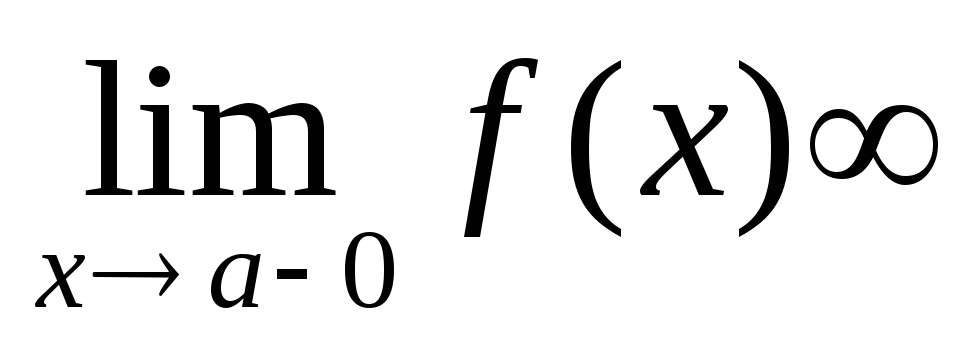 равно +
равно + или –
или – .
.-
Односторонние пределы. Классификация точек разрыва.
Число А называется пределом функции f(x) в точке x=a справа (при
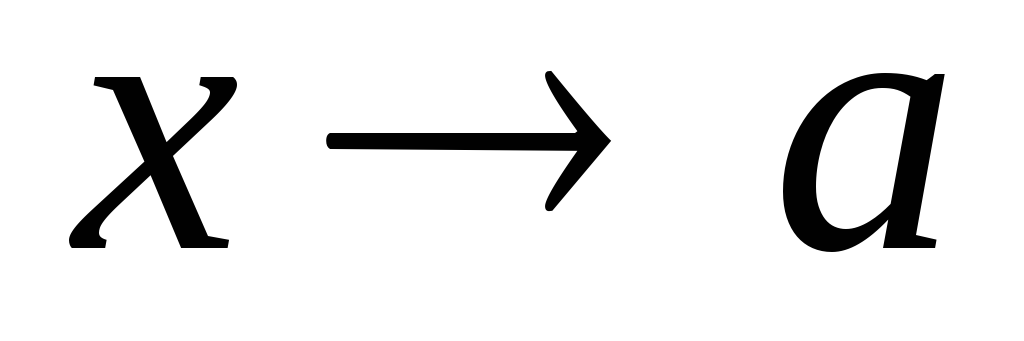 +0),
если
+0),
если .
.Точки, в которых функция f(x) не является непрерывной, называются точками разрыва для функции f(x). Если в точке x=a существуют пределы f(a+0), f(a–0), но неравенство
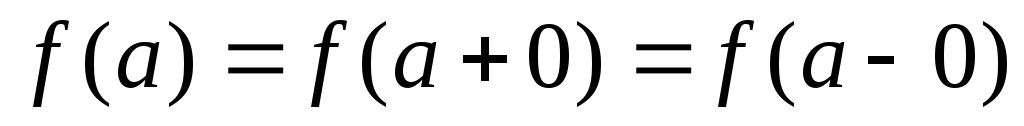 не выполняется,
не выполняется, то
точка х=а
называется точкой разрыва первого
рода для функции f(x).
Причём, если
то
точка х=а
называется точкой разрыва первого
рода для функции f(x).
Причём, если
 ,
то точка x=a
называется точкой устранимого
разрыва для функции f(x).
Если же в точке x=a
у функции f(x)
не существует правого или левого
предела или же эти пределы бесконечны,
то функция f(x)
имеет в точке x=a
разрыв второго рода.
,
то точка x=a
называется точкой устранимого
разрыва для функции f(x).
Если же в точке x=a
у функции f(x)
не существует правого или левого
предела или же эти пределы бесконечны,
то функция f(x)
имеет в точке x=a
разрыв второго рода.
-
Предел функции в бесконечности. Наклонная асимптота графика функции. Горизонтальная асимптота график функции.
Число А называется пределом функции f(x) при
 ,
если для произвольного числа
,
если для произвольного числа
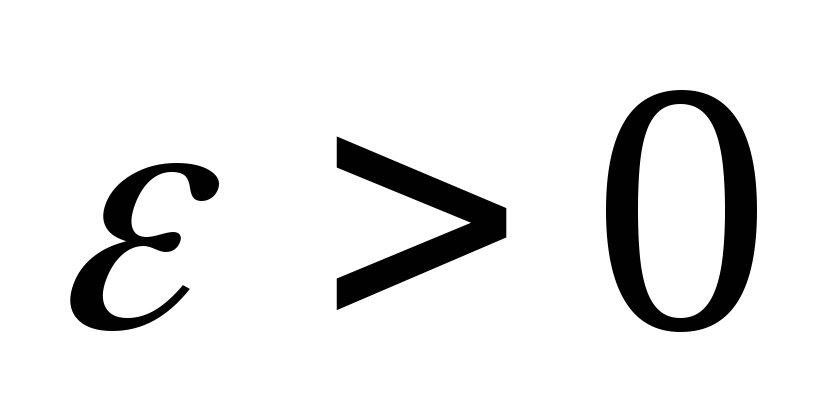 найдётся число N>0
(зависящее от ) такой, что для всех
значений x,
удовлетворяющих неравенству
найдётся число N>0
(зависящее от ) такой, что для всех
значений x,
удовлетворяющих неравенству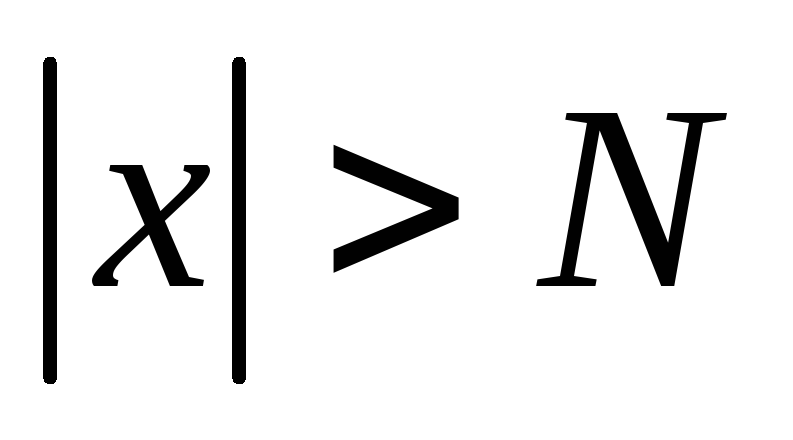 ,
будет иметь место неравенство
,
будет иметь место неравенство
 .
.Прямая Y=kx+b называется наклонной асимптотой графика функции y=f(x) при
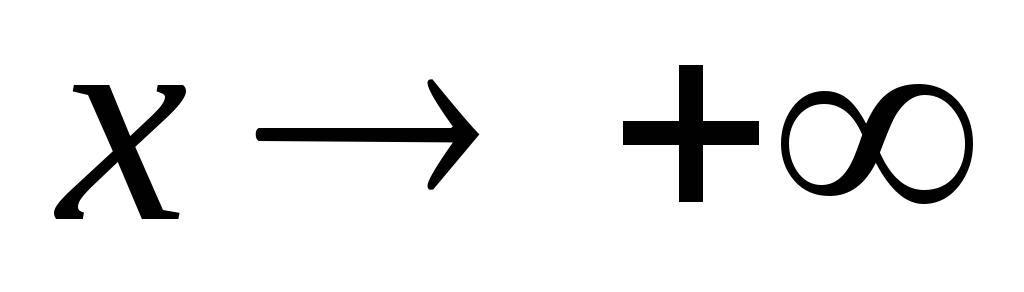 ,
если функция f(x)
представлена в виде
,
если функция f(x)
представлена в виде
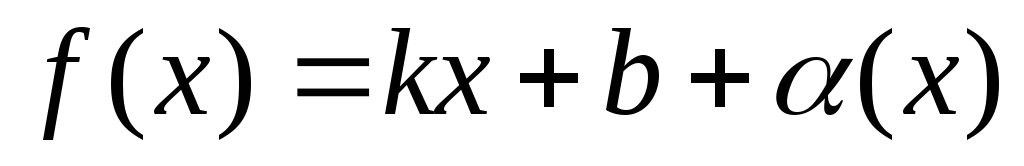 ,
где (x)=o(1)
(
,
где (x)=o(1)
(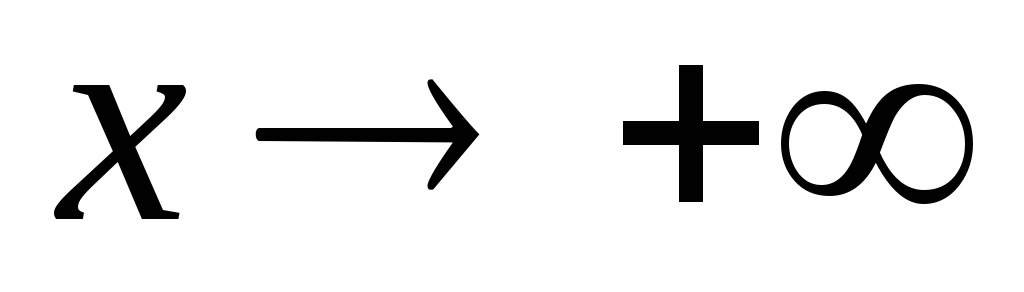 ).
Если коэффициент k=0
т.е. уравнение наклонной асимптоты
имеет вид Y=b,
то тогда её называют горизонтальной
асимптотой. НО для того, чтобы график
функции y=f(x)
имел при
).
Если коэффициент k=0
т.е. уравнение наклонной асимптоты
имеет вид Y=b,
то тогда её называют горизонтальной
асимптотой. НО для того, чтобы график
функции y=f(x)
имел при
 наклонную асимптоту, необходимо и
достаточно, чтобы существовали два
предельных значения
наклонную асимптоту, необходимо и
достаточно, чтобы существовали два
предельных значения
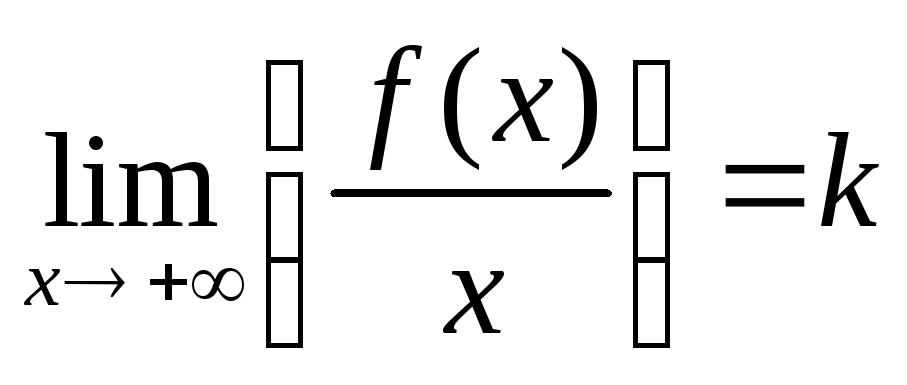 и
и
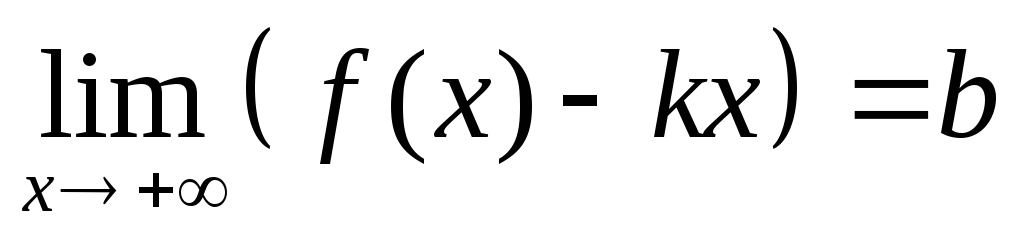 .
.-
Производная. Геометрический и механический смысл производной. Уравнение касательной и нормали к графику функции.
П
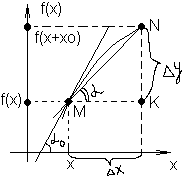 роизводной
функции f(x)
в точке
x
называется предел её приращения
роизводной
функции f(x)
в точке
x
называется предел её приращения
 в этой точке к соответствующему
приращению аргумента
в этой точке к соответствующему
приращению аргумента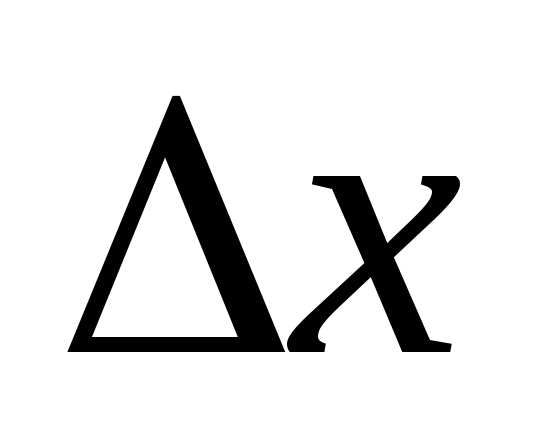 ,
когда
,
когда
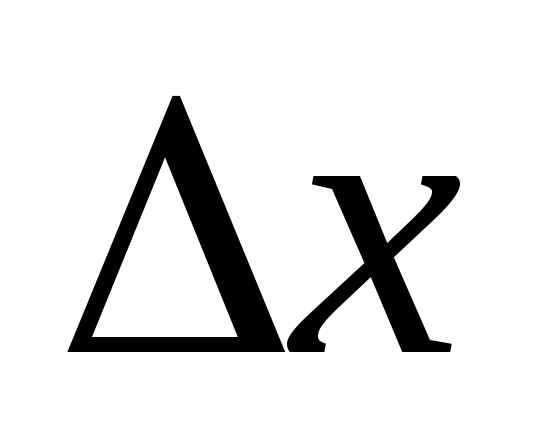 стремиться к нулю (при условии, что
этот предел существует). Для
обозначения производной используют
символы
стремиться к нулю (при условии, что
этот предел существует). Для
обозначения производной используют
символы
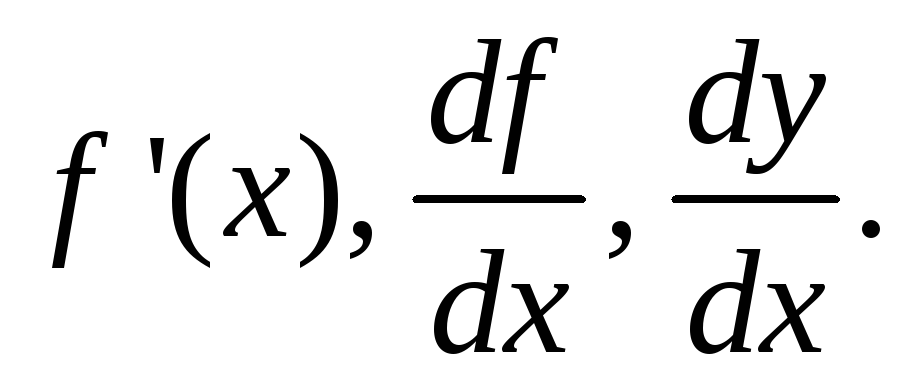 Определение записывается и таким
образом
Определение записывается и таким
образом
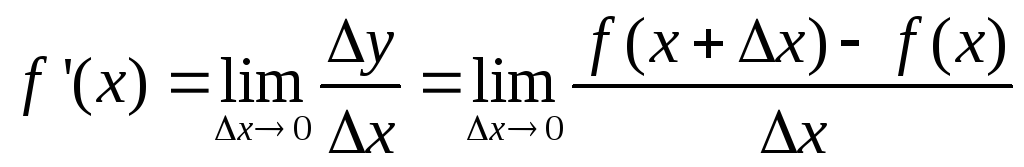 .
.
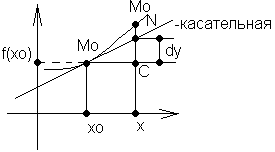
Геометрический смысл производной заключается в том, что есть tg угла наклона касательной, проведенной в точке x0. KN=y, MK=x
tg угла KMN=y/x
вычислим предел левой и правой части:
limtg=lim(y/x) x0
tg0=y`
0
При x0 секущая MNзанять положение касательной в точке M(tg0=y`, 0).
Касательной Т к кривой y=f(x), проходящей через точку (x;f(x)), называется предельное положение секущей при x0. Уравнение касательной в точке M(x0,f(x0)) записывается в виде
 .
.Нормалью к графику функции в точке M(x0,f(x0)) назовём прямую, проходящую через точку М и перпендикулярную касательной, проходящей через эту же точку.
-
Дифференцируемость функции. Дифференциал. Необходимое и достаточное условие дифференцируемости. Геометрический смысл дифференциала. Таблица производных.
Функция f(x) называется дифференцируемой в точке х, если её приращение
 в этой точке может быть представлено
в виде
в этой точке может быть представлено
в виде
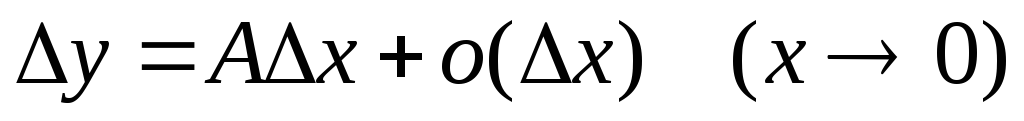 ,
где величина А не зависит от x.
,
где величина А не зависит от x.Теорема. Для того, чтобы функция f(x) была дифференцируемой в точке х, необходимо и достаточно, чтобы она имела в этой точке конечную производную. Тогда величина А из
 равна производной: A=f’(x).
равна производной: A=f’(x).Достаточность. Из существования производной выводим дифференцируемость
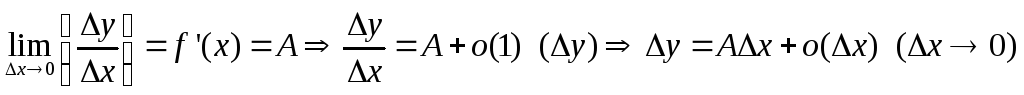
Необходимость. Из дифференцируемости функции выводим существование производной
 .
.Дифференциалом функции называют главную часть приращения в точке х, соответствующим приращению аргумента х. Дифференциал dy=Ax=f’(x)x или dy=f’(x)dx.
Геометрический смысл: дифференциал - изменение ординаты касательной, проведенной к графику ф-ции в точке (x0,f(x0)) при изменении x0 на величину x
Св-ва: 1. (UV)`=U`V`, то (UV)`dx=U`dxV`dx, d(UV)=d(UV)
2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV
3.d(c)=c`dx=0*dx=0
4. d(U/V)`=(V`dU-U`dV)/V2.
-
Непрерывность дифференцируемой функции. Производные суммы, произведения и частного. Производная сложной функции. Логарифмическая производная.
Теорема. Если функция f(x) дифференцируема в точке х, то f(x) непрерывна в точке x. Доказательство. Пусть функция f(x) дифференцируема в точке x, т.е. y=Ax+o(x) (x0). Тогда
 ,
т.е. функция f(x)
непрерывна в точке x.
,
т.е. функция f(x)
непрерывна в точке x.(f(x)+g(x))’=f’(x)+g’(x)
(f(x)*g(x))’=f’(x)*g(x)+f(x)* g’(x)
(cf(x))’=cf’(x)
(f(x)/g(x))’=(f’(x)*g(x)-f (x) * g’(x))/((g*g)(x))
Производная сложной ф-ции =произведению производной ф-ции по промежуточному аргументу и производной самого промежуточного аргумента по независимой переменной.
y`=f(x)*U`,или yx`=yU`*Ux`, или dy/dx=dy/dU=dU/dx
Если z=z(x) – дифференцируемая функция от x, то формулы имеют вид:
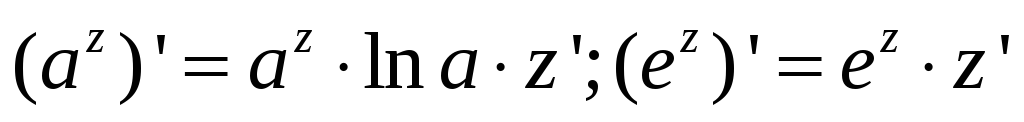
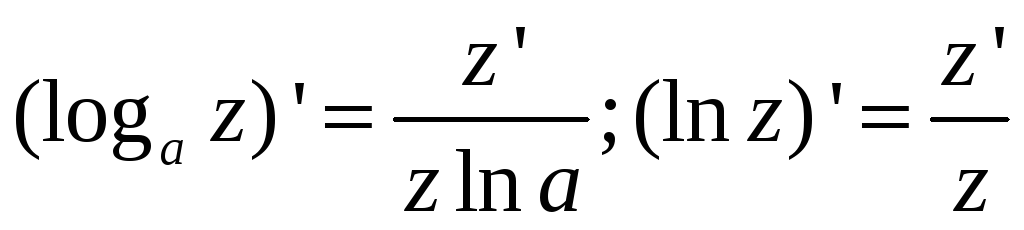
-
Производная обратной функции. Производные обратных тригонометрических функций.
y=f(x), то x=(y) - обратная ф-ция.
Для дифференцируемой ф-ции с производной, не = 0, производная обратной ф-ции = обратной величине производной данной ф-ции, т.е. xy`=1/yx`.
y/x=1/(x/y) - возьмем предел от левой и правой части, учитывая, что предел частного = частному пределов:
lim(y/x)=1/(lim(x/y), т.е. yx`=1/xy или f`(x)=1/`(f(x))
Основные формулы:
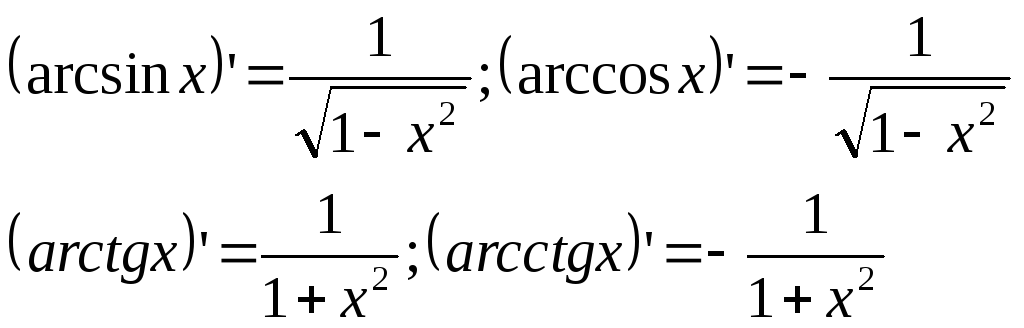
Для сложных функций:
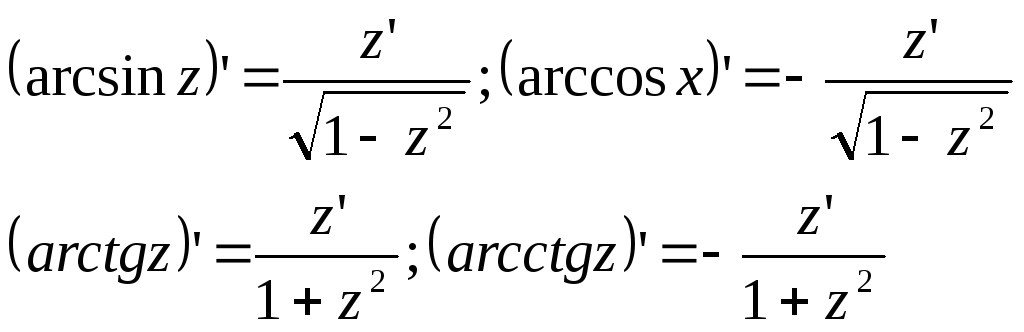
-
Производные и дифференциалы высших порядков.
y=f(x)
y``=(y`)`=lim((f`(x+x)-f`(x))/x)
x0
y```=(y``)`= lim((f``(x+x)-f``(x))/x)
f(n)(x)=[f(n-1)(x)]`
dsinx=cosxdx
ddsinx=dcosxdx=-sinxdxdx
d2sinx=-sinxdx2
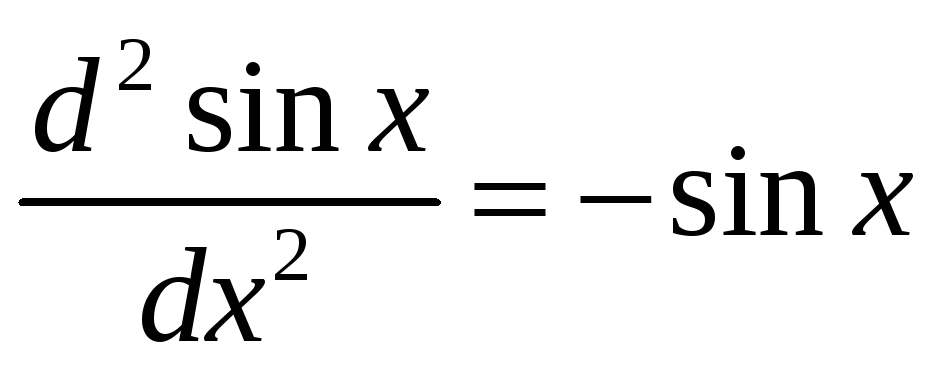
-
Функции, непрерывные на отрезке. Свойства функций, непрерывных на отрезке.
Функция непрерывна на отрезке, если она непрерывна в каждой точке этого отрезка.
1
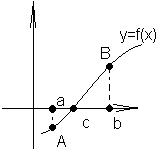 .
Если ф-ция y=f(x)
непрерывна на [a,b]
и f(a)*f(b)<0,
т.е. знаки f(a)
и f(b)
противоположны, то на (a,b)
найдется хотя бы одна точка х=с,
что f(c)=0
(график)-теорема Больцана-Коши.
.
Если ф-ция y=f(x)
непрерывна на [a,b]
и f(a)*f(b)<0,
т.е. знаки f(a)
и f(b)
противоположны, то на (a,b)
найдется хотя бы одна точка х=с,
что f(c)=0
(график)-теорема Больцана-Коши.2. Если ф-ция y=f(x) непрерывна на [a,b], то она ограничена на этом промежутке.
3. Если ф-ция y=f(x) непрерывна на [a,b], то она достигает на этом отрезке min m и max M (теорема Вейерштрасса).
в точке:
1. если ф-ция f(x) и g(x) непрерывна в х0, то их сумма, произведение, частное (при (х0)0) явл-ся ф-циями, непрерывными в х0
2. если ф-ция y=f(x) непрерывна в х0, и f(x0)>0, то существует окрестность х0, в которой f(x)>0
3. если y=f(U) непрерывна в U0, а U=(x) непрерывна в U0=(x0), то сложная ф-ция y=f[(x)] непрерывна в х0.
-
Основные теоремы дифференциального исчисления (Ролля, Лагранжа, Коши), их геометрический смысл.
Теорема Ролля.
Если функция f(x) непрерывна на заданном промеж/ [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует т. с из интерв. (a,b), такая, что f’(c)=0.
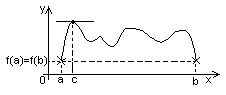
Теорема Лагранжа.
Если функция f(x) непрерывна на [a,b] и дифференцирована на (a,b), то сущест.
т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).
Доказательство: применим т. Коши, взяв только g(x)=x, тогда g’(x)=10.
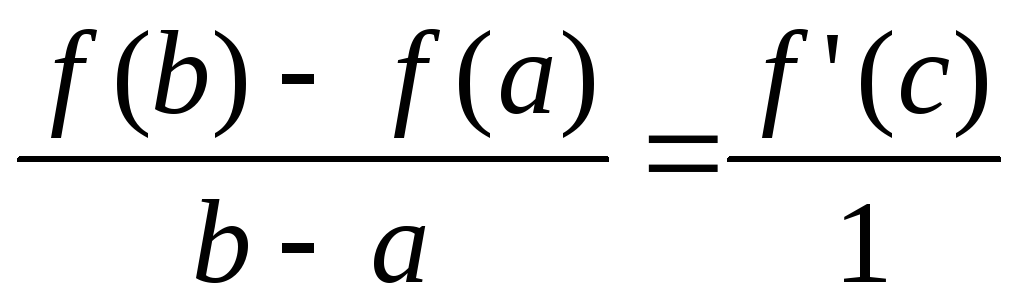

Теорема Коши.
Если f(x), g(x) удовл. трем условиям:
1). f(x), g(x) непрерыв. на промеж [a,b]
2). f(x), g(x) деффер. на интервале (a,b)
3). g’(x)0 на интер. (a,b), то сущ. т. с
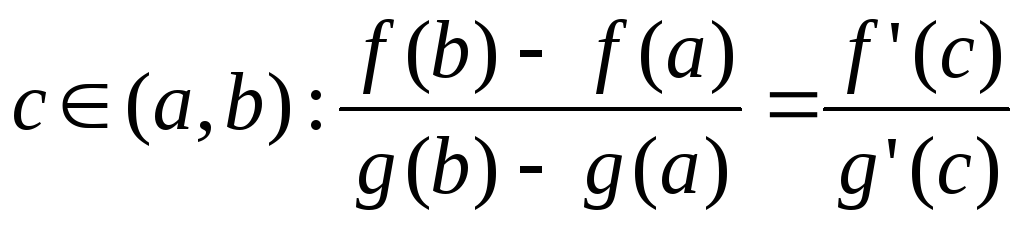
g(b)g(a) (неравны по теореме Ролля).
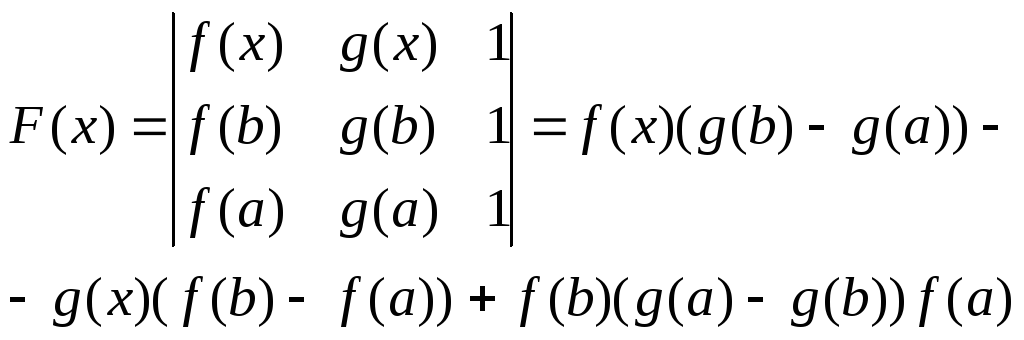
1). F(x) – непрерывна на [a,b]
2). F(x) – деффиренцирована на (a,b)
3). F(a)=0 ; F(b)=0
по теореме Ролля сущ. с(a,b); F’(с)=0

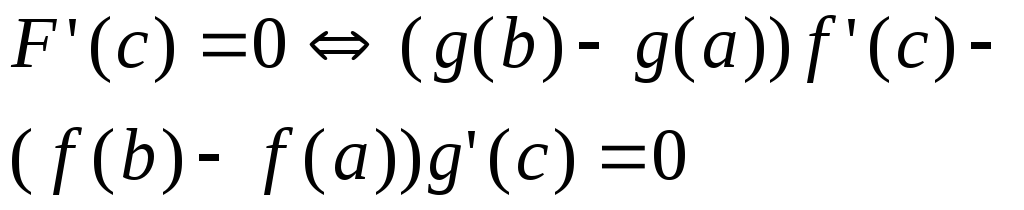

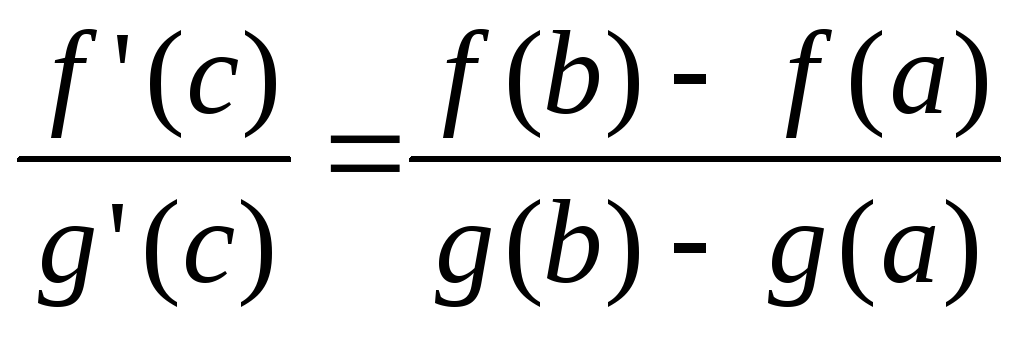
-
Правило Лопиталя для вычисления пределов.
Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой проколотой окрестности точки а. Пусть
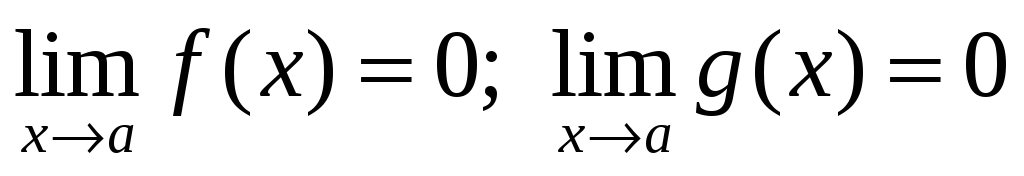 и
и
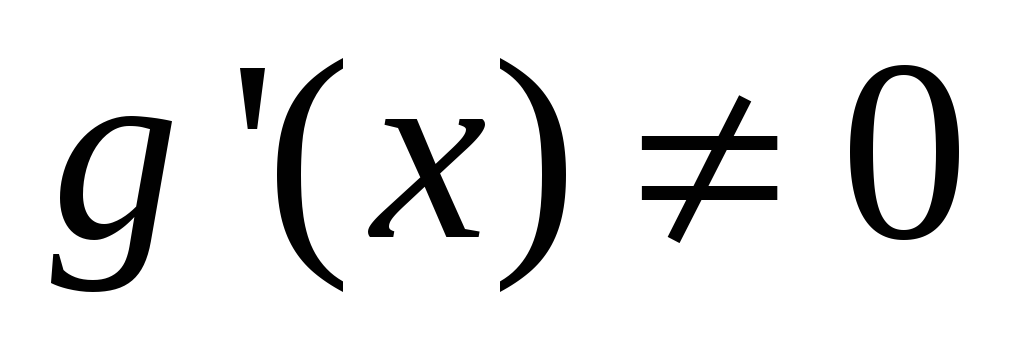 в указанной окрестности. Тогда,
если существует
в указанной окрестности. Тогда,
если существует
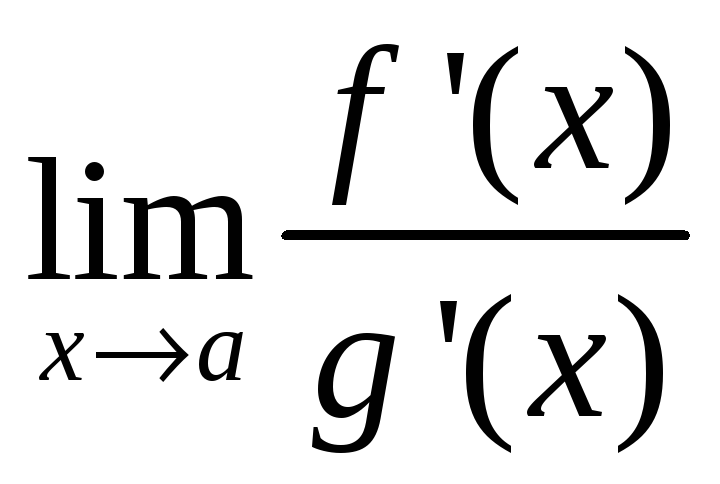 ,
то существует
,
то существует
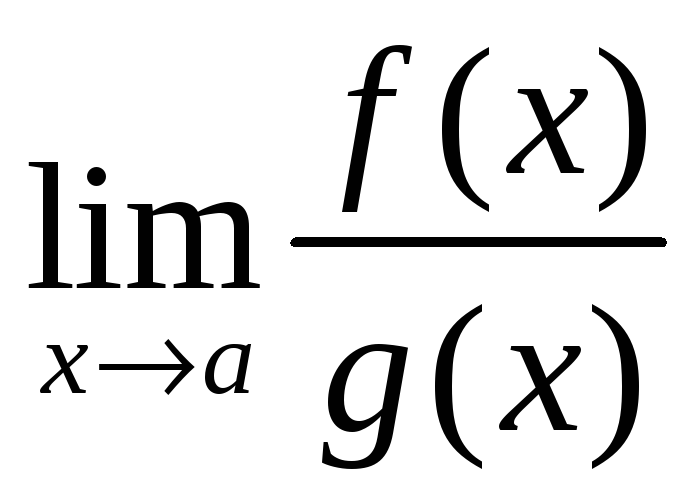 и имеет место равенство
и имеет место равенство
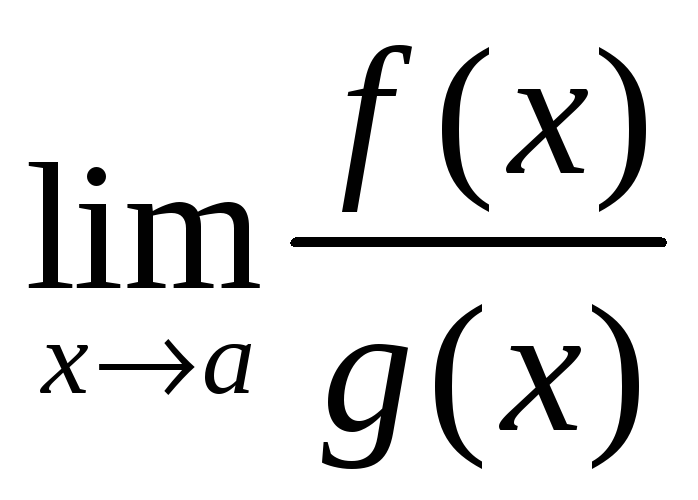 =
=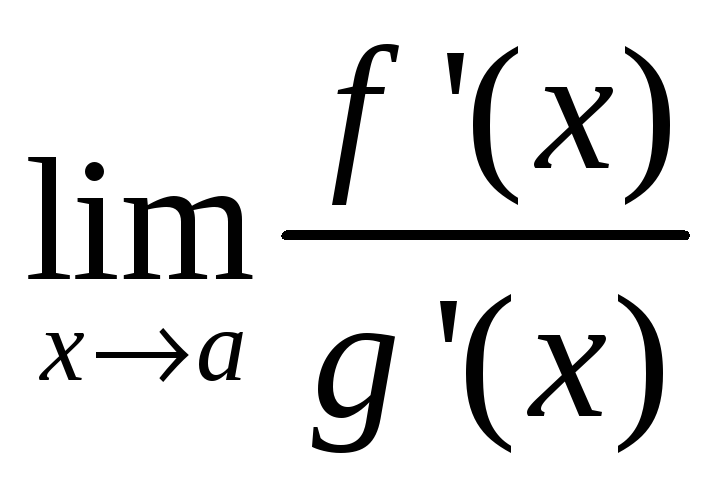 .
.Доказательство. Доопределим функции f(x) и g(x) при х=а: f(a)=0, g(a)=0. Тогда эти функции станут непрерывными в окрестности точки а.
Рассмотрим отрезок [а;х], если x>a и отрезок [x;a], если x<a, причём х принадлежит окрестности, о которой говориться в условии теоремы.
Для функций f(x) и g(x) на указанных отрезках выполнены условия теоремы Коши. Поэтому можно записать

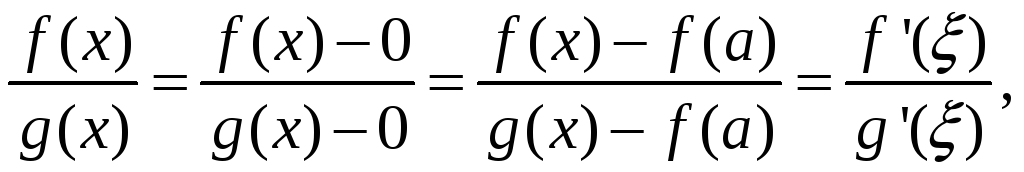 причём
причём
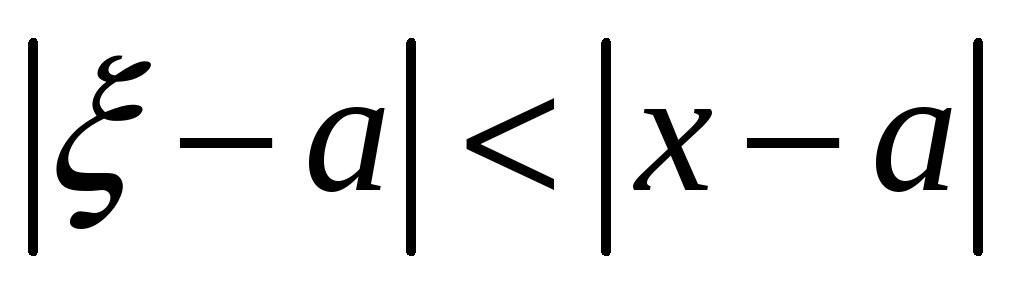 .
Поэтому, если
.
Поэтому, если
 ,
то и
,
то и
 .
Так как по условию теоремы существует
.
Так как по условию теоремы существует
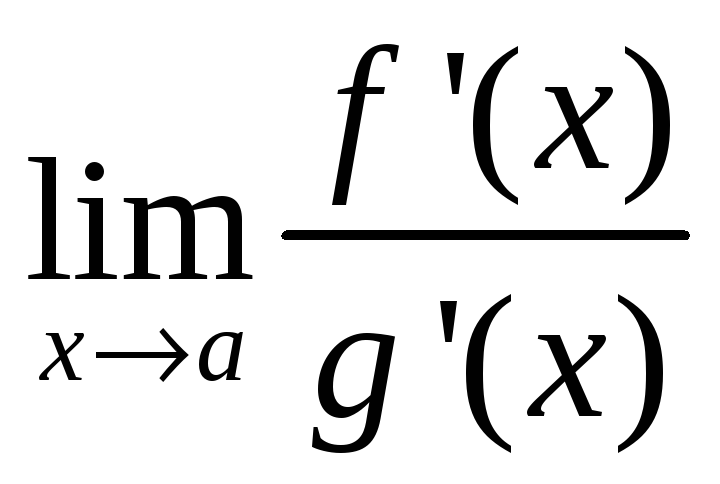 ,
то существует и
,
то существует и
 и эти пределы равны. Стало быть
и эти пределы равны. Стало быть
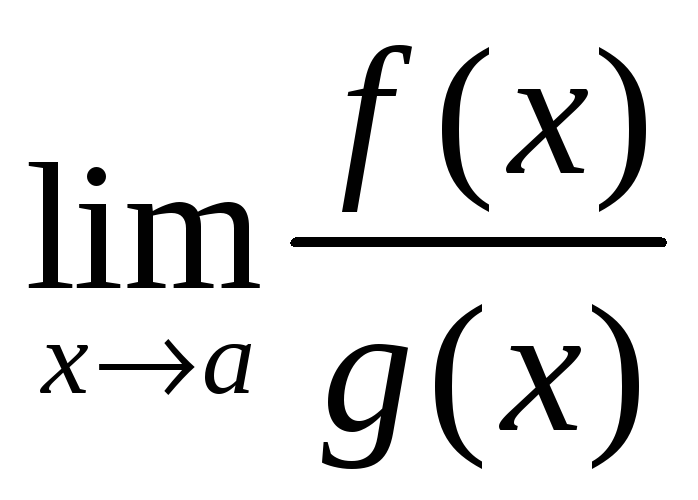 =
=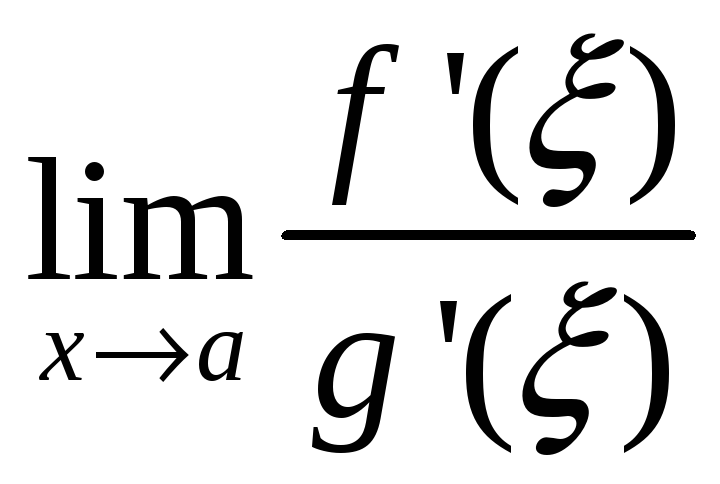 =
=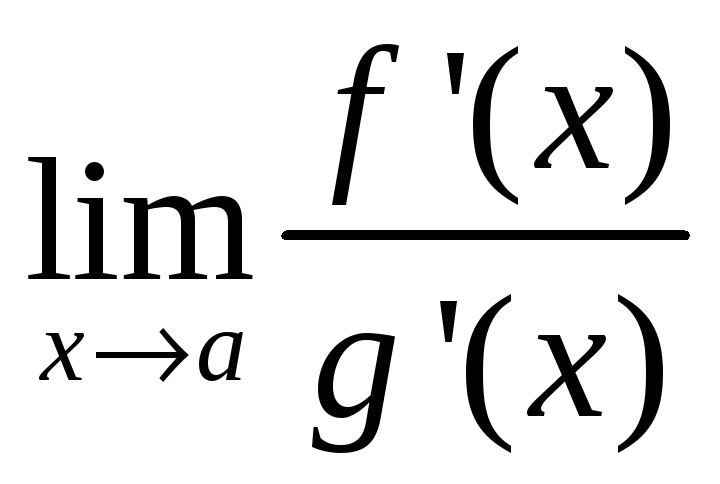 .
.-
Условие возрастания и убывания дифференцируемой функции на интервале.
Функция f(x) называется неубывающей на интервале (a;b), если для произвольных
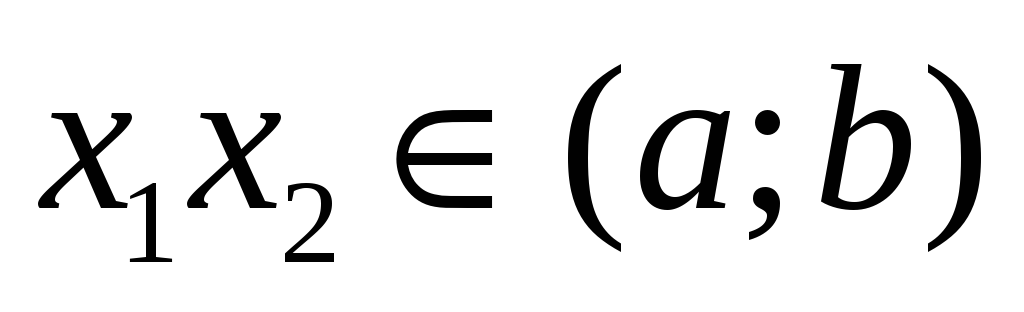 ,
удовлетворяющих условию x1<x2
справедливо неравенство
,
удовлетворяющих условию x1<x2
справедливо неравенство
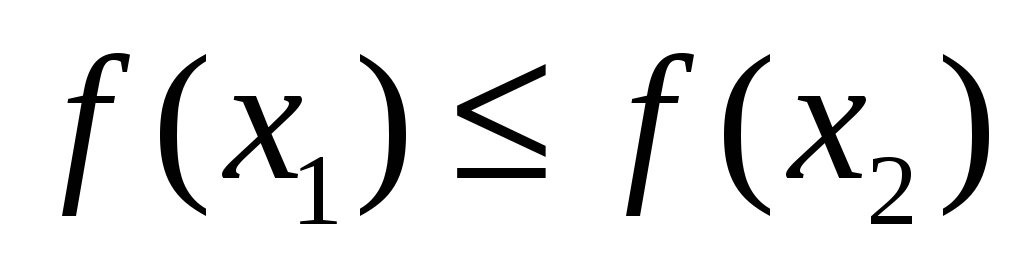 .
Аналогично определяется невозрастающая
функция.
.
Аналогично определяется невозрастающая
функция.
Теорема. Для того, чтобы дифференцируемая на интервале (a;b) функция f(x) не убывала на этом интервале, необходимо и достаточно, чтобы производная f’(x) была неотрицательной на этом интервале.
Доказательство. Необходимость. Пусть функция f(x) не убывает на (a;b), т.е. для любых
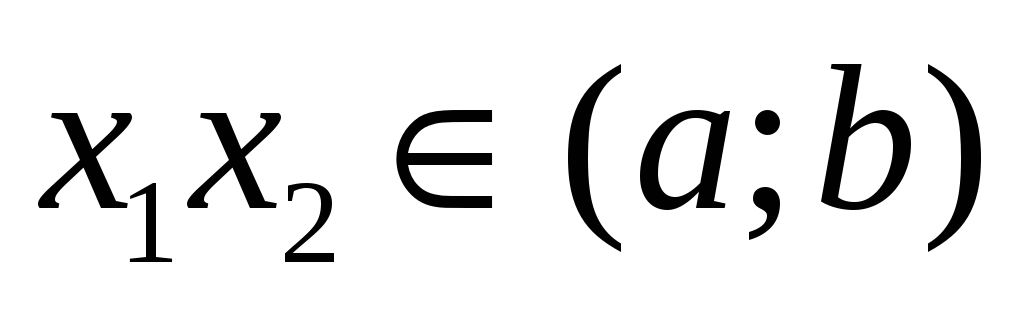 ,
удовлетворяющих условию
x1<x2
следует неравенство
,
удовлетворяющих условию
x1<x2
следует неравенство
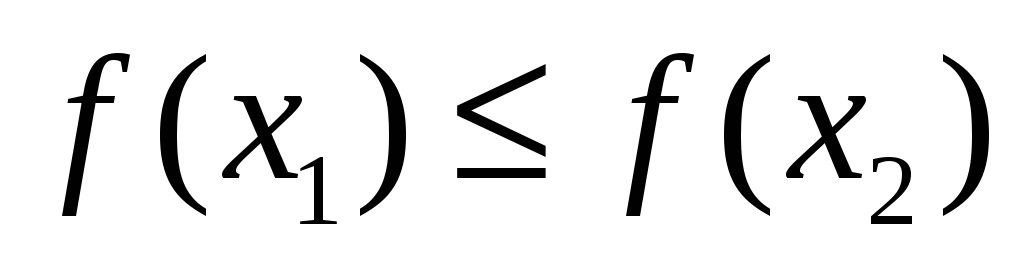 .
Пусть х
– любая
точка интервала (a;b),
дадим аргументу положительное
приращение Δх,
не выводящее его из интервала (a;b).
Тогда
.
Пусть х
– любая
точка интервала (a;b),
дадим аргументу положительное
приращение Δх,
не выводящее его из интервала (a;b).
Тогда
 ,
т.к.
,
т.к.
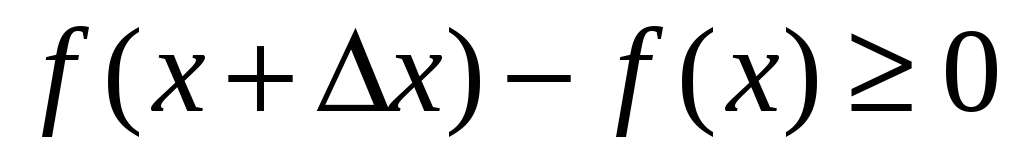 .
Поэтому
.
Поэтому
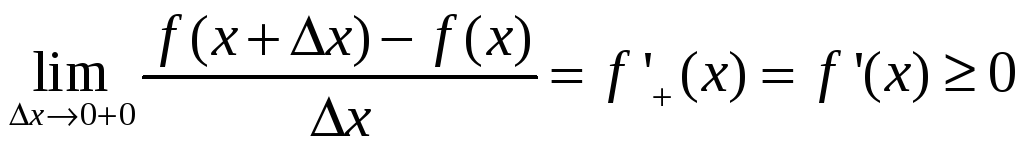 .
.Достаточность. Требуется доказать, что из условия
 на (a;b)
следует, что
на (a;b)
следует, что
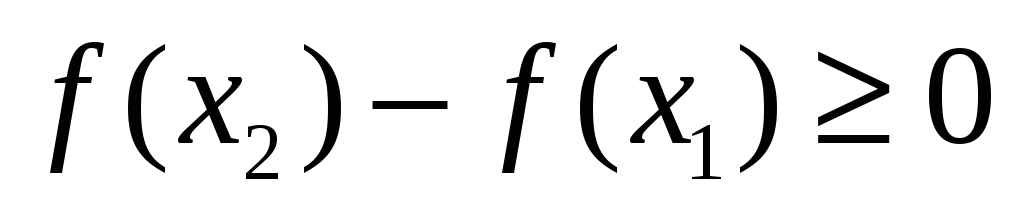 для любых
для любых
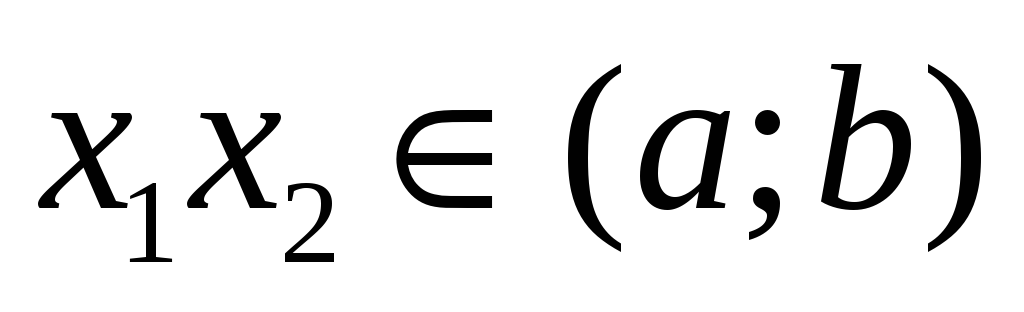 ,
удовлетворяющих условию
,
удовлетворяющих условию
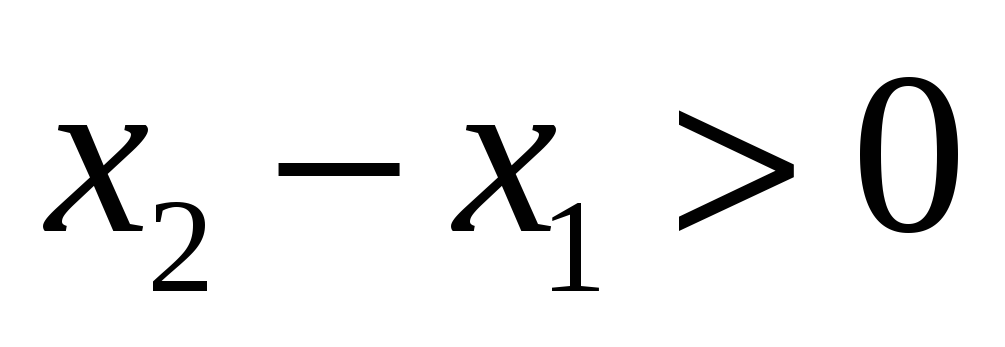 .
Применим теорему Лагранжа
.
Применим теорему Лагранжа
 ,
т.к.
,
т.к.
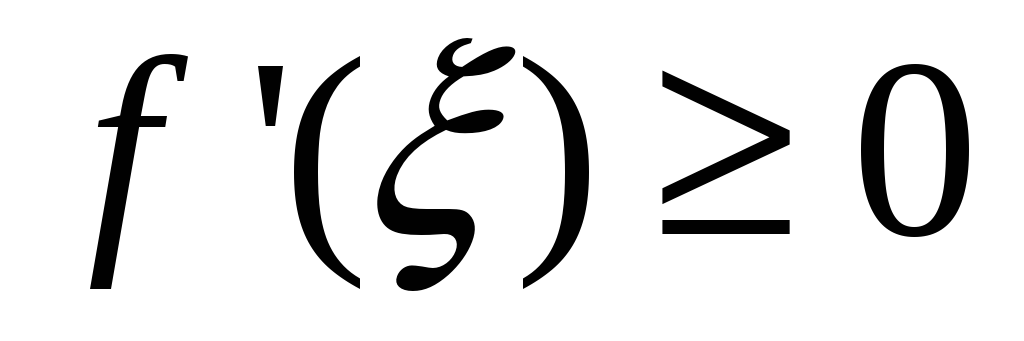 и
и
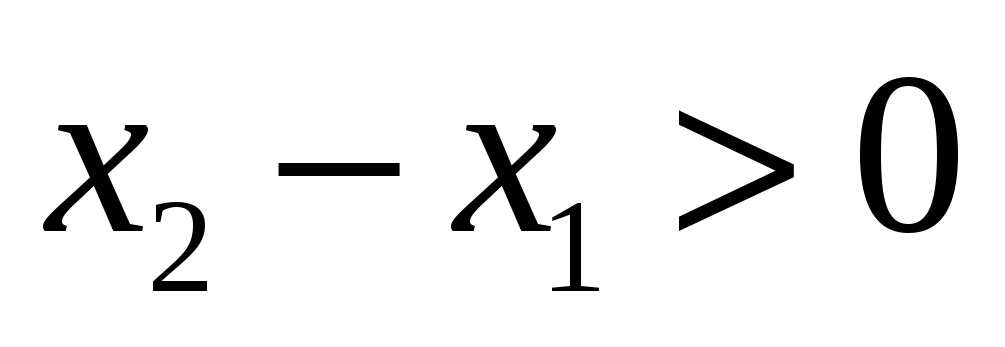
-
Э
 кстремумы
функции. Необходимые условия
экстремума. Достаточные условия
экстремума до первой производной.
кстремумы
функции. Необходимые условия
экстремума. Достаточные условия
экстремума до первой производной.
Т
 очка
х называется точкой необходимый
признак экстрем
очка
х называется точкой необходимый
признак экстрем max
ф-ции, если значение мума: ф-ия
а(x)
может иметь
max
ф-ции, если значение мума: ф-ия
а(x)
может иметьф-ции в этой точке max и min только в тех точках
- наименьшее в некоторой в которых f’(x)=0 или не сущ.
ее окрестности.
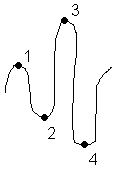
1- локальный max
2- локальный min
3- глобальный max
4- глобальный min
если tg>0, то f`(x)>0
если tg<0, то f`(x)<0
 (В
них можно построить
касательных).
(В
них можно построить
касательных).Достаточный признак: точка х0 является точкой экстремума, если ее производная в этой точке меняет знак:
- если с “+” на “-”, то х0- т. max
- если с “-” на “+”, то х0- т. min
-
Формула Тейлора с остаточным членом в форме Пеано.
Теорема. Пусть функция f(x) имеет в некоторой окрестности точки а производную порядка n+1. Пусть x – любое значение аргумента из этой окрестности. Тогда между точками a и x найдётся точка
 ,
что справедлива формула
,
что справедлива формула
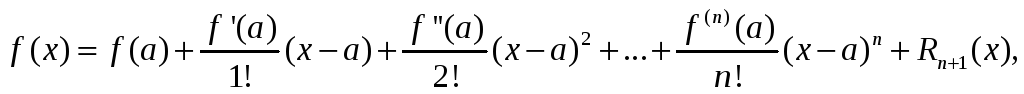 где
где

-
Представление функций ex, sinx, cosx, ln(1+x), (1+x) по формуле Тейлора. Применение формулы Тейлора для приближённых вычислений.
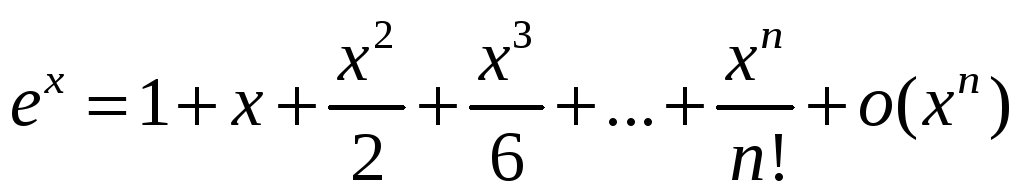
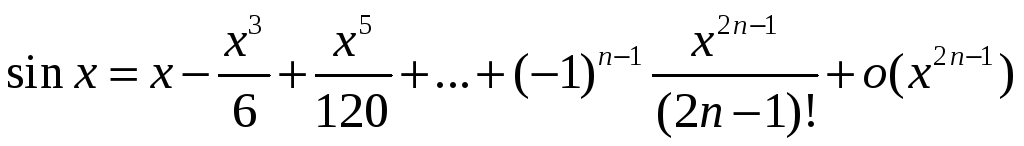
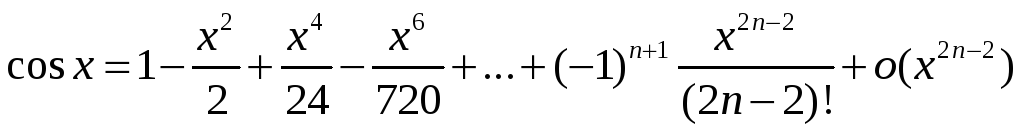
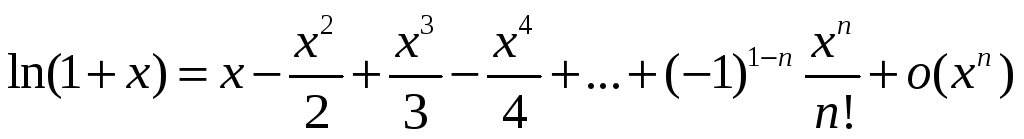
(1+х)ª =1+ах+(а(а-1)х²)/2+(а(а-1)(а-2)х³)/6+…+(а(а-1)…(а-n-2)* *хⁿ‾¹)/((n+1)!)+o(xⁿ‾¹)
Вычислим с точностью 10-3. Воспользуемся разложением 5 при
 =1/3
=1/3ФОРМУЛА –
 преобразуем сначала
преобразуем сначала
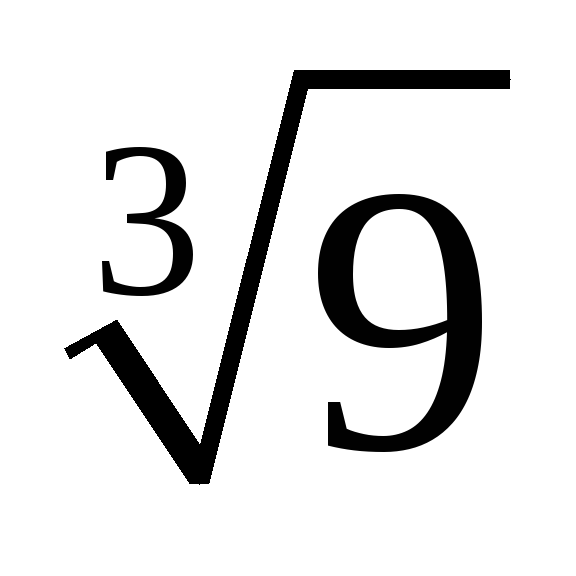 .
.
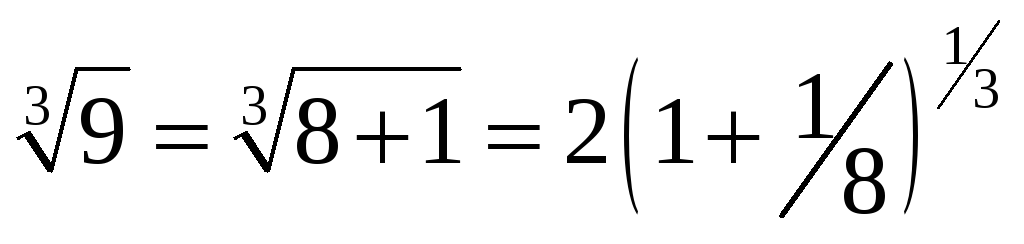
Применим ФОРМУЛУ, ограничась тремя членами
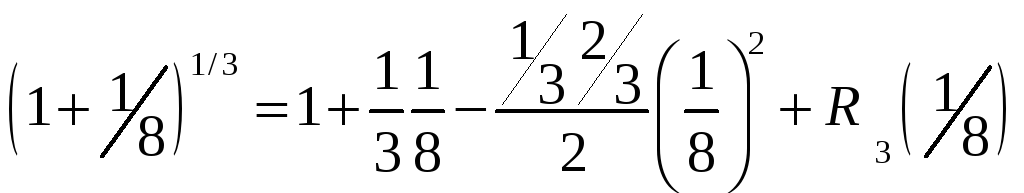 ;
;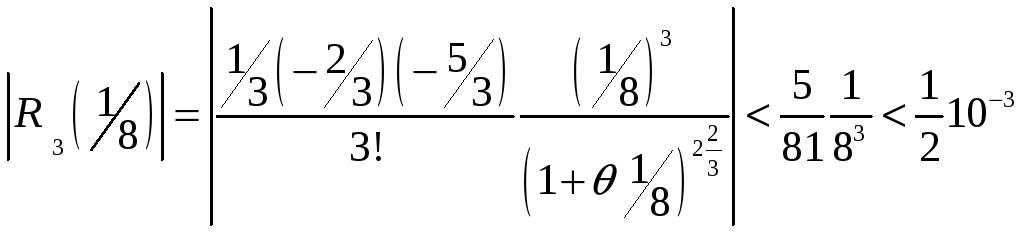 ,
здесь 0<
,
здесь 0< <1.
Таким образом с точностью 10-3
<1.
Таким образом с точностью 10-3
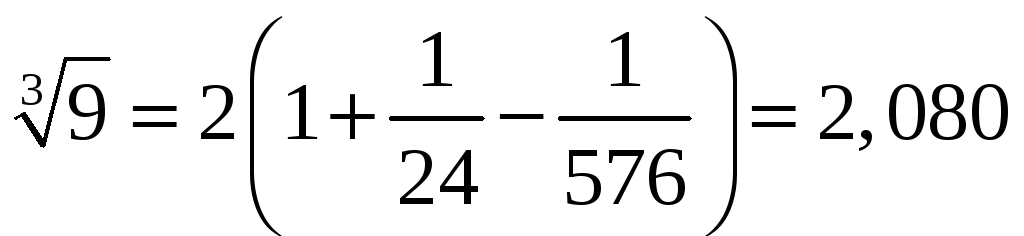
-
Направление выпуклости. Точки перегиба. Необходимое и достаточное условия. Исследование по высшей производной.
Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках. Линия называется вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.
Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.
Необходимый признак выпуклости и вогнутости: если линия на интервале выпуклая, то ее 2я производная <=0; если линия на интервале вогнутая, то ее f``(x)>=0
Достаточный признак: если f``(x) всюду в интервале “-”, то линия в интервале выпуклая; если f``(x)>0, то линия вогнутая.
Признаки точки перегиба: чтобы X0 была т. перегиба, <=> чтобы у`` в этой точке = 0 и меняла знак при переходе х через х0.
-
Исследование на экстремум с помощью производных высших порядков. Достаточное условие экстремума по второй производной.
Короче – если чётная производная (перед ней все нулевые), тогда как х2, а если нечётная производная (перед ней все нулевые), то как х3.
Теорема. Пусть функция f(x) имеет в стационарной точке x=c вторую производную. Тогда функция f(x) имеет в точке x=c локальный максимум, если f”(c)<0 и локальный минимум, если f”(c)>0.
Доказательство(для min). Так как f’(c)=0, то
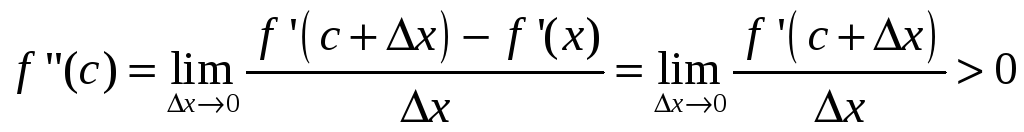 .
Так как
предельное значение больше нуля,
то
.
Так как
предельное значение больше нуля,
то
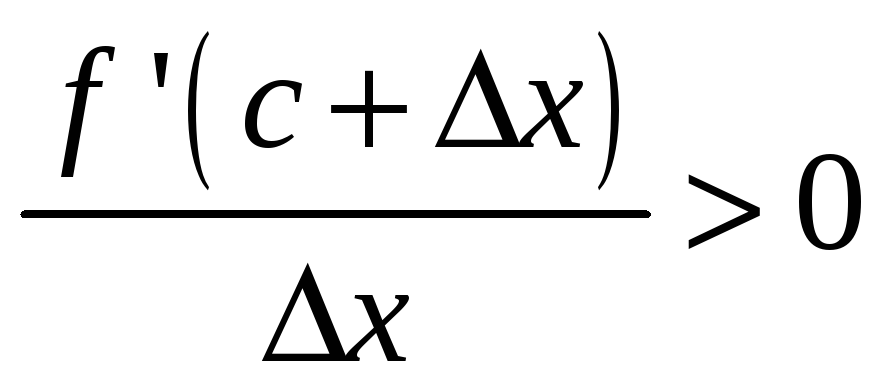 ,
при достаточно малых
,
при достаточно малых
 ,
т.е. для
,
т.е. для
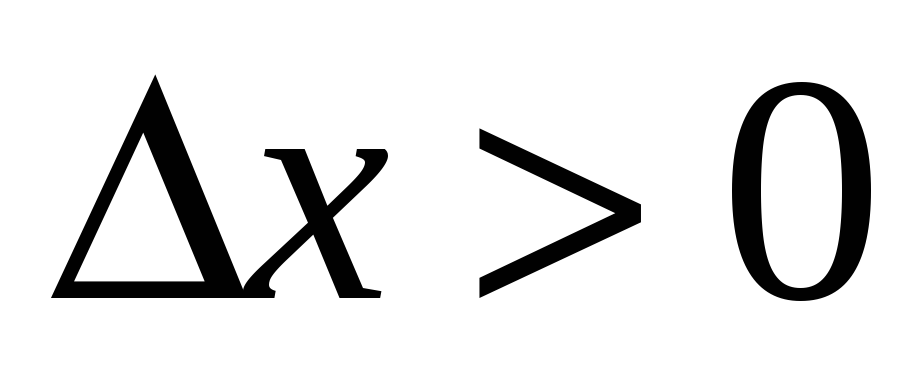 (справа от точки с),
а для
(справа от точки с),
а для
 (слева от с)
(слева от с)
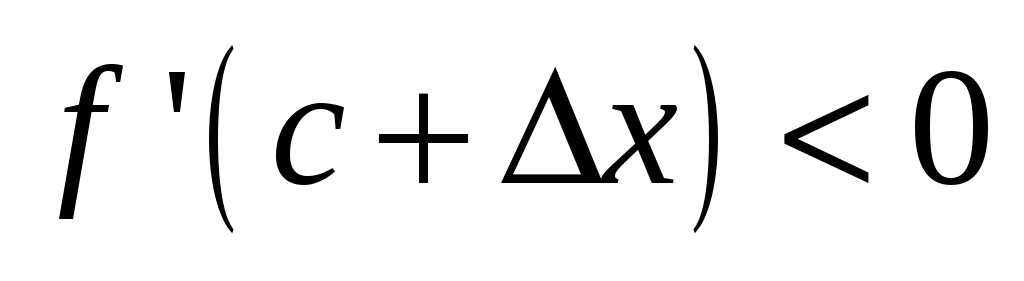 .
Получается (ну!..), чо точка x=c
– точка локального минимума.
.
Получается (ну!..), чо точка x=c
– точка локального минимума.-
параметрически заданные функции. Производная функции заданной параметрически. Касательная к кривой,заданной параметрически.
Пусть функции x = φ (t) и y = ψ(t) определены на некотором отрезке [α, β]. Переменную t будем называть параметром.
Если x = φ (t) взаимно однозначна на отрезке [α, β], то она имеет обратную функцию t(x) = φ − 1 (x). Подставляя ее в равенство y = ψ(t), видим, что переменная y является сложной функцией переменной x:
y = ψ(φ − 1 (x) ) ≡ f(x) .
В




 этом случае говорят, что функция y
= f(x)
задана
параметрически
уравнениями
этом случае говорят, что функция y
= f(x)
задана
параметрически
уравнениями
x = φ (t) (1)
 y
= ψ(t)
y
= ψ(t)
где t[a,b]
Производная первого порядка функции, заданной параметрически
Теорема 1. Пусть функция y = f(x) задана параметрически уравнениями (1), причем функции φ (t) и ψ(t) дифференцируемы в некоторой точке t0 О (α, β), и φ '(t0) ≠ 0.
Т
 огда
функция y
= f(x)
дифференцируема в точке x0
=
φ(t0),
причем
огда
функция y
= f(x)
дифференцируема в точке x0
=
φ(t0),
причем
f’(xo)= ψ’(t)
φ’(t) t=to
Доказательство.
В условиях теоремы функция j(t) имеет дифференцируемую обратную функцию t(x) = j − 1 (x), производная которой в точке x0 = j(t0) определяется формулой
t’(x)= 1/ φ’(t(x))
Д
 ифференцируя
f(x)
= ψ(t(x))
в точке x0
= j(t0)
как сложную функцию x,
при t
= t0
получаем
ифференцируя
f(x)
= ψ(t(x))
в точке x0
= j(t0)
как сложную функцию x,
при t
= t0
получаем
f’(Xo)= ψ’(t)*t’(x)= ψ’(t)
φ’(t) t=to
Касательная и нормаль к плоской кривой.
Пусть даны кривая y = f(x) и точка M (x1 ; y1) на ней. Требуется составить уравнения касательной. Как известно, угловой коэффициент k касательной к кривой y = f(x) в точке M (x1 ; y1) равен значению f '(x1) производной y' = f '(x) при x = x1/ Следовательно, уравнение касательной можно записать в виде уравнения прямой, проходящей через данную точку в данном направлении, т.е. в виде
y - y1 = f '(x1)(x - x1)

-
