Типовой расчет-Кратные интегралы-Вариант 15

7 _ 04 _15

Вычислить:

∫∫∫y

2

πxy

cos

dx dy dz;

V

2

x

= 0,

y = −1, y = x,

V

= 0, z = 2π2 .

z

Решение:

Т.к. подынтегральная фунуция не зависит от z, интегрирование нужно начать

по переменной z, при этом пределы интегрирования по z равны 0 и 2π2 . Если

затем интегрировать по y, то придется дважды интегрировать по частям,

поэтому проинтегрируем сначала по x, затем по y. Очевидно, что пределы

интегрирования по y будут -1 и 0, по x - y и 0.

2

πxy

0

2

0

πxy

2π2

2 0

2

2

πxy

0

∫∫∫y

cos

dx dy dz

= ∫

y

dy∫cos(

2

)dx ∫ dz = 2π

∫

y

dy

sin

2

=

V

2

−1

y

0

−1

π y

y

= −2π

2

0

2 2sin(π y2 / 2)

0

2

−cos

π y2

0

= 4

∫y

π y

dy = −4π ∫y sin(π y

/ 2)dy = −4

2

−1

−1

−1

7 _ 07 _15

Найти площадь фигуры, ограниченной данными линиями:

y2	−2 y + x2	= 0,
y2	−6 y + x2	= 0,

y = x 3 , x = 0.

Решение:

Два первых уравнения легко преобразовать к виду:

(y −1)2 + x2 =1 (y −3)2 + x2 = 9

Эти уравнения определяют окружности. Введем полярную систему координат:

x = r cosϕ

y = r sin ϕ

Окружность y2 −2 y + x2 = 0 имеет полярное уравнение

r2 sin2 ϕ −2r sinϕ + r2 cos2 ϕ = 0. Откуда r = 2sin ϕ. Аналогично

y2 −6 y + x2

= 0 r2 sin2 ϕ −6r sin ϕ + r2 cos2 ϕ = 0 r = 6sin ϕ.

Прямая y =

x

имеет полярное уравнение r sin ϕ = r cosϕ

.

3

3

Откуда tgϕ

= 1

3

ϕ =π

6

. Аналогично

x = 0 r cosϕ = 0 cosϕ = 0 ϕ =

π

2

Тогда площадь фигуры будет определяться по формуле:

π / 2

6 sin ϕ

π

/ 2

2

6 sin ϕ

π / 2

S = ∫∫dxdy = ∫

dϕ

∫ rdr =

∫

dϕ

r

= ∫ 16sin2 ϕdϕ =

D

π / 6

2 sin ϕ

π / 6

2

2 sin ϕ

π / 6

= (8ϕ + 4sin 2ϕ)

π 3

3

π

=16

+

≈11.84

π

8

6

6

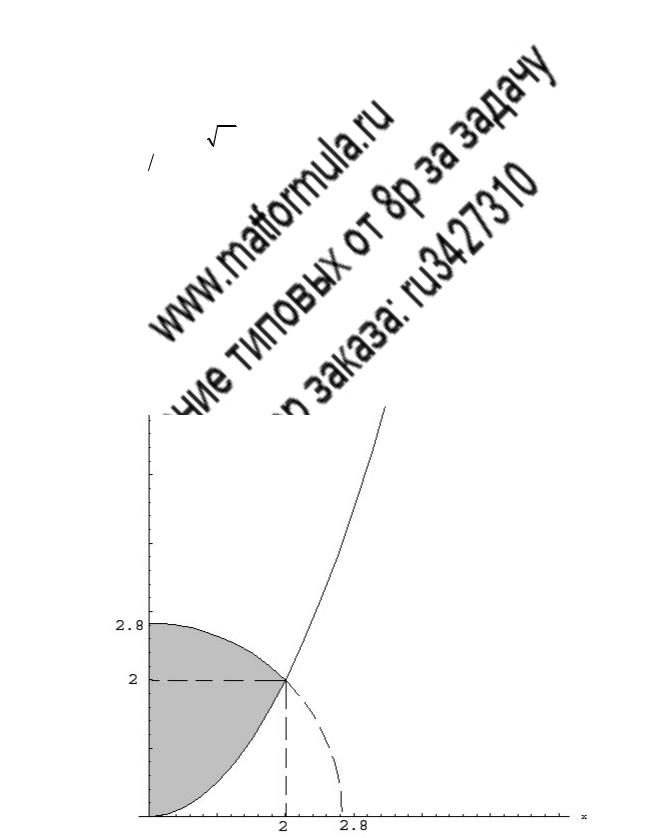
7 _10 _15 _1

Найти объем тела, заданного ограничивающими его поверхностями:

x2 + y2 = 8, x = 2 y, x = 0,
z = 30 y 11,		z = 0.
Решение:
					8−y	2		30 y /11				30						2	30			y2
				2										2		8−x				2			8−x2
V = ∫∫∫dx dy dz = ∫dy ∫							dx	∫	dz =				∫dx ∫					y dy =		∫			|2			dx =
												11							11			2
G				0	2 y			0						0			x2			0				x
																							2
																2
= 30	2		x	4			30			x	3		x	5	2
	8 − x2 −				dx =			8x −				−			|	=16
							22						20
22	∫0	4							3						0

7_10_15_2

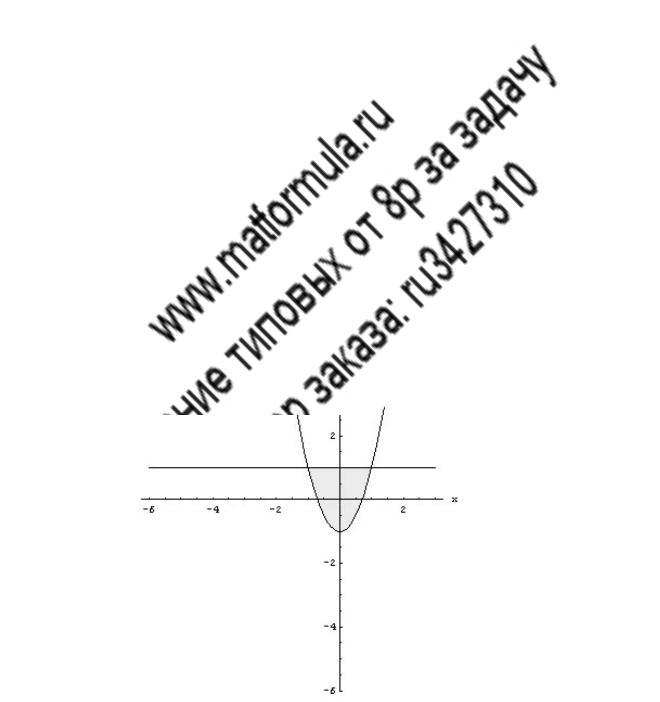
7 _12 _15 _1

Найтиобъем тела, заданного ограничивающими его поверхностями:

y = 2x2 −1,

y =1,

z = x2

−5 y2

−3,

z = x2

−5 y2 −6.

Решение:

1

1

x2 −5 y2 −3

1

1

1

(−2x2 + 2)dx =

V = ∫dx

∫

dy

∫

dz = ∫dx

∫

3dy = 3 ∫

−1

2 x2 −1

x2 −5 y2 −6

−1

2 x2 −1

−1

x

3

1

4

= 6 −

+ x

|

= 6

= 8

3

3

−1

7_12_15_2

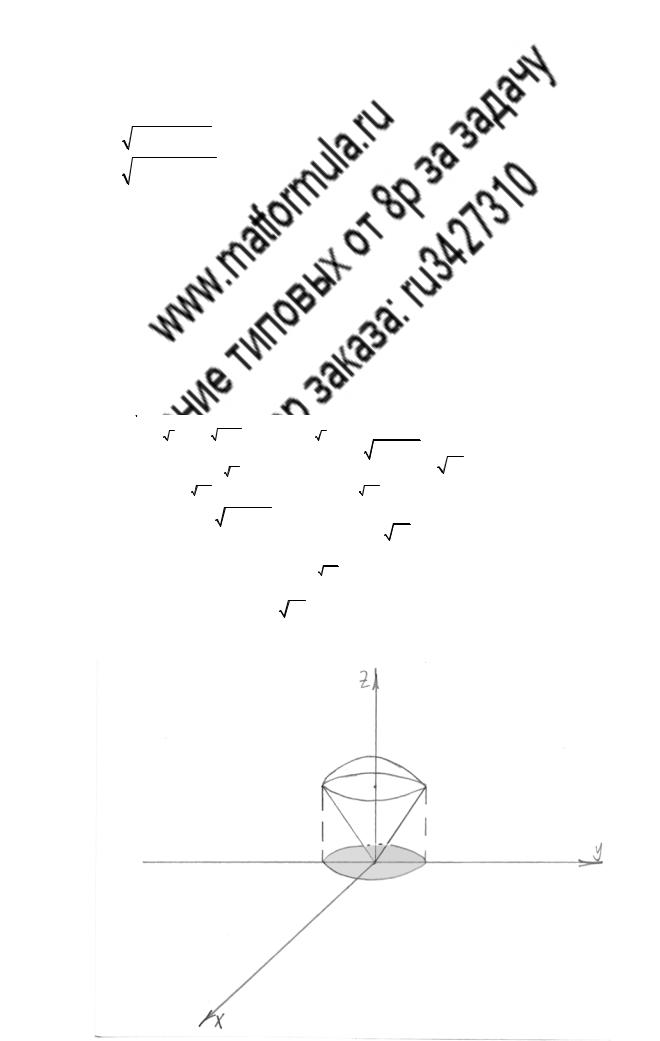
7 _13 _15

Найти объем тела, заданного ограничивающими его поверхностями: z = 36 − x2 − y2 ,

z = x2 + y2 63.

Решение:

Перейдем к цилиндрической системе координат:

x = r cosϕ

y = r sin ϕz = z

Найдем линию пересечения графиков функций:

							2				2			z																																3
z	= 36				− x				− y								= 36 −				(	x2 + y				2		)				z2			= 36 −				63z2				z	=
																																														4
			x	2	+ y			2									2			2					2									2			2			2									576
																																x			+ y			=	63z
z	=													x + y = 63z																														2			2
					63																																								+ y			=
																																										x							16
	2π				9 7 / 4						36−r2							2π			9 7 / 4													2				r
V =		∫dϕ				∫			r dr			∫	dz = ∫dϕ										∫	r					36			−r			−				dr		=
																																						63
		0				0					r /		63					0				0
2π										567																		567
						1			4									d (360r2 )−										4				r	2
= ∫dϕ					−					∫		36 −r2																∫						dr		=
						2																										63
0									0																			0
2π						1									3			r	3				567			2π
																						4
= ∫dϕ					−				(36 −r2 )2 −													|			=		∫63 dϕ =126π
						3												3 63
0																						0				0