Непрерыв-ть ф-ии в точке и на интерв. Св-ва непрер. Ф-ий. Точки разрыва и их классификация.

опр.: ф-ия y=f(x) непрерывна если левостор. предел f(a-0)равен правостор. f(a+0)

Т., в кот. наруш. услов. непрерыв-ти назыв. т. разрыва ф-ии.

опр.: y=f(x) непрерывна при x=a, если:

прав. нахожд. предела ф-ии в точке:

Все осн. элем. ф-ии непрер. во всех точках, где они определены.

Обозн-м: x-a = Δx, f(x)-f(a)=Δy; Δx-приращ. аргум. Δy-прир. ф-ии

опр.: ф-ия y=f(x) явл. непрер. на интерв. (x₁,x ₂) если она непрер. во всех т. этого интерв.

В т. x=a можно говор. о одностор. непрер-ти: левост. и правостор.

f(a-0)=f(a) – левостор. непрер-ть

f(a+0)=f(a) – правостор. непрер-ть

Точки разрыва - классиф. на т. 1 и 2 рода.

1 рода: 1) если  f(a-0) и f(a+0) конечные, но не равн.:f(a-0)f(a+0)

Т. x=a – т. скачка. - скачок

2) если  f(a-0) и f(a+0) конеч., и они равны, но не равн. f(a)

f(a-0)=f(a+0)f(a). Т. x=a – т. устраним. разрыва. Подразум., что разр. можно устран., определить ф-ию в т. x=a

2 рода: либо f(a-0), либо f(a+0), либо оба вместе, или не сущ., илит равны , тогда x=a – т. разр. 2 рода.

Св-ва ф-ий непрерыв. в т.: 1) если y=f₁(x) и y=f₂(x) непрер. при x=a, то на осн. теор. о пред. и опр. непр-ти в т. непрер-ми. будут также: f₁(x)f₂(x); f₁(x)f₂(x); f₁(x)/f₂(x), если f₂(x)0

2) если y=f((x)) в т. x=a. =(x) – непрер. при х=а

(а)=₀; f() – непрер. по . f(₀)=f₀. Тогда исход. ф-ия непрер. при х=а

Св-ва ф-ий непрерыв. на замк. отр.[a;b]:

1) если y=f(x) непрер. x[a,b] при f(a)=A>0, f(b)=B<0, то  x=c(a,b) такое, что f(c)=0.

замеч.: если услов. непрер. наруш., то необяз. сущ. с такое, что f(c)=0

2) если y=f(x) непрер. x[a,b] причем y[A,B], то  y=C[A,B]  x=c[a,b] такое, что f(c)=C

3) теор. Вейерштрасса (1): если y=f(x) определ. и непрер. на [a,b], то она огранич. снизу и сверхуб т.е. mf(x)M

4) теор. Вейерштрасса (2): если y=f(x) опред. и непрер. на [a,b], то она достигает своего наиб. и наим.

1 замеч. пред. и след. из него.

- 1 зам. пред.

f(x)=sinx/x при х=0 не сущ.

f(x)=f(x) – четн. Поэтому рассмотрим:

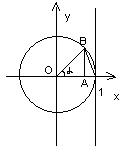
; Чтобы доказать рассмотрим:

S_ΔOAB<S_{сект. ОАВ}<S_ΔOAC

1/2sinα<1/2α<1/2tgα

Поделим на sinα:

1<α/sinα<1/cosα

1>sinα/α>cosα

На осн. теор. о пред. промеж. ф-ии сдел. заключ., что:

т.к. lim1=1;

СЛЕДСТВИЯ:

1) осн. на теор. о пред. отнош.

2) k0, тогда: при х→0 y→0

3) т.к.

4)

5) т.к. если ввести обозн. arcsinx=y, то при x→0 y→0

6)

7) Вообще: если

Переход к пред. в степени

Осн. Эл. ф-ии непрер. там, где они опред.

y=x^α y=a^x a>0, a1

Покажем, что limx^y=a^b x>0 limx=a limy=и

На осн. логар. тожд.: x=e^lnx

limx^y=lime^ylnx=lime^blna=(e^lna)^b=a^b

Обратим вним. что blna=0

1) a=1 b= «1^»

2) а=0 b=0 «0⁰»

3) a= b=0 «⁰» Всего 7 неопред.: 0/0, /, 0, -, 0⁰, 1^, ⁰

Теор.: 2 зам. пред.: е-иррац. число=2,7…

Док-во: рассм. пред. послед-ти:

U_n=(1+1/n)ⁿ U₁=2 U₂=9/4 U₃=64/27 …

Эта посл-ть возраст. и огранич. сверху, ее пред явл. число е

Обратим. вним. на неопред.

Дан. зам. пред. част. использ. в др. виде:

К эт. ф-ле можно придти из теор., если сдел. зам. перем.

1/x=y

при x→ y→0

замеч.: если (х)→0 - 2 замеч. пред.