Глава Обыкновенные Дифференциальные Уравнения (ду) §1 Дифференциальные уравнения : основные понятия, примеры.

Пусть n раз дифференцируемая функция k переменных (в D_f определены n функций f^(m)(x), m=0,1,..,n и (n-1) из них непрерывны).

Определение 1. Дифференциальным уравнением (ДУ) порядка “n” называется уравнение ;, связывающее аргумент х, функциюf и ее производные функции , порядок старшей из которых равен “n”, при этом ДУ относительно функции одной переменной (к=1) называют «обыкновенным ДУ», а ДУ относительно функции нескольких переменных (k>1) и ее частных производных называют «ДУ в частных производных» .

Например, (1) xy^//+2y^/+xy=x; (2)y”=x - обыкновенные ДУ второго порядка.

(3) - система двух дифференциальных уравнений в частных производных первого порядка относительно дифференцируемой функции U(x,y) двух переменных.

Определение 2. Дифференцируемая функция f, подстановка которой обращает ДУ в тождество в области , называется решением ДУ. График решения ОДУ y=f(x) называется интегральной кривой ДУ. Нахождение множества решений ДУ называют интегрированием ДУ.

Например, функция y₁(x)=1+sin(x)/x является решением ДУ (1), так как

.

Проверьте, что :

• функция y₂(x)=1+cos(x)/x так же является решением ДУ (1);

• множество функций 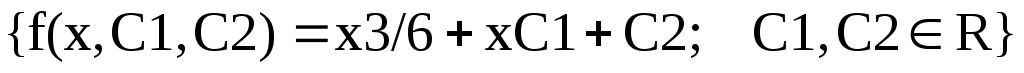включает все решения ДУ(2);

• функция U(x,y) = x²+xe^xy +1 является решением системы ДУ(3), удовлетворяющим начальному условию U(1;0)=3.

В дальнейшем будут рассматриваться только обыкновенные ДУ.

Поскольку есть Уравнение, возникают вопросы: 1)существует ли решение?; 2)единственно ли оно?; 3) как найти множество решений?

Рассмотрим несколько примеров.

1) Известно, что ДУ первого порядка y^/(x)=f(x): (а) имеет решение для любой кусочно непрерывной (интегрируемой) функции f(x) и это решение y=F(x) называется первообразной для функции f; (б) существует бесчисленное множество решений и (в) это множество называется неопределенным интегралом , содержит одну аддитивную произвольную константу и соответствующие интегральные кривые представляют семейство параллельных гладких линий y=F(x)+C, причем через каждую точку проходит единственная интегральная криваяy=F(x)+(y₀-F(x₀).

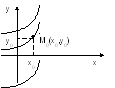
Например,

2) Найдем множество решений ДУ 2 порядка

Это множество содержит две произвольные константы, фиксированные значения которых С₁=С₀, С₂=D₀ определяют единственную интегральную кривую y(x,C₀,D₀)=x³/6+C₀x+D₀, проходящую через точку M₀(x₀,y₀); y₀=x₀²/6+C ₀x₀+D₀ , тангенс угла наклона которой в этой точке равен tg(α₀)=y’(x₀,C₀)=x₀²/6+C₀^.

Определение 3. Решение f(x) ДУ порядка “n”, удовлетворяющее “n” начальным условиям , называется решением задачи Коши с начальными условиями: 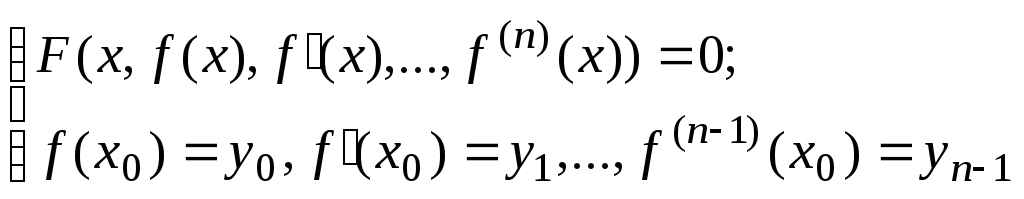Например, функцияf(x)=x²/2+1 является решением задачи Коши

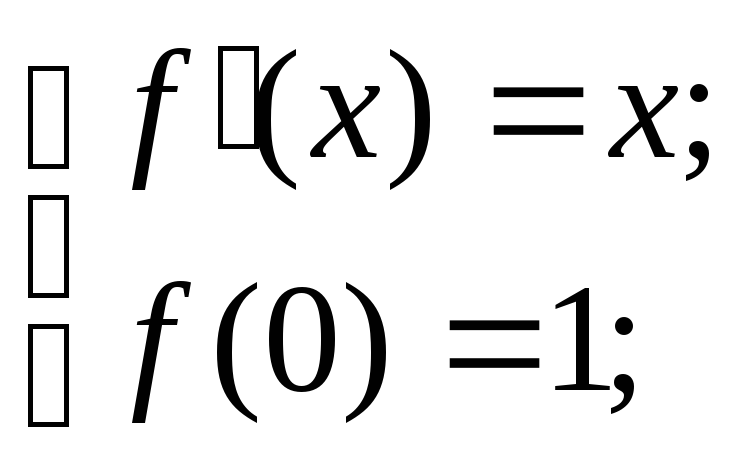
Найдем решение задачи Коши для ДУ 2 порядка :

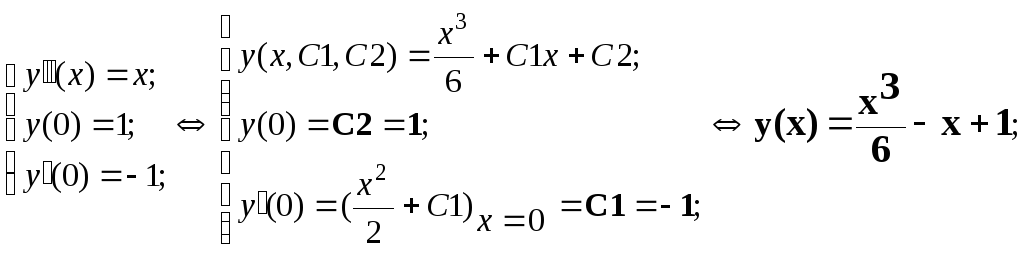
ЭКЗ. Для ДУ 2 порядка найти: 1)множество решений; 2)решение задачи Коши с начальными условиями :

§2 Ду 1 порядка с разделяющимися переменными

Рассмотрим ОДУ 1 порядка y’(x)=f(x,y) и точку (x₀,y₀) на плоскости.

Ответ на вопрос существования его решения дает следующая

Теорема (существования и единственности решения задачи Коши ).

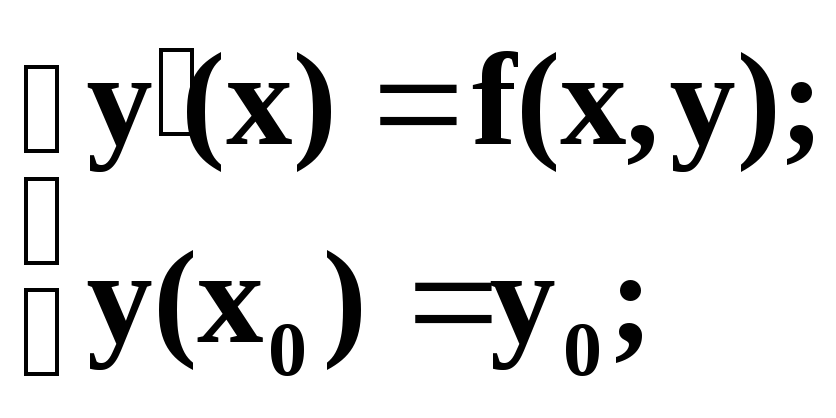«Если в области функции двух переменных непрерывны и точка, задача Коши имеет в областиD единственное решение – дифференцируемую функцию у(х,х₀,у₀)».

Замечания.

1) По теореме через каждую точку области D проходит одна интегральная кривая y=y(x,x₀ ,y₀).

2) Если область определения функции y(x,x₀ ,y₀) является объединением нескольких интервалов, решением задачи Коши она является лишь в той ее части, в которой находится начальная точка (х₀,у₀) и в которой эта функция непрерывна и дифференцируема.

Определение. Дифференциальным уравнением с разделяющимися переменными (ДУРП) называется ДУ 1 порядка

Если функция p(x) непрерывна на промежутке (a;b), а функция g(y) непрерывно дифференцируема на (c;d), через каждую точку прямоугольной области проходит единственная интегральная кривая этого ДУ.

Рассмотрим алгоритм решения ДУРП на примере: (1)

1. 

Так как условия теоремы выполнены , задача Коши слюбыми начальными условиями имеет единственное решение.

2) Очевидно, что функция-константа удовлетворяет ДУ: , так что y(x)≡0 – частное решение ДУ. (2)

2. Домножим ДУ на dx 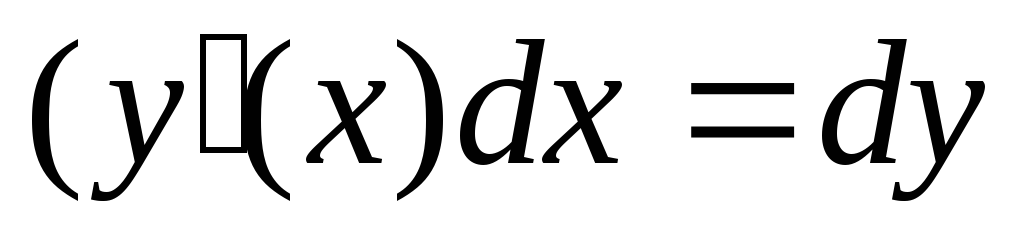), разделим его на у² и получим ДУ с разделенными переменными:

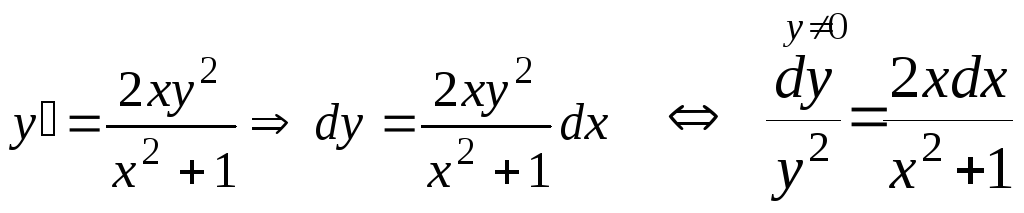(2)

После интегрирования получим уравнение

[Ф(x,y(x),С)=0] (3)

которое при всех допустимых значениях константы С определяет множество решений ДУ и называется “общим интегралом” ДУ.

Если из общего интеграла удается записать явное выражение функции

Ф(x,y(x),С)=0 ,

его называют «общим решением» ДУ.

Таким образом, множество решений ДУ(1)

(4)

3. Решение задачи Коши следует искать в множестве (4). Например, для начального условия y(0)=1 найдем его из общего решения:

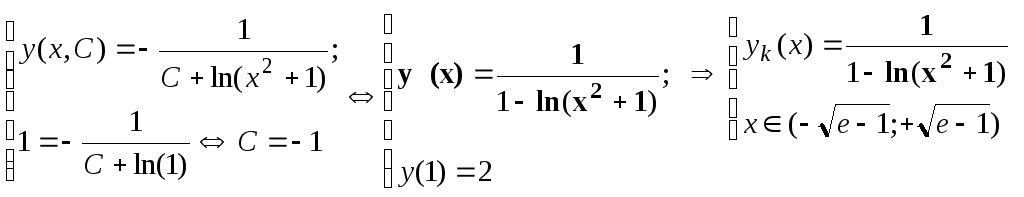
На рис.1 приведены графики y(x)≡0;

_{Обратите внимание :}

_{1)ДУ определено на всей плоскости; 2) функция у(x) является решением ДУ на R/{t1,t2}, но 3) решением задачи Коши с начальным условием y(0)=1 функция у(x) (как дифференцируемая функция) является лишь на (t1;t2). 4) аналогично, функция у(x) является решением задачи Коши с начальным условием y(- 2)=1/(1-ln(5)) на (-∞;t1), а с условием y(2)= 1/(1-ln(5)) – на (t2;+ ∞); решением же задачи Коши с начальным условием y(2)=0 является функция y(x)≡0; x€R.}

Замечания.

1) В общем случае ДУРП имеет вид

.

Алгоритм его решения:

1. Находятся корни функций 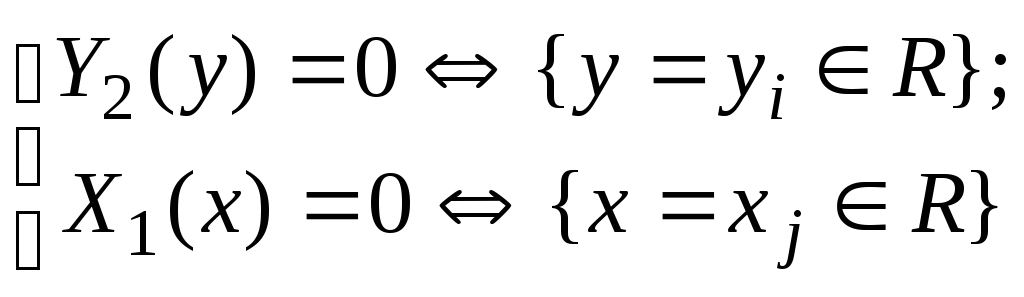и соответствующие «частные решения» ДУ - функции-константы: .

2. Записывается ДУ с разделенными переменными:

,

после интегрирования которого находится «общий интеграл» ДУ:

2) С помощью подходящих преобразований к ДУРП приводятся некоторые типы дифференциальных уравнений. Способы таких преобразований можно найти в математических справочниках; в «Сборнике задач по математике; ч.2; А.В. Ефимов,Б.П.Демидович» эти способы иллюстрируются примерами.

Например,

1) ДУ вида y’=f(ax+by)  dy=f(ax+by)dx приводятся к ДУРП, если ввести «новую» функцию

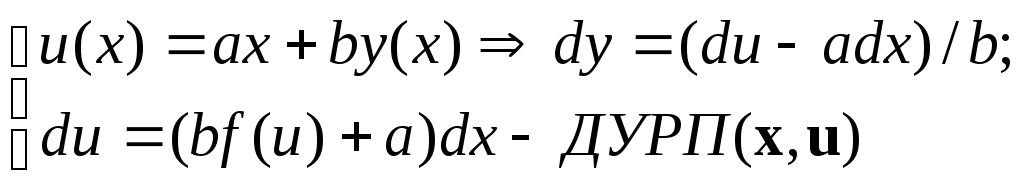
2)C помощью подстановки y(x)=xU(x) к ДУРП сводится “Однородное ДУ” :

Например,