Контрольная работа 1,2 по ВМ для зачников вариант 4

Г
	КОНТРОЛЬНАЯ РАБОТА ПО ВЫСШЕЙ МАТЕМАТИКЕ.
о
м	т		МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ.
аг
Перед выполнением контрольной работы студент должен изучить
		вы
соответствующие разделы курса по рекомендуемым источникам. При затруднении в
а
освоении теоретического или практического материала он может получить
зин
консультацию на кафедре высшей математики.
		е
Каждая ко трольная работа должна быть выполнена в отдельной тетради, на
http://www
обложке которой студенту следует разборчиво написать свою фамилию, инициалы и
	ракон
адрес, шифр, номер контрольн й работы, название дисциплины и дату отправки

работы в университет.

Задачи для контрольной рабо ы следует выбирать в соответствии с номером,
б		т
который совпадает с последней циф ой учебного шифра студента. Условие задачи
		р
должно быть полностьюопереписано перед решением.
.	удент		од лжен исправить отмеченные рецензентом ошибки и
В зачтенной работе с

	учесть	все рекомендацииna4и советы. Ес и же работа не зачтена, то ее выполняют еще
		-л
	раз и отправляют на повторную рецензию. Зачтенные контрольные работы
			ьны
	предъявляются студентом при сдаче зачета или экзамена.
		.
		na4
		by/	ЛИТЕРАТУРА.
	1.Беклемишев, Д.В. Курс аналитической г ом трии и линейной алгебры. 4-е изд. /
		.		е
	Д.В. Беклемишев. - М.: Наука, 1980
		by
	2.Бугров. Н.С. Высшая математика. Дифференциальное и интегральное
		-			, 1980.
	исчисления / Н.С. Бугров, С.М. Никольский. - М.: Н
				ука
	3.Бугров, Н.С. Дифференциальные уравнения. Кр тные интегралы. Ряды.
		уч		бот
	Функции комплексного переменного / Н.С. Бугров, С.М. Никольский. - М.: Наука,
	1981.
	4.Данко. П.Е. Высшая математика в упражнениях и задачах. Ч. I, II / П.Е. Данко,
		ш			ы
	А.Г. Попов, Т.Я. Кожевникова. - М.: Высш. шк., 1980.
	5.Жевняк, М.Р. Высшая математика: В 4 ч. / М.Р. Жевняк. А.А. Карпук:
			ие
	Ч.1. - Минск: Выш. шк., 1992; Ч.2 - М нск: Выш. шк., 1993: Ч.3, 4. - Минск:
	Обозрение, 1997.
	6.Клетеник. Д.В. Сборник задач по аналитическойц				геометрии /Д.В. Клетеник. -
	М.: Наука, 1965 -1980.			е	ого. Операционное исчисление.
	7.Краснов. M.JI. Функции комплексного п р м
				н
	Теория устойчивости (задачи и упражнения) / МЛ. Краснов. А.И. Киселев. Г.И.
	Макаренко. - М.: Наука, 1971.			ы
	8.Пискунов, Н.С. Дифференциальное и интегральное счисление для втузов. В 2
	т. / Н.С. Пискунов. - М.: Наука. 1985.			и
	9.Задачи и упражнения по математическому анализу для втузов под ред. Б.П.
	Демидовича. - М.: Наука, 1964-1978.				к

10.Высшая математика: Методические указания для студ. р диотех. спец. заоч.
формы обуч. В 2 ч. 4.1	/ Сост. О.Ф. Борисенко, Л.А. Конюхач. Н.И. Кобринец. - Минск:
БГУИР, 2001. - 56 с.
11.Высшая математика: Методические указания для студ. радиотех. спец. заоч.
формы обуч. В 2 ч. 4.2	/ Сост. О.Ф.Борисенко, Л.А.Конюх, Н.Иест. Кобринец. - Минск:
БГУИР, 2001. - 48 с.	во

Г

Даны четыре вектора

a (а1, а2, а3), b (b1, b2, b3),

Задача 04.

о

d (d1, d2, d3) в некотором базисе. Показать, что векторы a , b ,

c (c1

, c2

, c3) и

м

тов

c образуют базис, и найти координаты вектора d в этом базисе.

а

b (0,2,0),

c (5,7,9),

d (0,4,16).

a (1,3,5),

газ

является любая

Решение: Как известно, базисом в пространстве R

3

упорядоченнаяысистема из трёх линейно независимых векторов. Покажем,

что векторы

a

, b

и c линейно независимы, т.е. выполняется равенство:

и

е

α1a +α

2b +α3c = 0

http://www

нран

α3

одновременно равны нулю.

при условиик, что все числа α1 , α2 ,

о

b , c , получаем:

Подставляя в это раве

ство координаты векторов a ,

α1 (е1 + 3е2

+ 5е3) + α2 (2е2) + α3 (5е1 + 7е2 + 9е3) = 0

т

или

бо

р

(α1

+ 5α3 ) ∙ е1

+ (3α1 + α2 + 7α3 ) ∙ е2 +(5α1 + 9α3 ) ∙ е3 = 0

Для того, ч

бы вект

, разложенный по базису е1, е2, е3 был равен

.

т

нулевому вектору, его координаты должны равняться нулю, т.е.

na4

α1 +5α3

= 0

3

-

ль1

2

3α + 2α + 7α = 0

.

= 0

5α1 +9α

3

Получим однородную системунытрех линейных уравнений с тремя

na4

неизвестными

α1 , α2

, α3 . Такая система имеет нулевое решение (α1 =0, α2 =0,

by/

.

е

α3 =0), если её определитель не равен нулю.

4-5 2

by

р

Поскольку

лу

,

або

3

0

1

= −27

≠ 0

−1

4

2

то векторы a ,

b ,

c линейно независимы. След ва ельно, они образуют

ч

т

базис и вектор d является линейной комбинацией векторов a , b , c : d =

β1а+ β2b + β3c . Числа

β1 ,

β2

ш

ы

, β3

будут координатами вектора d в базисе a , b ,

c . Найдем их.

и

Воспользовавшись разложением a , b , c ,

d в базисе е1, е2, е3, имеем:

12 е2 - 6 е3

= β1 ( е1 + 3 е2

+ 5

3) +

β2

(2 е2) + β3 (5 е1 + 7 е2 + 9 е3)

це

Или

12 е2 - 6 е3 = ( β1

+ 5 β3 ) е1 + (3 β1 + 2 β2 + 7 β3 ) е2 + (5 β1 + 9 β3 ) е3.

Из равенства векторов следует рав

ство их координат, поэтому

получаем систему:

н

ы

β1 +5β3

= 0

+ 2β

2 + 7β3

= 4

3β1

и

5β1 +9β3 =16

Решая её по формулам Крамера βi

= ∆i

∆

, i =1,2,3

, находим:

0

0

5

5

0

5

5

0

0

ка

ч

∆1 =

4

2

7

= −160 ,

∆2

=

3

4

7

= 64 ,

∆

3

=

3

2

4

=

32 .

16

0

9

5

16

9

5

0

16

е

Следовательно, β1 =

−160

−

32

= 5, β2 = 64

−32

= −2

, β3 = 32

−

32

= −1, т.е.

координаты вектора d в этом базисе: d =(1,-1,0).

ств

Задача 14.

Даны координаты вершин пирамиды A1A2Aо3A4. Найти:

Г

А2;

1) длину ребра А1

2) оуг л между ребрами А1А2 и А1А4;

м

3) уг л между ребром А1А4 и гранью А1А2А3;

тов

а4) площадь грани

А1А2А3;

г5) объём пирамиды;

а6) ур внения прямой А1А2;

ы

А2А3;

7)зур внение плоскости А1

8)уравнения

в соты, опущенной из вершины А4

на грань А1А2А3.

Сделать чертёж.

http://www

нраРешение:

А4(3,6,7).

А1(2,4,3),

Аек2(7,6,3), А3(4,9,3),

о

1)

найдёмбкоординта ы и длину вектораА1 А2 :

А1 А2

= (5,2,0),

оА1 А2 = 25р+ 4 =

29

.

о

А1А2 и А1А4.

2) найдемтуг л между ребрами

[A1 A2 ,

A1 A ]

ль

A1 A2

A1 A

sinϕna4=

-

ны

.координаты и дли у вектора А А :

Для этого найдёмna4

1

4

А1 А4 = (1,2,4),

А1

А4

=

=

21

1+ 4 +16

by/

Векторное произведение векторов.:

еА1 А2 и А1 А4 :

i

j

k

by

р

[A1 A2 ,

A1 A4 ]

-

2)i + (0

(5 2 − 2 1)k = 8i − 20 j +

8k =

=

5

2

528

0

= (2 4 −0

1−5 4) j +

1

2

4

лу

або

528

sinϕ =

≈

0,9311; ϕ ≈ 68,6°

29

21

ч

т

ш

ы

3) угол между ребром А1

А4

гранью А1А2

А3

и

найдем каноническое уравнение р бра А1А4

х− x4

=

y − y4

=

z

− z4

,

е

l

m

p

це

х−3

y −6

z −7

2,

4)

s = (l,

m,

p) = (1,

=

=

– каноническое уравн ие ребра А1А4

1

2

4

н

Найдем уравнение плоскости, проходящей через точки

А1(2,4,3),

А2(7,6,3),

А3(4,9,3):

ы

x − x1

y − y1

z − z1

и

x2 − x1

y2 − y1

z

2 − z1

= 0

ка

x3 − x1

y3 − y1

z3 − z1

x − 2 y − 4 z −3

x − 2 y − 4 z −3

7 − 2 6 − 4 3 −3

=

5

2

0

= 0

ч

4 − 2 9 − 4 3 −3

2

5

0

е

ств

(x − 2)(0 −0) + ( y − 4)(0 −0) + (z −3)(25 − 4) = 0

уравнение плоскости, проходящей через точки А1, А2, А3:

z −3 = 0

о

Г

и гранью А1А2А3

Синус угла между ребром А1А4

о

Al + Bm +Cp

мsin

γ =

A2

+ B2

+C 2 m2

+l 2

+ p2

а

тов2 2 2

2

2

2

sin γ =

0 1+ 0 2 +1

4

=

4

≈ 0,8729

газ

+ 0 +1 1 + 2 + 4

21

0

γ ≈ 60,7°

ы

и

4)

площадь грани А1А2А3;

http://www

н

Грань

А1

А2

Аек3 – это треугольник, площадь которого равна ½ площади

параллелог амма,оп стр енного на векторах А1 А2 и А1 А3

А1раА2 = (5,2,0),

А1А3

бнт

= (2,5,0),

р

о

Векторн е пр изведение векторов:

.

т

о

5

2

AB,

AC

2

0

,

−

5

0

,

=

na4

-5 0

ль

2 0

2

5

AB,

AC

= (0,

0,

21)

.

ны

Находим площадь треугольника А1

А2А3:

na4

SA A A

= 1

21 =10,5

02

+

02 +

212

=

by/

. е

1

2

3

2

2

by

р

5) объём пирамиды-;

V =

1

(A A

A A A A )

лу

або

6

1

2

1

3

1

4

А1 А2 = (5,2,0),

ч

т

А1А3

= (2,5,0),

ш

ы

А1 А4 = (1,2,4),

и

Смешанное произведение

ев кторовA1 A2 , A1 A3 , A1 A4 :

(A1 A2 A1 A3 A1 A4 )=

5

2

0

це

2

5

0

=100 −16 =

84

1

2

4

н

объём пирамиды V =

1

84 =14

ы

6

6) уравнения прямой А1А2;

а). Как пересечение двух плоскостей А1А2А3 и А1А2А4:

и

уравнение плоскости, проходящей через точки А1, А2, А3:

z +3 = 0

к

Найдем уравнение плоскости, проходящей через точаи

А1(2,4,3),

А2(7,6,3),

А4(3,6,7):

ч

x − x1

y − y1

z − z1

е

x2 − x1

y2 − y1

z2 − z1

= 0

ств

x3 − x1

y3 − y1

z3 − z1

о

Г

z −3

x − 2 y − 4 z −3

x − 2

y

− 4

м

7 −о2 6 − 4 3 −3

=

5

2

0

= 0

3 −

2 6 − 4 7 −3

1

2

4

а

(x − 2)(8 −0) + ( y − 4)(0 − 20) + (z −3)(10 − 2) = 0

газ

ур внениетовплоскости, проходящей через точки А1, А2, А4:

2x −5y + 2z +10 = 0

ы

Общ е уравнения прямой А1А2:

и

ек

z −3 = 0

http://www

н

0

2x −

5y

+

2z

+10 =

о

ра

б). каноническое урав е ие прямой А1А2:

l

=

m

=

p

нт,

х− x2

y

− y2

z

− z2

.

бото

s = (l,

m,

p) = (5,

2,

р

0)

х−7

=

y −6

= z −3 – каноническ е уравнение ребра А1А2

5

2

0

-

ль

na4

с). параметрическое уравнение прямой А1А2:

x = x0

+lt

.

ны

na4

y = y0

+ mt,

t R

by/

. е

+ pt

z = z0

by

р

x = 2 +5t

-

t R

або

y = 4 + 2t,

лу

x = 2 +5t

z = 3 + 0t

ч

т

y = 4 + 2t,

t R

ш

ы

z = 3

7) уравнение плоскостииА1А2А3;

А1(2,4,3),

А2(7,6,3),

е

А3(4,9,3):

це

x − x1

y − y1

z − z1

x2 − x1

y2 − y1

z

2 − z1

= 0

н

x3 − x1

y3 − y1

z3 − z1

x − 2 y − 4 z −3

x − 2 y − 4 z −3

ы

7 − 2 6 − 4 3 −3

=

5

2

0

= 0

и

4 − 2 9 − 4 3 −3

2

5

0

:

уравнение плоскости, проходящей через точки А1, А2

, А3

z −3 = 0

ка

ч

8) уравнения высоты, опущенной из вершины Ае4 на грань А1

А2

А3.

уравнение плоскости, проходящей через точки А1, А2

, А3

:

z −3 = 0

ств

Нормальный вектор данной плоскости

о

n = (0,

0,

1)

Г
Уравнение высоты А4Н, опущенной из т. А4(3,6,7) на плоскость А1А2А3,
имеетовид:
м	= y −6	= z −7
х−3
а0	0	1
гНайдем координаты т.Н:
	тов								x = 3
а
	ы									6
Решзя параметрическое уравнение прямой А4Н y =
ие										7 +1t
									z =
http://www						А2	А3: z −3 = 0 , имеем: t = −4 , отсюда координаты
и уравне ие плос ости А1
т.Н:		к
	x = 3		о
	ра				нт
	y = 6
	z = 3				р
	.
							y
		бото
na4				-
		.				ль
				na4
	by/						ны
						.		A3
								е
					by				р
					-
					лу			Н	або	A2
					ч
									т
						шA1			ы
					A4		и
							е
								це		x
									н
									ы
									и
z									ка
									ч
										е
										ств
										о

Г

Задача 24. Вычислить координаты центра окружности, описанной

о

м

около реугольника с вершинами A(-1,1), B(2,-1), C(4,0).

а

тов

Решение:

Центр описанной окружности, описанной около треугольника, является

ы

газточкой пересечения серединных перпендикуляров к сторонам треугольника.

ие

Найдем уравн ния прямых, на которых лежат стороны треугольника и их

http://www

нра

угловые коэффициенты:

АВ:

x +1

y −1

оx +1 y −1

; kAB = −2

=

=

− 2(x +1) = 3( y −1) 2x +3y −1 = 0

3

2 +1

−1−1

3

− 2

нт

.бот

о

x − 2

y +1

x − 2

y +1

ВС:

=

=р1(x − 2) = 2( y +1) x − 2y − 4 = 0 ;

kAB

= 1

2

4 − 2

0 +1

2

1

na4x +1 y −1

x +1

ль

y −1

АС:

=

-=

−1(x +1) = 5( y −1) x +5y − 4 = 0 ;

kAC

= − 1

5

4 +1

0 −1

5

−1

.

ны

Координаты середин сторон:

na4

−1+ 2

;

1−1

;

D(0,5; 0)

D

by/

. е

2

2

2 + 4

;

−1+ 0

;

Е(3;

by

р

Е

−0,5)

2

2

-

або

−1+ 4

1+ 0

лу

F

2

;

2

;

F(1,5;

0,5)

ч

Угловые коэффициенты перпендикулярных прямтх имеют обратную

пропорциональность:

k1

ш1

ы

= −

k

2

kDO

=

3

;

kEO = −2 ; kFO = 5

и

2

е

Уравнения серединных высот:

y − y0 = k(x − x0 )

DO: y −0 =

3 (x −0,5) 2y −3x +1,5 = 0це

2

н

EO: y + 0,5 = −2(x −3) y − 2x + 6,5 = 0

ы

FO: y −0,5 = 5(x −1,5) y −5x + 7 = 0

2y −3x +1,5 = 0			125	≈1,79
	0	x =	70
y + 2x −5,5 =			135
				≈1,93
y −5x + 7 = 0		y =	70

и

ка ч е ств о

Г

о

y

м

а

тов

ы

газ

ие

http://www

н

к

о

ра

нт

р

.бот

о

na4

-

ль

А

.

F

na4

by/

ны

. е

E

С

x

byD

р

-

лу

абоВ

ч

т

ш

ы

и

е

це

н

ы

и

ка

ч

е

ств

о

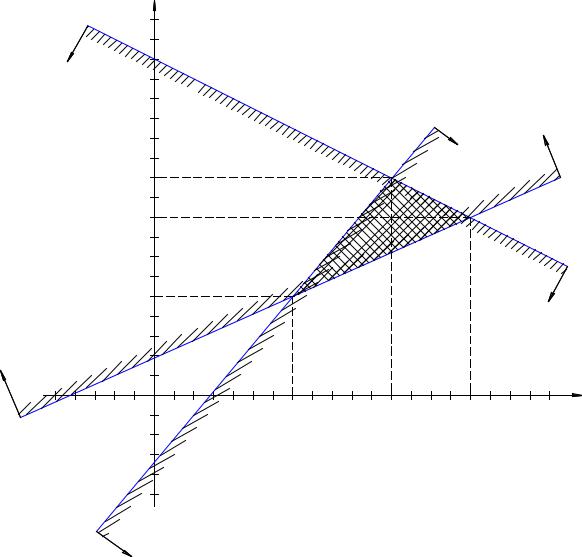
Г
			Задача 34. Построить на плоскости область решений системы
линейных неравенств.
	о
м					(1)
	6x −5y ≥17,
			тов
а					(2)
	x + 2y ≤ 34,
газ					(3)
−		4x +9y ≥17.
			Решениеы:
			Строим область решений системы. Нумеруем ограничения задачи. В
	и			ек
прямоугольной д картовой системе координат (см. рис.) строим прямую
http://www
			н
6х−5у =17 ( L1 ), соответствующую ограничению (1). Находим, какая из двух
полуплоскостей, на						т рые эта прямая делит всю координатную плоскость,
					о
			ра
является обл стью реше ий неравенства (1). Для этого достаточно
			бнт
координаты к кой-либо очки, не лежащей на прямой, подставить в
неравенство. Так как прямая L1 не проходит через начало координат,
				о		р
подставляем к					рдинаты т чки О (0, 0) в первое ограничение 0 + 0 ≥ 17.
			.		т		о
Получаем неравенс во 0 ≥ 17. С едовательно, точка О не лежит в
полуплоскостиna4решений. Таким образом, стрелки на концах прямой L1
					-			л
должны быть направлены в поьуплоскость, не содержащую точку О.
Аналогично строим прямые х + 2у = 34 ( L2 ), − 4х+9у =17 ( L3 ), и области
			.					ны
решений ограничений (2) и (3). Находим общую часть полуплоскостей
					na4
решений; полученную область допустимых решений отметим (см. рис.)
			by/					. е
штриховкой.

y	by	р
	-
L2	лу		або
	ч		т
	ш		ы
	и
11				L3
	е
9	це
			н
5			ы
			и
		7	ка12	16	x
			ч
			е
			ств
	L1			о

Г
Найдем теоретически точки пересечений прямых:
		о
м			тов
а6x −5y =17				6(34 −		2y) −5y =17	y =11
газ					x = 34 − 2y			x =12
	x		+ 2y = 34

	ы					у −17) − 20y = 68
6x −5y	=17		6(9					y = 5
и
− 4х+9у =17		е					x = 7
			x =			9у −17
http://www
н						4
			к
			о
	ра					34 − 2у			y = 9
x + 2y = 34			х =
	у =17				нт					16
− 4х+9			− 4(34 − 2у) +9у =17						x =
.бото
						р
na4				-			ль
	.						ны
				na4
	by/						. е
						by			р
					-
						лу			або
						ч				т
							ш			ы
							и
							е
								це
									н
									ы
										и

ка ч е ств о