
Математика, контрольная работа, 3 семестр 1 вариант
.doc-
Построить на плоскости область допустимых решений системы линейных неравенств и найти максимальное и минимальное значения линейной функции цели в этой области:

![]()
Решение.
Построим на плоскости
![]() многоугольник решений. Для этого в
неравенствах системы ограничений и
условиях неотрицательности переменных
знаки неравенств заменим на знаки точных
равенств.
многоугольник решений. Для этого в
неравенствах системы ограничений и
условиях неотрицательности переменных
знаки неравенств заменим на знаки точных
равенств.

Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение (рис.1.).

Рис.1.
Многоугольником решений задачи является пятиугольник АВСДЕF, координаты точек которого удовлетворяют условию неотрицательности и неравенствам системы ограничений задачи.
Для нахождения точек экстремума построим
начальную прямую
![]() и вектор
и вектор
![]() .
.
Передвигая прямую
![]() параллельно самой себе в направлении
вектора
параллельно самой себе в направлении
вектора
![]() ,
найдем точку A, в
которой начальная прямая принимает
положение опорной прямой.
,
найдем точку A, в
которой начальная прямая принимает
положение опорной прямой.
Следовательно, в точке A целевая функция принимает максимальное значение, так как точка A получена в результате пересечения прямых (2) и (5), то ее координаты удовлетворяют уравнениям этих прямых:

Решив систему уравнений, получим:
![]()
![]()
Для нахождения минимального значения
целевой функции задачи перемещаем
начальную прямую в направлении,
противоположному вектору
![]() .
Начальная прямая сливается с одной из
сторон многоугольника решений, со
стороной (1). Целевая функция принимает
минимальное значение во множестве точек
прямой (1), ограниченной точками D
и E. Множество точек
отрезка DE имеет одинаковое
минимальное значение целевой функции:
.
Начальная прямая сливается с одной из
сторон многоугольника решений, со
стороной (1). Целевая функция принимает
минимальное значение во множестве точек
прямой (1), ограниченной точками D
и E. Множество точек
отрезка DE имеет одинаковое
минимальное значение целевой функции:
![]() .
.
Найдем координаты угловых точек В, C, D, E, F. Для этого решим следующие системы уравнений:





В результате получим координаты точек:
В (![]() ),
С (3;0), D(5;0), E(6;0,4),
F(6;1,75).
),
С (3;0), D(5;0), E(6;0,4),
F(6;1,75).
Вычислим значение целевой функции во всех угловых точках многоугольника решений АВСДЕ:

-
Для реализации трех групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве
 единиц. При этом для продажи 1 группы
товаров на 1 тыс. руб. товарооборота
расходуется ресурса первого вида в
количестве
единиц. При этом для продажи 1 группы
товаров на 1 тыс. руб. товарооборота
расходуется ресурса первого вида в
количестве
 единиц, ресурса второго вида в количестве
единиц, ресурса второго вида в количестве
 единиц, ресурса третьего вида в количестве
единиц, ресурса третьего вида в количестве
 единиц. Для продажи 2 и 3 групп товаров
на 1 тыс. руб. товарооборота расходуется
соответственно ресурса первого вида
в количестве
единиц. Для продажи 2 и 3 групп товаров
на 1 тыс. руб. товарооборота расходуется
соответственно ресурса первого вида
в количестве
 и
и
 единиц, ресурсов второго вида в количестве
единиц, ресурсов второго вида в количестве
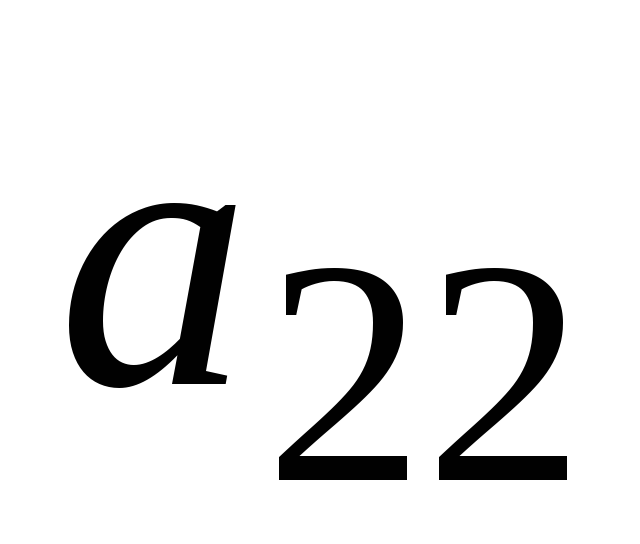 и
и
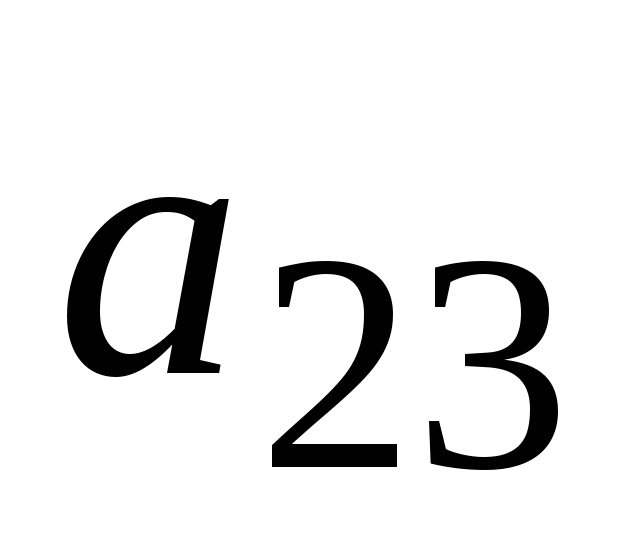 единиц, ресурсов третьего вида в
количестве
единиц, ресурсов третьего вида в
количестве
 и
и
 единиц. Прибыль от продажи трех групп
товаров на 1 тыс. руб. товарооборота
составляет соответственно
единиц. Прибыль от продажи трех групп
товаров на 1 тыс. руб. товарооборота
составляет соответственно
 (тыс. руб.)
(тыс. руб.)
Определить плановый объем и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.
![]()
Решение.
Составим таблицу:
|
Виды материально-денежных ресурсов |
Норма затрат материально-денежных ресурсов на ед. товарооборота, тыс. руб. |
Объем ресурсов
|
||
|
1 группа |
2 группа |
3 группа |
||
|
Первый вид ресурсов |
5 |
8 |
4 |
400 |
|
Второй вид ресурсов |
5 |
5 |
6 |
300 |
|
Третий вид ресурсов |
10 |
2 |
5 |
200 |
|
Прибыль, т. руб. |
4 |
3 |
2 |
max |
Запишем математическую модель задачи.
Определим
![]() ,
который удовлетворяет условиям
,
который удовлетворяет условиям

и обеспечивают максимальное значение
целевой функции
![]()
Для построения первого опорного плана систему неравенств приведем к системе уравнений.

В матрице этой системы уравнений
![]() имеет вид:
имеет вид:

векторы А4, А5, А6 – линейно независимы, так как определить, составленный из компонент этих векторов, отличен от нулю:

Соответствующие этим векторам переменные х4, х5, х6 будут базисными.
Решим систему уравнений относительно базисных переменных.

Фуцию цели запишем в виде:
![]() .
.
Полагая, что свободные переменные х1=0,
х2=0, х3=0, получим первый
опорный план
![]() ,
,
![]() ,
в котором базисные переменные х4=400,
х5=300, х6=200, следовательно
товары не продаются и прибыль равна
нулю, а ресурсы не используются.
,
в котором базисные переменные х4=400,
х5=300, х6=200, следовательно
товары не продаются и прибыль равна
нулю, а ресурсы не используются.
Запишем первый опорный план в симплексную таблицу:
|
План |
Базисные переменные |
Результаты плана |
Значение коэффициента при переменных |
|
|||||
|
х1 |
х2 |
х3 |
х4 |
х5 |
х6 |
||||
|
I план |
х4 х5 х6 |
400 300 200 |
5 5 10 |
8 5 2 |
4 6 5 |
1 0 0 |
0 1 0 |
0 0 1 |
80 60 20 |
|
Инд. строка |
|
0 |
-4 |
-3 |
-2 |
0 |
0 |
0 |
|
|
II план |
х4 х5 х1 |
300 200 20 |
0 0 1 |
7 4 0,2 |
1,5 3,5 0,5 |
1 0 0 |
0 1 0 |
-0,5 -0,5 0,1 |
42,86 50 100 |
|
Инд. строка |
|
80 |
0 |
-2,2 |
0 |
0 |
0 |
0,4 |
|
|
III план |
х2 х5 х61 |
300/7 200/7 80/7 |
0 0 1 |
1 0 0 |
0,21 2,64 0,46 |
0,14 -0,57 -0,029 |
0 1 0 |
-0,071 -0,21 0,11 |
|
|
Инд. строка |
|
1220/7 |
0 |
0 |
0,47 |
0,314 |
0 |
0,243 |
|
Первый опорный план не оптимальный, так как в индексной строке находятся отрицательные коэффициенты -4, -3, -2.
За ведущий столбец выберем столбец, соответствующий переменной х1, так как сравниваемая по модулю имеем: |-4| > {|-3|, |-2|}.
Рассчитываем значения
![]() по строкам, как частное от деления
по строкам, как частное от деления
![]() и выбираем наименьшее:
и выбираем наименьшее:
![]()
Следовательно, третья строка является ведущей. Элемент 10 находится на пересечении ведущего столбца и ведущей строки и выделен.
Формируем следующую симплексную таблицу. Вместо переменной х6 в план II войдет переменная х1. Строка, соответствующая переменной х6 в плане II, получена в результате деления всех элементов строки х6 плана I на разрешающий элемент РЭ = 10. на месте разрешающего элемента в плане II получаем 1. в остальных клетках столбца х1 плана II записываем нули.
Таким образом в новом плане II заполнены
строки х1 и столбец х1. Все
остальные элементы нового плана II,
включая элементы индексной строки,
определяются по правилу прямоугольника.
Для этого выбираем из старого плана 4
числа, которые расположены в вершинах
прямоугольника и всегда включают
разрешающий элемент РЭ = 10. Во второй
вершине по диагонали находится старое
значение элемента, например, значение
целевой функции
![]() ,
которое указывает на место расположения
нового НЭ в новом плане II. Третий элемент
А = 200 и четвертый элемент В = -4 завершают
построение прямоугольника в недостающих
двух вершинах и расположены по другой
диагонали. Значение нового элемента в
плане II находится из выражения:
,
которое указывает на место расположения
нового НЭ в новом плане II. Третий элемент
А = 200 и четвертый элемент В = -4 завершают
построение прямоугольника в недостающих
двух вершинах и расположены по другой
диагонали. Значение нового элемента в
плане II находится из выражения:
![]()
Элементы строки определяются аналогично:

Все элементы, расположенные на пересечении строк и столбцов, соответствующих одноименным базисным элементам равны 1, остальные элементы столбца в базисах векторов, включая индексную строку, равны 0. Аналогично проводятся расчеты по всем строкам таблицы, включая индексную.
Выполняя последовательно все этапы алгоритма, формируем план II.
На третьей итерации таблицы 3 получаем
план III, который является оптимальным
так как все коэффициенты в индексной
строке
![]() .
.
Оптимальный план можно записать так:
![]()
Согласно этому плану необходимо продать
![]() единиц
товара первой группы и
единиц
товара первой группы и
![]() единиц
второй группы. Максимальная прибыль
при этом будет равна
единиц
второй группы. Максимальная прибыль
при этом будет равна
![]() тыс.руб. В
оптимальном плане среди базисных
переменных находится дополнительная
переменная х5. Это указывает, что
ресурсы второго вида недоиспользованы
на
тыс.руб. В
оптимальном плане среди базисных
переменных находится дополнительная
переменная х5. Это указывает, что
ресурсы второго вида недоиспользованы
на
![]() единиц, так как переменная х5 была
введена в первое ограничение задачи,
характеризующее собой использование
этого ресурса.
единиц, так как переменная х5 была
введена в первое ограничение задачи,
характеризующее собой использование
этого ресурса.
В индексной строке III плана в столбцах переменных х3, х4, х6, не вошедших в состав базисных, получены ненулевые элементы, поэтому оптимальный план задачи линейного программирования является единственным.
-
Используя вариант предыдущего контрольного задания необходимо:
-
к прямой задаче планирования товарооборота, решаемой симплексным методом, составить двойственную задачу линейного программирования;
-
установить сопряженные пары переменных прямой и двойственной задач;
-
согласно сопряженным парам переменных из решения прямой задачи получить решение двойственной задачи, в которой производится оценка ресурсов, затраченных на продажу товаров.
Решение
-
Двойственная задача.
Определить оценку единицы каждого вида
ресурсов, чтобы при заданных объемах
ресурсов
![]() ,
прибыли
,
прибыли
![]() ,
минимизировать оценку всех ресурсов
торгового предприятия, затраченных на
организацию торгового процесса.
,
минимизировать оценку всех ресурсов
торгового предприятия, затраченных на
организацию торгового процесса.
Определить
![]() ,
который удовлетворяет условиям –
ограничениям:
,
который удовлетворяет условиям –
ограничениям:

и обеспечивает минимальное значение целевой функции
![]()
2.Сопряженные пары прямой и двойственной задачи.

-
Решение двойственной задачи
Базисные переменные
![]() решения прямой задачи имеют коэффициенты
решения прямой задачи имеют коэффициенты
![]() .
.
Исходя из соответствия между переменными взаимно-двойственных задач получим:
![]()
-
Поставщики товара – оптовые коммерческие предприятия
 имеют запасы товаров соответственно
в количестве
имеют запасы товаров соответственно
в количестве
 ед. и розничные торговые предприятия
ед. и розничные торговые предприятия
 - подали заявки на закупку товаров в
объемах соответственно:
- подали заявки на закупку товаров в
объемах соответственно:
 .
Тарифы перевозок единицы груза с каждого
из пунктов поставки в соответствующие
пункты потребление заданы в виде матрицы
.
Тарифы перевозок единицы груза с каждого
из пунктов поставки в соответствующие
пункты потребление заданы в виде матрицы
 .
.
Найти такой план перевозки груза от поставщиков к потребителям, чтобы совокупные затраты на перевозку были минимальными.


Решение
Проверим необходимое и достаточное условие разрешимости задачи.

Как видно, суммарная потребность груза в пунктах назначения превышает запасы груза на трех базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) базу А4 с запасом груза, равным 790 – 780 = 10 (ед.). Тарифы перевозки единицы груза из базы А4 во все магазины полагаем равны нулю.
Занесем исходные данные в распределительную таблицу:
|
|
В1 |
В2 |
В3 |
В4 |
Потенциалы
|
||||||
|
|
|
|
|
|
|||||||
|
А1 |
|
3 |
3 |
|
16 |
|
17 |
2 |
2 |
|
|
|
1 |
|
|
- |
||||||||
|
А2 |
|
3 |
21 |
21 |
19 |
|
15 |
|
2 |
|
|
|
1 |
75 |
|
+ |
||||||||
|
А3 |
|
3 |
11 |
|
13 |
11 |
4 |
|
3 |
|
|
|
255 |
|
125 |
|
||||||||
|
А4 |
|
3 |
0 |
|
0 |
|
0 |
|
0 |
|
|
|
10 |
|
|
|
||||||||
|
Потенциалы
|
|
|
|
|
|
||||||
Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
Среди тарифов из всей таблицы наилучшим
является с14 = 2, поэтому в клетку
А1В4 направляем максимально
возможный груз. Он равен А1В4
![]() .
Тогда х14 = 200 и из базы А1 не
вывезен, груз 10 ед., а потребность магазина
В4 удовлетворена полностью. Столбец
таблицы В4 выходит из рассмотрения.
Из оставшихся тарифов строки наименьший
– с11 = 3. В клетку А1В1
направляем максимально возможный груз,
равный
.
Тогда х14 = 200 и из базы А1 не
вывезен, груз 10 ед., а потребность магазина
В4 удовлетворена полностью. Столбец
таблицы В4 выходит из рассмотрения.
Из оставшихся тарифов строки наименьший
– с11 = 3. В клетку А1В1
направляем максимально возможный груз,
равный
![]() .
Тогда строка А1 выходит из
рассмотрения, поскольку из базы А1
вывезен весь груз. Из оставшихся тарифов
наилучший с33 = 4. В клетку А3В3
направляем груз, равный
.
Тогда строка А1 выходит из
рассмотрения, поскольку из базы А1
вывезен весь груз. Из оставшихся тарифов
наилучший с33 = 4. В клетку А3В3
направляем груз, равный
![]() .
При этом вычеркивается столбец В3
из рассмотрения. Из оставшихся тарифов
наименьший с31 = 11. В клетку А3В1
направляем груз, равный
.
При этом вычеркивается столбец В3
из рассмотрения. Из оставшихся тарифов
наименьший с31 = 11. В клетку А3В1
направляем груз, равный
![]() .
При этом из третьей базы все вывезено.
Из оставшихся тарифов наилучший с22
= 19. Направим от поставщика А2 в
магазин В2
.
При этом из третьей базы все вывезено.
Из оставшихся тарифов наилучший с22
= 19. Направим от поставщика А2 в
магазин В2
![]() .
Спрос магазина В2 удовлетворен.
На базе А2 осталось 115 единиц.
Направляем их в В1
.
Спрос магазина В2 удовлетворен.
На базе А2 осталось 115 единиц.
Направляем их в В1
Потребность первого магазина не удовлетворена на 10 ед. Нераспределенный груз А4 направляем в клетку А4В1, х41 = 10.
В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план удовлетворяет системе ограничений транспортной задачи.
Посчитаем число занятых клеток таблицы,
их -7, а должно быть
![]() .
Следовательно, опорный план является
невырожденным.
.
Следовательно, опорный план является
невырожденным.
Определяем значение целевой функции первого опорного плана.
![]()
Проверим оптимальность опорного плана.
Найдем потенциалы
![]() по занятым клеткам таблицы, решая систему
уравнений, полагая что
по занятым клеткам таблицы, решая систему
уравнений, полагая что
![]()
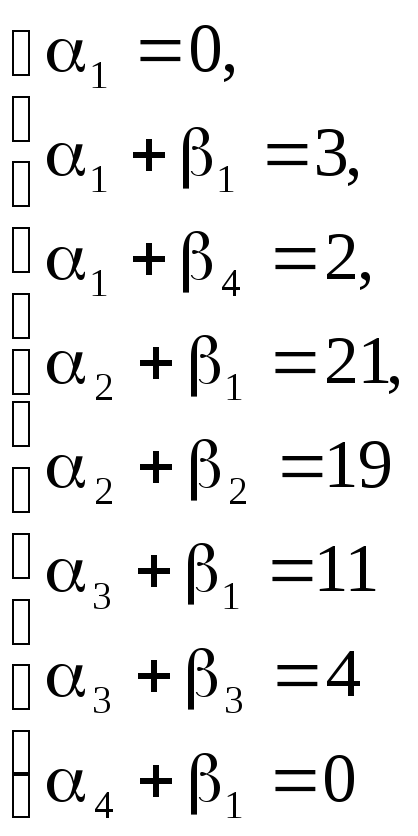
![]()

![]()



 0
+
0
+ 200
200 15
-
15
-