Лекции 3

Симплекс-метод решения задачи ЛП

В основе метода лежит перебор базисных решений (т.е. вершин допустимой области) до нахождения оптимального решения. Причем алгоритм организован так, что бы быстрей прийти к оптимуму, не перебирая все вершины.

Ценность метода - его формализованность и возможность использования его для разработки программного обеспечения.

Приведение задачи ЛП к стандартной форме

Пусть дано - ограничений, - переменных и целевая функция

Требуется определить при котором целевая функция достигает максимума или минимума.

Ограничения записываются в виде системы уравнений

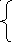
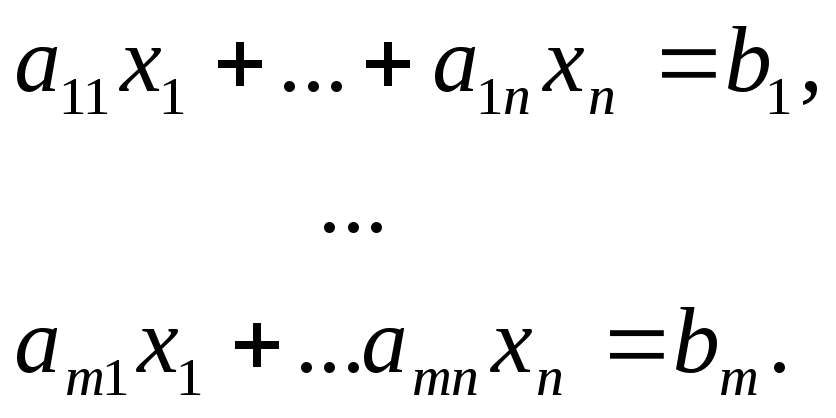
При этом все переменные 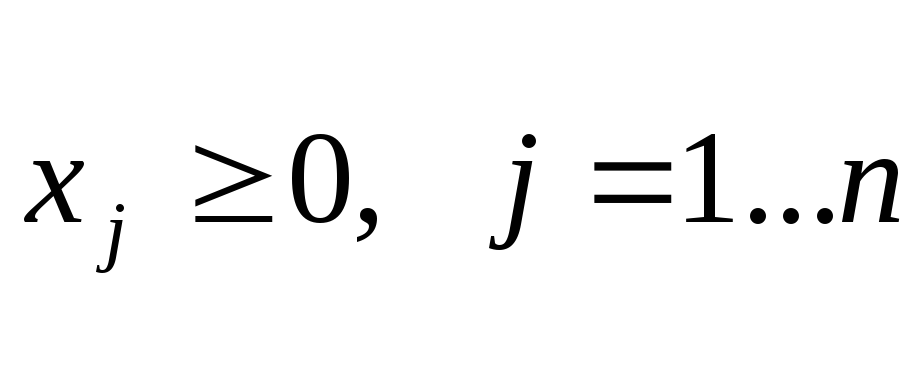и коэффициенты Последнее легко выполнить, умножив при необходимости уравнения на –1, т.к. на коэффициенты никаких ограничений не накладываются.

В матричной форме где символ - вектор,

- матрица.

Замечание 1. Ограничения записанные в виде неравенств, превращаются в равенство введением дополнительных (избыточных или остаточных) переменных. Например, превращается в При этом Если знак , то переменная войдет с отрицательным знаком.

Пусть тогда но Так, приведенное в примере неравенство можно превратить в уравнение

Замечание 2. Исходные переменные, в принципе, могут быть и меньше нуля. Тогда переменную заменяют двумя переменными Естественно  но .

Вернемся к примеру и запишем условия в стандартной форме

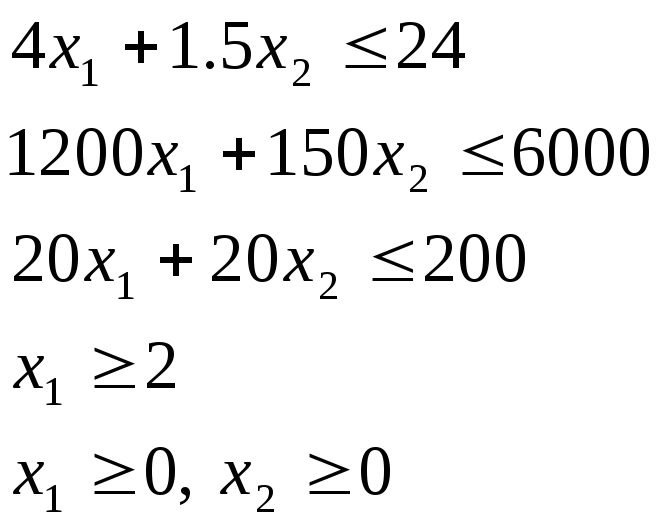
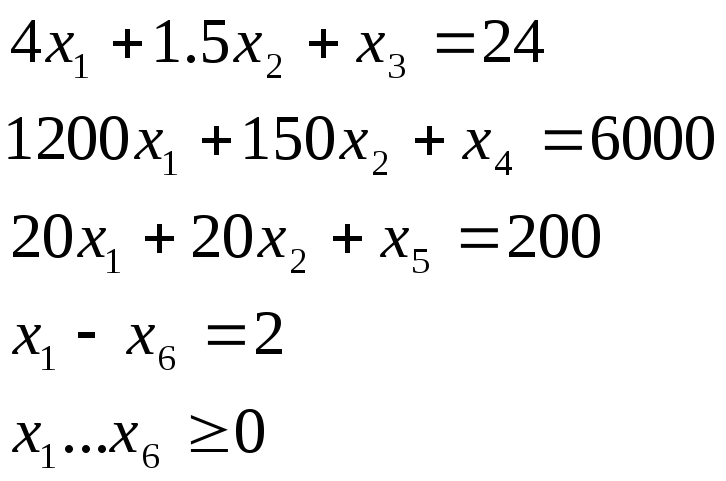
Следует обратить внимание, что

а) избыточные переменные входят только в одно уравнение,

б) коэффициент перед избыточным переменным +1, но может и 1, это кстати создаст дополнительные трудности.

Необходимо отметить, что дополнительные переменные имеют четкий смысл: показывает, сколько земли осталось свободной, - сколько осталось денег, а - сколько осталось времени. Переменная показывает, на сколько больше (по сравнению с контрактом ) было приобретено бычков.

Например, при получаем все ресурсы не использованы.

При мы получим т.е. ресурсы по земле и времени исчерпаны полностью, денег осталось 720 у.е.

Вернемся к системе уравнений, называемых системой ограничений задачи ЛП.

…

Мы имеем переменных и уравнений. В задаче ЛП . Случай решается методами обычной алгебры: если определитель отличен от нуля, то имеется одно решение, если равен нулю, то бесконечное множество.

Случай  (число переменных меньше уравнений) не имеет конкретного решения. Так как либо уравнения противоречивы (например, ), либо тождественны (например, - фактически одно уравнение и ).

В нашем случае число переменных больше числа уравнений и мы имеем бесконечное множество решений, из которых мы должны выбрать такое, что бы целевая функция принимала максимальное (или минимальное) значение и при этом

Базисные решения

Любой набор удовлетворяющей системе из уравнений будем называть решением. Любое решение с неотрицательными значениями переменных будем называть допустимым решением.

Так как  можно переменных положить, например, равными нулю и решать систему относительно переменных обычными методами алгебры. Полученное при этом решение называть базисным.

Базисом называется любой набор из m переменных, такой, что определитель составленный из коэффициентов при этих переменных не равен нулю.

Эти m переменных называются базисными. Остальные переменные называются небазисными или свободными. Их можно положить равным нулю. Таким образом, если положить все свободные переменные равными нулю и решить систему относительно базисных переменных, то получим базисное решение.

Однако, среди решений могут быть отрицательные значения переменных, такие решения будем называть недоступными.

Доступным базисным решением является такое базисное решение, при котором все базисные переменные принимают неотрицательное значение, т.е. допустимое базисное решение – это решение системы m уравнений для n переменных, такое, что

1. базисные переменные

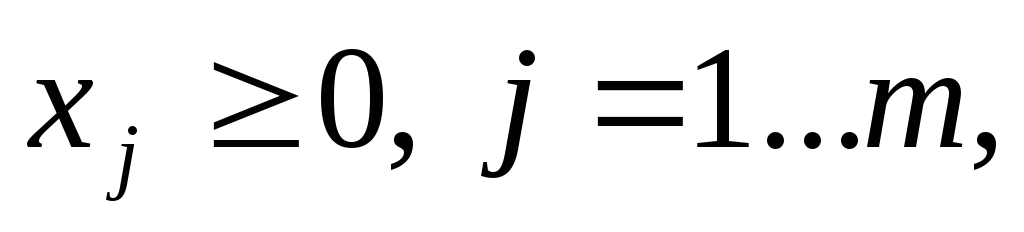
2. свободные переменные

Канонический вид стандартной формы задачи ЛП

Система ограничений должна быть записана в следующем виде:

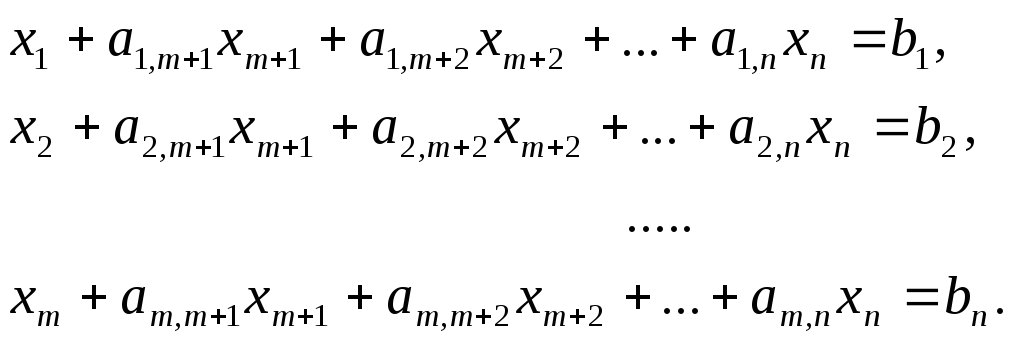
Переменные входящие с единичными коэффициентами только в одно уравнение, являются базисными, остальные свободными. Их можно положить равными нулю.

Тогда для 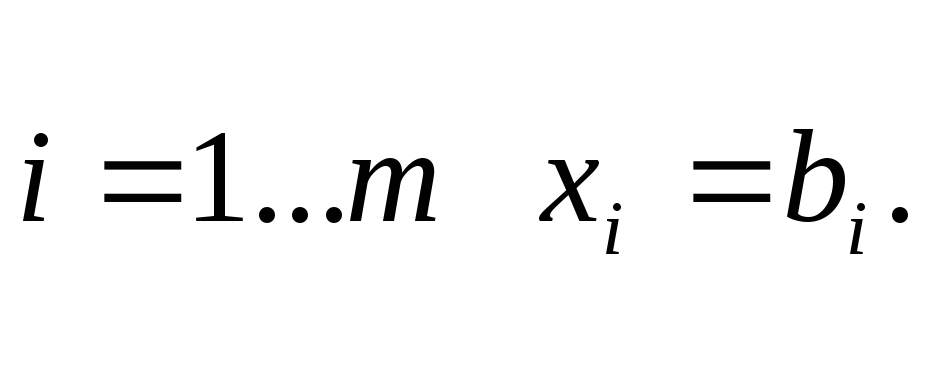Это базисное решение. Так как то , следовательно, это допустимое базисное решение.

Для приведения системы к каноническому виду можно использовать:

1) умножение любого уравнения на любое число отличное от нуля,

2) сложение любых систем уравнений, умноженных на любое число отличное от нуля.

В рассматриваемом примере

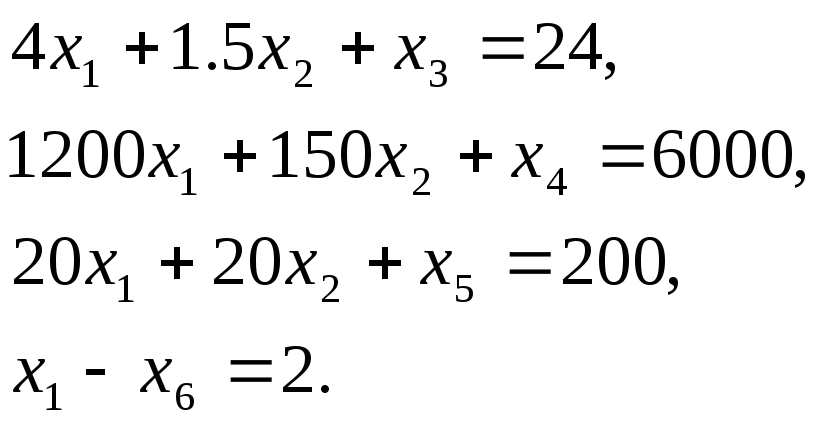
Сразу не удастся записать в каноническом виде. Мешает уравнение т.к. входит со знаком минус.

Если бы не было ограничений то все было бы проще. Было бы три уравнения, 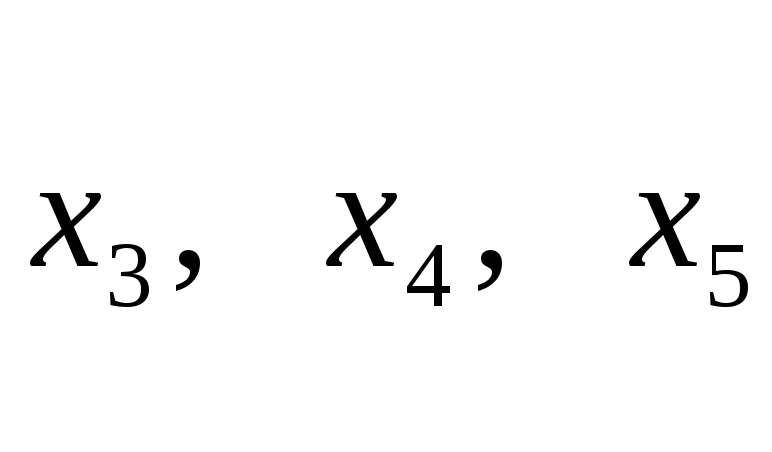- базисные переменные, - свободные, Это одно из допустимых базисных решений.

Хотя прибыль но все равно это решение можно использовать как начальное базовое допустимое решение (соответствующее началу координат на рис1).

Наличие условия на первый взгляд, ничего не меняет, но приводит к следующему - базисные, свободные. Но при этом т.е. решение не является допустимым.

Поэтому, рассмотрим в начале случай, когда нам сразу удалось получить ограничения в каноническом виде, например, в системе ограничений были неравенства только типа «меньше или равно». Такой метод получил название одноэтапного симплекс-метода. Решение более сложных задач реализуется с помощью двухэтапного симплекс-метода, который мы рассмотрим отдельно.

Ниже приводится алгоритм одноэтапного симплекс-метода и дана таблица симплекс-метода.

11