1.1 Изучить разложение в ряд Фурье последовательности прямоугольных импульсов. Проанализировать явление Гиббса.

1.2 Реализовать разложение в ряд Фурье пилообразного сигнала и последовательности треугольных импульсов.

1.3 Сделать общие выводы.

Часть 2

Цель работы: углубление теоретических знаний, полученных в ходе изучения преобразования Фурье (Fourier Transform)

Необходимые теоретические сведения.

Изменяя период Т и длительность импульса как показано на рис. 7, можно изменять спектр сигнала. С увеличением периода гармоники сближаются, не изменяя форму огибающей.

Рис.7 – Изменение спектра

Смоделируем одиночный прямоугольный импульс, периодическую последовательность импульсов с периодом Т и 10Т .

t = 0:.0314:25;

t1 = -2:.01:2;

x=square(pi*t);

y= square(2*pi*t/10, pi*pi);

z = rectpuls(2*pi*t1/10);

subplot(4,2,1); plot(t,x)

subplot(4,2,2); plot(t,y)

subplot(4,2,3); plot(t1,z)

Проведем спектральный анализ полученных сигналов. Непериодические процессы — таковыми являются информационные сигналы, одиночные импульсы, хаотические колебания (шумы) — обладают сплошным или непрерывным спектром. Интуитивно к такому выводу можно прийти, представляя одиночный импульс частью периодической последовательности, период которой неограниченно увеличивается. Действительно, при увеличении интервала между импульсами гармоники на спектральных диаграммах периодических последовательностей импульсов сближаются: чем реже следуют импульсы, тем меньше расстояние между соседними гармониками (оно равно 1/T). Спектр одиночного импульса (предельный случай увеличения периода) становится непрерывным, и вводится он не рядами, а интегралами Фурье.

Преобразование Фурье (Fourier transform) является инструментом спектрально­го анализа непериодических сигналов.

В описанных ниже функциях реализован особый метод быстрого преобразования Фурье (БПФ) — Fast Fourier Transform (FFT), позволяющий резко уменьшить число арифметических операций в ходе приведенных выше преобразований. Метод особенно эффективен, если число обрабатываемых элементов (отсчетов) составляет 2ⁿ, где n — целое положительное число. В MatLab используются следующие функции:

fft(X) — возвращает для вектора X дискретное преобразование Фурье, по возможности используя алгоритм быстрого преобразования Фурье. Если X — матрица, функция fft возвращает преобразование Фурье для каждого столбца матрицы;

fft(X.n) — возвращает n-точечное преобразование Фурье. Если длина вектора X меньше n, то недостающие элементы заполняются нулями. Если длина X больше п, то лишние элементы удаляются. Когда X — матрица, длина столбцов корректируется аналогично;

ft(X,[ Ldirn) и fft(X,n,dim) — применяют преобразование Фурье к одной из размерностей массива в зависимости от значения параметра dim.

Возможно одномерное обратное преобразование Фурье, реализуемое следующими функциями:

ifft(F) — возвращает результат дискретного обратного преобразования Фурье вектора F. Если F — матрица, то ifft возвращает обратное преобразование Фурье для каждого столбца этой матрицы;

ifft(F.n) — возвращает результат n-точечного дискретного обратного преобразования Фурье вектора F;

ifft(F.[ ],dim) иу = ifft(X,n,dim) — возвращают результат обратного дискретного преобразования Фурье массива F по строкам или по столбцам в зависимости от значения скаляра dim.

Для любого X результат последовательного выполнения прямого и обратного преобразований Фурье ifft(fft(x)) равен X с точностью до погрешности округления. Если X — массив действительных чисел, ifft(fft(x)) может иметь малые мнимые части.

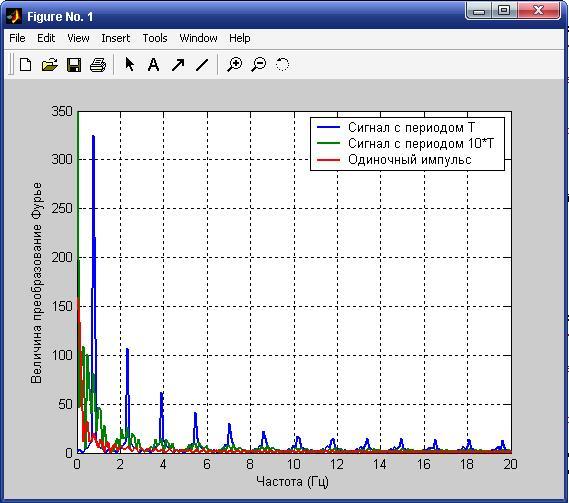
Получим спектры смоделированных сигналов.

t = 0:.0314:20;

x=square(pi*t);

y= square(2*pi*t/10, pi*pi);

z = rectpuls(2*pi*t/10);

Fs=50;

X = fft(x,512);

Y = fft(y,512);

Z = fft(z,512);

w = (0:255)/256*(Fs/2);

plot(w,abs([X(1:256)' Y(1:256)' Z(1:256)'])); grid;

legend ('Сигнал с периодом Т', 'Сигнал с периодом 10*Т',

'Одиночный импульс');

xlabel('Частота(Гц)');

ylabel('Величина Фурье преобразования');

Вызовем программу SPTool (Signal Processing Tool). Импортируем смоделированные сигналы и рассчитаем спектр сигнала. С этой целью выделяем сигнал в списке сигналов и нажмите кнопку Create, расположенную под списком спектров. В окне Spectrum Viewer в поле Parameters нужно указать метод спектрального анализа. Указываем метод ДПФ (используется быстрое преобразование Фурье БПФ (FFT)). Указав метод, следует щёлкнуть мышью по кнопке Apply. Будет выведен график спектральной плотности мощности. Имеется возможность выводить спектры в линейном или в логарифмическом масштабе (меню Options).

Непрерывным (сплошным) является спектр хаотических (шумовых) колебаний. В этом случае спектральная характеристика, как функция частоты, также представляет собой хаотический (случайный) процесс, статистические параметры которого определяются спецификой конкретного случайного временного процесса. Сформируем сигнал, содержащий регулярные составляющие с частотами 50 Гц и 120 Гц и случайную аддитивную компоненту с нулевым средним.

t = 0:0.001:0.6; x = sin(2 * pi * 50 * t) + sin(2 * pi * 120 * t); y = x + 2 * randn(size(t)); plot(y(1:50)), grid

По виду сигнала, трудно сказать, каковы частоты его регулярных составляющих. Реализуя одномерное преобразование Фурье этого сигнала на основе 512 точек и построив график спектральной плотности, можно выделить две частоты, на которых амплитуда спектра максимальна. Это частоты 120 и 50 Гц.

Y = fft(y, 512); Pyy = Y.*conj(Y)/512; f = 1000 * (0:255)/512; figure(2), plot(f, Pyy(1:256)), grid

ЗАДАНИЕ 2