Московский государственный технический университет имени Н.Э. Баумана

А.Ю. Горячкина, И.А. Горюнова

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ ПЛОСКИХ ФИГУР

Рекомендовано Научно-методическим советом МГТУ им. Н.Э. Баумана в качестве учебного пособия

Москва Издательство МГТУ им. Н.Э. Баумана

2012

1. ВВОДНАЯ ЧАСТЬ. ГЕОМЕТРИЧЕСКИЕ МНОЖЕСТВА

Контуры многих машино- и приборостроительных деталей имеют сложную форму и состоят из линий различных видов: прямых, дуг окружностей и лекальных кривых.

Для того чтобы изобразить на чертеже очертания предмета, которые вполне соответствовали бы его действительной форме, необходимы твердые знания принципов геометрического построения плоских фигур и умение применять их в каждом отдельном случае.

Одним из способов решения задач на геометрические построения является использование геометрических множеств.

Геометрическое множество точек плоскости — это множество, обладающее определенным геометрическим свойством или свойствами, общими для всех точек. Это означает, что все точки, принадлежащие фигуре, удовлетворяют заданному свойству, и, наоборот, все точки, удовлетворяющие заданному свойству, принадлежат фигуре. Другими словами, точка принадлежит фигуре в том и только в том случае, когда для нее выполняется заданное свойство.

Использование геометрических множеств при решении задач состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X, удовлетворяющую двум условиям. Геометрическое множество точек, удовлетворяющих первому условию, есть некоторая фигура A, а геометрическое множество точек, удовлетворяющих второму условию, есть некоторая фигура B. Искомая точка X принадлежит геометрическим множествам A и B, т. е. является точкой пересечения двух множеств.

Рассмотрим геометрические множества точек, которыми будем пользоваться при геометрических построениях на плоскости.

Геометрическое множество точек плоскости (рис. 1), удаленных от заданной точки O на заданное расстояние R, есть по определению окружность m (O,R).

Геометрическое множество точек плоскости (рис. 2), равноудаленных от двух заданных точек A и B, есть прямая m, проходящая через середину отрезка AB и перпендикулярная этому отрезку.

3

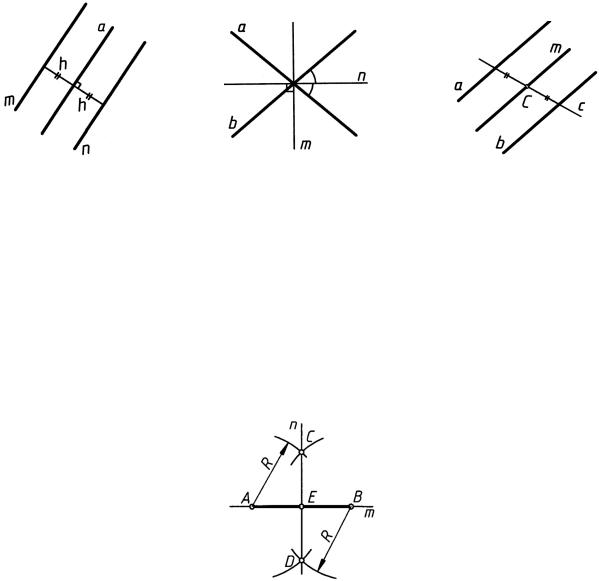
Геометрическим множеством точек плоскости (рис. 3), находящихся от заданной прямой a на заданном расстоянии h, являются две прямые m и n, параллельные прямой a и находящиеся от нее на заданном расстоянии h.

Геометрическое множество точек плоскости (рис. 4), равноудаленных от двух данных пересекающихся прямых a и b, представляет собой две взаимно перпендикулярные прямые m и n, являющиеся биссектрисами углов, образованных прямыми a и b.

Геометрическое множество точек плоскости (рис. 5), равноудаленных от двух данных параллельных прямых a и b, есть прямая m, параллельная прямым a и b, проходящая через точку C — середину отрезка секущей c.

2.ДЕЛЕНИЕ ОТРЕЗКОВ ПРЯМЫХ И УГЛОВ. ПЕРПЕНДИКУЛЯР К ПРЯМОЙ

2.1.Деление отрезка прямой пополам

Отрезок АВ прямой m (рис. 6) делится на две равные части перпендикуляром n, проведенным через точки пересечения C и D дуг окружностей радиуса R > 0,5AB с центрами соответственно в точках A и B. Точка E — середина отрезка АВ. Построения выполнены на основании теоремы о том, что серединный перпендикуляр к отрезку является геометрическим множеством точек, одинаково удаленных от концов этого отрезка.

Рис. 6

2.2. Деление отрезка прямой на заданное число частей

Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне. На основании этой теоремы выполняют геометрические построения.

4

Рис. 7

Отрезок АВ прямой m (рис. 7) разделен на семь частей посредством вспомогательного луча t, проведенного через точку A под острым углом к заданной прямой m. На луче t от точки A отложено заданное число (n = 7) равных отрезков произвольной длины, отмеченных точками 1, 2, . . . , 7. Последняя точка 7 соединена с точкой B, и из каждой точки деления луча t последовательно проведены прямые, параллельные прямой В7, до пересечения с прямой m. Полученные точки 1 , 2 , . . . , 7 делят отрезок АВ в искомом отношении.

2.3. Деление отрезка прямой на пропорциональные части

Это деление выполняют по аналогии с построением, представленным на рис. 7, с тем лишь отличием, что на вспомогательном луче t откладывают сумму отрезков, составляющих заданное отношение, например А2 : 2 В = 2 : 5 или А4 : 4 В = 4 : 3 (см. рис. 7). При построении основываются на теореме о том, что параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

2.4. Деление отрезка прямой в среднем и в крайнем отношении (правило золотого сечения)

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей, или, другими словами, меньший отрезок так относится к большему, как больший ко всему отрезку.

На рис. 8 отрезок АВ разделен в отношении АВ : АK = АK : KВ. Для построения отрезок АВ надо разделить пополам точкой С. В точке B восстановить перпендикуляр к отрезку АВ и отложить на нем отрезок ВМ = АС. На луче АМ от точки М отложить отрезок МN = ВМ = АВ/2. Затем из точки A радиусом АN на прямой АВ засечь точку K, являющуюся искомой, чтобы разделить отрезок в заданном отношении.

Рис. 8

5

2.5. Построение отрезков прямой с заданным отношением сторон

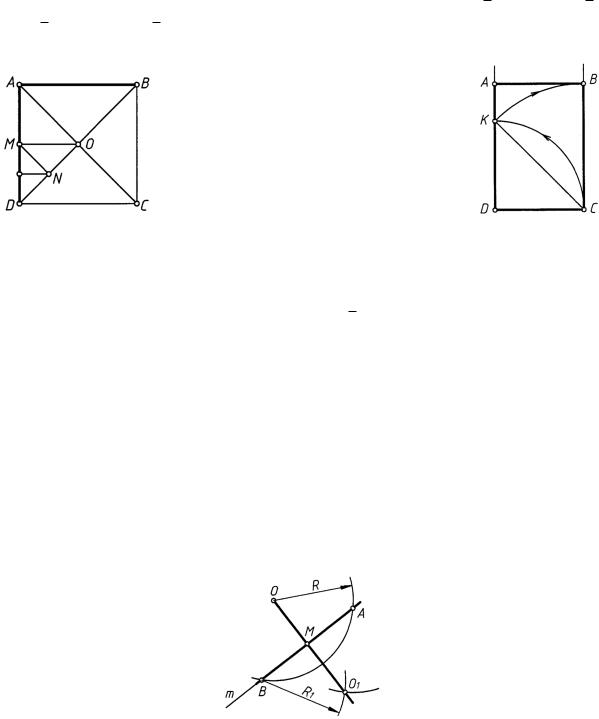
Диагональ DВ квадрата (рис. 9), сторона которого АВ, равна √2АВ; АВ = √2АО;

АО = √2ОМ; ОМ = √2МN и т. д.

На рис. 10 показано построение большой стороны BC прямоугольника по заданной короткой стороне DC. На перпендикуляре, восстановленном к отрезку DC в точке D, отложить DК = DC и построить CB = CК = √2DC. Это соотношение принято при образовании стандартных форматов чертежей: основой формата является прямоугольник, такой, что при делении большей его стороны пополам образуется прямоугольник с тем же отношением сторон, что и у исходного прямоугольника.

2.6. Построение перпендикуляра к прямой, проходящего через точку, лежащую вне этой прямой

Из точки O засечкой произвольного радиуса R отметить на прямой m точки A и B (рис. 11). Используя эти точки как центры, провести равными радиусами R1 дуги окружностей до их взаимного пересечения в точке O1. Отрезок ОО1 AB.

Рис. 11

2.7. Построение перпендикуляра к прямой в точке, принадлежащей данной прямой

Провести из произвольно выбранного центра O, расположенного вне данной прямой m, дугу окружности радиуса R = OA (рис. 12) и отметить на прямой m точку B

6

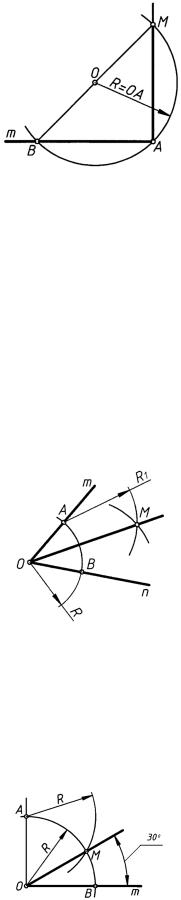
Рис. 12

ее пересечения с дугой. Построить диаметр BM и прямую MA; MA AB, так как вписанный в окружность и опирающийся на ее диаметр угол MAB прямой.

2.8. Деление угла пополам

Построение выполняют на основании теоремы о том, что биссектриса угла является геометрическим множеством точек, лежащих внутри данного угла и одинаково удаленных от его сторон.

Из вершины O заданного угла провести дугу произвольного радиуса R до пересечения ее со сторонами угла в точках A и B (рис. 13). Из полученных точек, как из центров, построить две дуги равных радиусов R1 до их взаимного пересечения в точке M. Биссектриса OM делит заданный угол пополам.

Рис. 13

2.9. Построение угла 30◦

Построить прямой угол (рис. 14). Из его вершины O провести дугу произвольного радиуса R. Из точки A тем же радиусом R сделать засечку на дуге AB в точке M. Угол MOB = 30◦ (поскольку треугольник AOM равносторонний, то угол AOM = 60◦).

Рис. 14

7

2.10. Построение угла 60◦

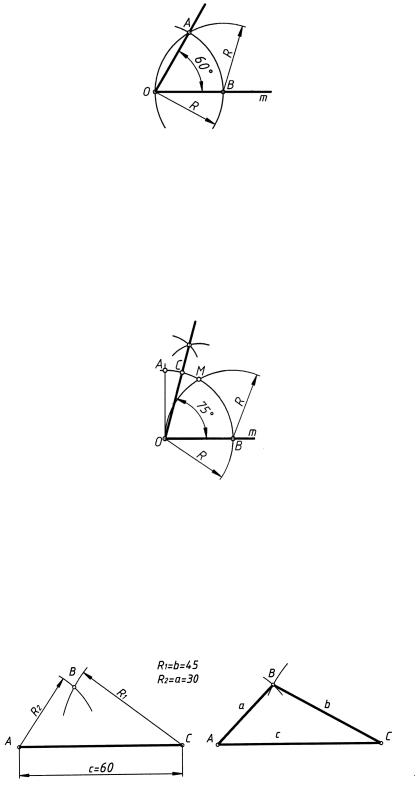
Из точки O на прямой m (рис. 15) провести дугу AB произвольного радиуса R. Из точки B на прямой m провести дугу окружности того же радиуса R до пересечения с первой дугой в точке A. Угол AOB = 60◦, так как треугольник AOB равносторонний.

Рис. 15

2.11. Построение угла 75◦

Построить прямой угол (рис. 16). Из его вершины O провести дугу AB произвольного радиуса R. Из точки B тем же радиусом R сделать засечку на дуге АВ в точке М. Угол BОМ = 60◦ необходимо дополнить, построив биссектрису угла МОA. Угол BОС = 75◦.

Рис. 16

2.12. Построение треугольника по трем заданным сторонам

Задан треугольник со сторонами a = 30 мм; b = 45 мм; c = 60 мм (рис. 17).

За основу построения можно принять любую сторону; в данном случае принята сторона c = AC = 60 мм.

Рис. 17

8