Рис. 52

5.УКЛОНЫ И КОНУСНОСТЬ

5.1.Уклоны. Обозначение, построение

Уклоном прямой по отношению к какой-либо другой прямой называется величина ее наклона к этой прямой, выраженная через тангенс угла между ними (рис. 53).

Рис. 53

Обозначение уклонов на чертеже выполняют в соответствии с ГОСТ 2.307–2011 «Нанесение размеров и предельных отклонений». Уклон указывают с помощью линиивыноски, на ее полке наносят знак уклона и его значение. Знак уклона должен соответствовать уклону определяемой линии: одна из прямых знака уклона должна быть горизонтальной, а другая — наклоненной в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака составляет примерно 30◦. На чертеже уклоны указывают либо в процентах (рис. 54), либо дробью в виде отношения двух чисел (рис. 55). Незначительный уклон допускается изображать на чертеже с увеличением.

Прямую заданного уклона b : a (по отношению к горизонтальной линии) проводят через точку А следующим образом (рис. 56). Из данной точки А проводят горизонтальный луч и на нем от точки А откладывают длину a (равную числовому значению делителя в выражении данного уклона) — получают точку В, через которую проводят вертикальную линию, и на ней от точки В откладывают длину b (численно равную значению делимого в выражении данного уклона) — получают точку С. Прямая, проведенная через точки А и С, будет иметь требуемый уклон.

22

Рис. 54

Рис. 55

Рис. 56

5.2. Конусность. Обозначение, построение

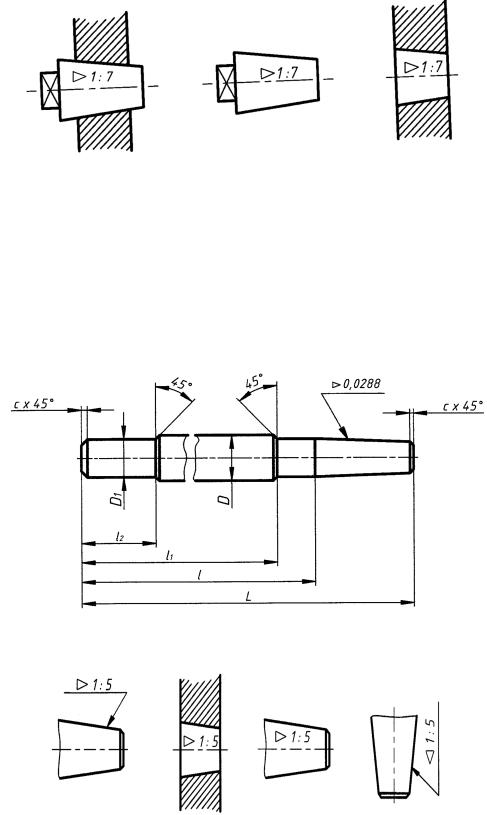
Конус вращения определяется двумя размерами; усеченный конус определяется тремя размерами (рис. 57), задаваемыми в зависимости от условий различным образом: углом α или α/2, одним из диаметров и размером L.

Рис. 57

Конусностью C называется отношение разности диаметров двух поперечных сечений конуса вращения к расстоянию между ними (см. рис. 57). Это отношение равно удвоенному тангенсу половины угла при вершине конуса, т. е. конусность равна удвоенному уклону образующей конуса к его оси.

23

Нормальные конусности и углы конусов выбирают из ряда значений, установленных ГОСТ 8593–81 «Нормальные конусности и углы конусов».

В конических соединениях, т. е. в случаях, когда конический стержень вставляют в коническое отверстие, конусность указывают обязательно (рис. 58).

Рис. 58

Конусность может быть задана отношением двух чисел (см. рис. 58) или десятичной дробью (рис. 59). Знак конусности , острый угол которого должен быть направлен в сторону вершины конуса, наносят перед размерным числом, располагая в зависимости от положения оси конуса так, как показано на рис. 60.

Определение конусности по чертежу и проведение наклонных линий — образующих конуса — согласно данному числовому значению конусности аналогично определению уклонов и проведению прямых заданного уклона.

Рис. 59

Рис. 60

24

6. ЛЕКАЛЬНЫЕ КРИВЫЕ

Все множество плоских кривых можно подразделить на лекальные и циркульные кривые. Лекальную кривую можно рассматривать как линию, состоящую из бесчисленного количества бесконечно малых дуг окружностей при постепенном изменении места их центров и радиусов кривизны. К лекальным кривым относятся кривые второго порядка, спирали, циклические кривые и др.

Среди лекальных кривых наибольший интерес представляют кривые второго порядка: эллипс, парабола и гипербола.

Эти плоские кривые линии можно получить как линии пересечения прямого кругового конуса с плоскостями, различно расположенными по отношению к оси конуса, поэтому эти кривые называют кривыми конических сечений (рис. 61).

Рис. 61

Если угол наклона секущей плоскости к оси конической поверхности равен углу наклона прямолинейной образующей к этой оси, в сечении получается парабола. Если угол наклона секущей плоскости к оси конической поверхности меньше угла наклона образующей конической поверхности к этой оси, секущая плоскость пересечет поверхность по гиперболе. Если угол наклона секущей плоскости к оси конической поверхности больше угла наклона образующей конической поверхности к этой оси, секущая плоскость пересечет поверхность по эллипсу.

6.1. Эллипс

Эллипсом называется плоская замкнутая кривая — геометрическое множество точек, сумма расстояний от которых до заданных точек F1 и F2 равна длине заданного отрезка AB, проведенного через точки F1 и F2 так, чтобы отрезок AF1 был равен отрезку F2B (рис. 62).

В то же время, эллипс есть равномерно сжатая к своему диаметру окружность, все точки которой приближаются к выбранному диаметру так, что расстояния до диаметра уменьшаются в одно и то же число раз. Отрезок AB называется большой осью эллипса, а точки F1 и F2 — фокусами эллипса. Отрезок CD, проведенный через середину большой оси (центр эллипса O) перпендикулярно к ней, называется малой осью эллипса. Биссектриса угла F1KF2 называется нормалью эллипса, а биссектриса смежного с ним угла F2KM — касательной эллипса.

25

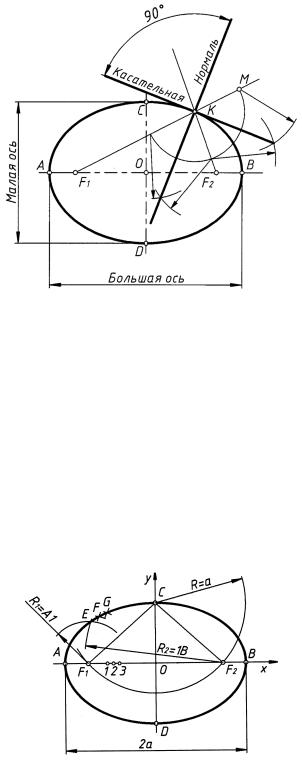
Рис. 62

Способ построения эллипса зависит от того, какие параметры кривой известны. Рассмотрим несколько способов.

Способ 1. Заданы большая ось и фокусное расстояние (рис. 63). На отрезке AB между центром O и одним из фокусов (на рис. 63 — F1) выбирают точки 1, 2, 3 , каждая из которых разделит отрезок AB на две неравные части. Из фокуса F1, как из центра, строят дуги окружностей радиусов A1, A2 и A3, а из фокуса F2 — соответствующие дуги радиусов 1B, 2B и 3B. Пересечение дуг радиусов A1 и 1B дает точку E, пересечение дуг радиусов А2 и 2В — точку F и т. д. На основании свойств симметрии эллипса относительно большой и малой осей достраивают кривую. Точки A, B, C и D пересечения кривой с осями называются вершинами эллипса.

Рис. 63

Способ 2. Если известны большая и малая оси эллипса, то построения выполняют в следующем порядке. На заданных осях эллипса — большой АВ и малой CD — построить как на диаметрах две концентрические окружности (рис. 64). Одну из них разделить на 8—12 равных или неравных частей и через точки деления и центр эллипса O провести радиусы до их пересечения с большой окружностью. Через точки 1, 2, . . . деления большой окружности провести прямые, параллельные малой оси CD,

26

Рис. 64

а через точки 11, 21, . . . деления малой окружности — прямые, параллельные большой оси АВ. Точки пересечения соответствующих прямых принадлежат искомому эллипсу.

Способ 3. Построение эллипса по заданным сопряженным диаметрам (рис. 65). Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряженными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре. Если эллипс является образом окружности при аффинном преобразовании, то его сопряженные диаметры являются образами двух перпендикулярных диаметров этой окружности.

Рис. 65

На данных сопряженных диаметрах АВ и CD построить параллелограмм, стороны которого параллельны диаметрам АВ и CD. Сопряженный диаметр АВ и сторону PQ параллелограмма разделить на произвольное, но одинаковое число равных частей. Из точек C и D провести последовательно пучки лучей через соответствующие точки деления. Пересечения пар лучей, проведенных через одноименные точки деления, определяют точки эллипса (например, луч С2, пересекаясь с лучом D2, образует точку S эллипса). Построение нижней части эллипса аналогично. Отметим, что заданные диаметры AB и CD не являются осями эллипса. Для построения осей MN и KL необходимо пересечь линию эллипса окружностью произвольного радиуса с центром в точке О и точки пересечения Е и F соединить хордой EF. Серединный перпендикуляр к EF определяет положение малой оси KL эллипса; MN KL.

27

Рис. 66

Пример чертежа детали (эксцентрика), имеющей очертания эллипса, показан на рис. 66.

6.2. Парабола

Параболой (рис. 67) называется плоская разомкнутая кривая — геометрическое множество точек, одинаково удаленных от данных точки F и прямой MN (не проходящей через точку F). Точка F называется фокусом, а прямая MN — директрисой (направляющей) параболы; прямая BE, проведенная через фокус перпендикулярно директрисе, называется осью параболы; точка A, лежащая на середине отрезка BF (оси параболы), заключенного между фокусом F и направляющей MN, называется вершиной параболы. Отрезок, соединяющий любую точку C параболы с ее фокусом F, называется радиус-вектором параболы; биссектриса угла FCD, составленного перпендикуляром CD, проведенным из любой точки C параболы к директрисе, и радиус-вектором FC той же точки C, называется касательной в точке C (касательная перпендикулярна отрезку FD); прямая, проведенная через точку C перпендикулярно касательной, называется

нормалью.

Рис. 67

Способ построения параболы зависит от заданных параметров.

Способ 1. Построение по заданным директрисе и положению фокуса F (рис. 68). Вершина параболы находится в точке A на расстоянии ОА = OF/2. Другие точки кривой определяются пересечением прямых, проведенных из произвольных точек 1, 2, . . . параллельно директрисе, с дугами окружностей, центр которых расположен в фокусе F, а радиус равен расстоянию соответствующих точек до директрисы.

28

Рис. 68

Cпособ 2. Построение по заданным вершине, оси и одной из точек параболы (рис. 69). Из точек A и B провести взаимно перпендикулярные прямые до пересечения в точке С. Отрезки AC и BC разделить на одинаковое число равных частей. Из вершины A провести лучи в точки деления на отрезке BC, а из точек деления на отрезке АС — прямые, параллельные оси параболы. На пересечении соответствующих прямых отметить точки одной ветви параболы. Точки другой ветви параболы симметричны относительно оси параболы.

Рис. 69

Способ 3. Построение посредством касательных прямых к параболе в заданных осях (рис. 70). Оси параболы, исходящие из начальной точки O, могут располагаться под тупым или острым углом. Заданные оси OА и OВ разделить на одинаковое число равных частей и пронумеровать точки деления. Точки деления с одинаковыми номера-

Рис. 70

29

ми последовательно соединить прямыми линиями. К полученному семейству прямых подобрать с помощью лекала огибающую касательную кривую — параболу.

6.3. Гипербола

Гиперболой называется плоская разомкнутая кривая — геометрическое множество точек, разность расстояний которых от данных точек F1 и F2 равняется заданному отрезку AB. Гипербола имеет две симметричные ветви (рис. 71).

Рис. 71

Прямая, проходящая через точки A и B — вершины гиперболы, называется действительной осью, а середина отрезка AB (точка O) называется центром гиперболы; прямая CD, проведенная через центр гиперболы O перпендикулярно действительной оси AB, называется мнимой осью. Точки F1 и F2, лежащие симметрично (относительно мнимой оси) на действительной оси, называются фокусами гиперболы. Биссектриса MN угла F1QF2 (точка Q произвольная) является касательной к гиперболе в точке Q, а биссектриса смежного угла EQF2 — нормалью.

Касательные к гиперболе, точки касания которых удалены от вершины на бесконечное расстояние, называются асимптотами (TU и GH). Для их построения проводят из вершин A и B прямые, параллельные мнимой оси, до пересечения с полуокружностью, проведенной из центра O радиусом OF1. Через полученные точки S и P и центр O проводят прямые — асимптоты. Если асимптоты взаимно перпендикулярны, то гиперболу называют равнобокой.

В зависимости от заданных параметров гиперболу строят следующими способами. Способ 1. Построение по заданным вершинам A и А1 и фокусам F и F1 гиперболы при AF = A1F1. На оси гиперболы отметить ряд произвольных точек (рис. 72): 1, 2, . . . , 11, 21, . . . Точки гиперболы определяют построением на пересечении дуг, проведенных из фокусов F и F1. Радиусами дуг служат расстояния от точек до вершин гиперболы,

например: R1 = А3; R2 = А13.

Способ 2. Построение по заданной точке М в системе координат Oxy (рис. 73). Через данную точку М провести вспомогательные оси МB и МK, параллельные соответственно осям Ox и Oy. На оси МK выбрать произвольные точки 1, 2, . . . , через которые провести горизонтальные лучи. Из начала координат O провести через те же точки несколько лучей до пересечения со вспомогательной осью MB в точках

30

Рис. 72 Рис. 73

11, 21, . . . Опуская из этих точек перпендикуляры на горизонтальные лучи, проведенные из точек 1, 2, . . . , отметить ряд точек, принадлежащих гиперболе.

Способ 3. Построение по заданной вершине А и точке С гиперболы (рис. 74). Из точки C опустить перпендикуляр к действительной оси АВ гиперболы и построить прямоугольник ABCD. Стороны CB и DС прямоугольника разделить на одинаковое число равных частей. На оси гиперболы отложить отрезок ОА = AB и провести два пучка лучей: из точки О — к точкам деления стороны CB, из точки A — к точкам деления стороны CD. Взаимное пересечение одноименных лучей определяет положение точек гиперболы.

Рис. 74

6.4. Спирали

Спирали — плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или удаляясь от нее.

6.4.1. Спираль Архимеда

Спираль Архимеда — плоская кривая, представляющая собой траекторию точки, движущейся с постоянной скоростью от центра окружности O по радиусу, вращающемуся также с постоянной угловой скоростью (рис. 75).

Точка O называется полюсом спирали; отрезок OA — шагом спирали; отрезок KL — нормалью спирали, а прямая MN, перпендикулярная нормали, называется касательной. Точка K может располагаться в любом месте спирали, а точку L находят путем построения, для чего точку K соединяют прямой с точкой O и в точке O проводят

31

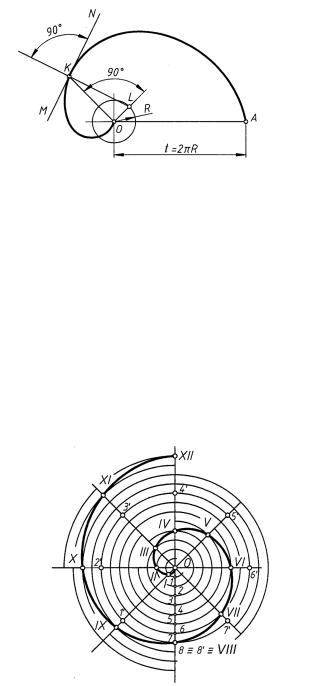
Рис. 75

перпендикуляр к отрезку KO, который пересечет в точке L окружность, проведенную через центр O, радиуса R = t/(2π).

Для построения спирали Архимеда (рис. 76) исходную окружность и ее радиус нужно разделить на одинаковое число равных частей (на рис. 76 n = 8; 1, 2, . . . , 8 — точки деления радиуса; 1 , 2 , . . . , 8 — точки деления окружности). Через точки деления на окружности провести из центра O лучи, последовательно откладывая на каждом из них соответствующее число делений радиуса: на первом луче O1 — расстояние O1, на втором луче O2 — расстояние O2 и т. д. Полученный ряд точек I, II, III, IV, V и т. д. соединить плавной кривой.

Рис. 76

Спираль Архимеда имеет две ветви. Вторая ветвь получается при вращении радиуса окружности против движения часовой стрелки.

На рис. 77 представлен чертеж детали (распределительного кулачка). Очертания его боковых сторон представляют собой спираль Архимеда.

Построение спирали Архимеда на участке между заданными точками представлено на рис. 78. Точки A и B заданы радиусами R1 и R2.

Для построения соединить точки A и B с центром O отрезками OA и OB, на большем радиусе OB отложить отрезок B1 = R2 − R1 и разделить его на произвольное число равных частей (n = 8). На столько же равных частей разделить угол AOB.

32

Рис. 77

Рис. 78

На пересечении лучей, делящих угол, и дуг, проведенных через точки 1, 2, . . . , 8 деления отрезка B1, отметить точки спирали Архимеда.

6.4.2. Синусоида

Синусоидой называется кривая, изображающая постепенное изменение тригонометрической функции — синуса — в зависимости от постепенного изменения величины угла (рис. 79). Прямая А0А12 называется осью синусоиды; точки А3 и A9 — вершинами синусоиды; точки А0, A6 и А12 — точками перегиба; L — длина волны, равная А0А12 (если L = πD, синусоида называется нормальной; если L > πD — вытянутой; если L < πD — сжатой). Величина D называется амплитудой синусоиды.

Рис. 79

Для построения синусоиды проводят вспомогательную окружность диаметром, равным данной амплитуде D, и на продолжении центровой линии отмечают отрезок L, равный заданной длине волны (рис. 80). Окружность делят на некоторое количество, например на 12, равных частей.

Отрезок L делят на столько же равных частей, на сколько была разделена окружность (рис. 81); из точек деления окружности проводят прямые параллельно оси сину-

33

Рис. 80

Рис. 81

соиды, а из точек I, II, III, IV и V — перпендикуляры к оси до пересечения с соответствующими прямыми — получают точки А1, А2, А3, А4, А5.

Аналогичным путем находят точки А7, А8, А9, А10, А11 (точки А, А6 и А12 лежат на оси), через полученные точки проводят кривую, которая явится искомой синусоидой (рис. 82).

Рис. 82

Вид синусоид имеют многие кривые, изображающие гармонические колебательные процессы или являющиеся проекциями винтовых линий.

6.5. Циклические кривые

Циклическими называются кривые, образование которых связано с движением круга, к ним относятся циклоида, эпициклоида, гипоциклоида и др.

6.5.1. Циклоида

Циклоидой называется плоская кривая, представляющая собой траекторию движения точки, принадлежащей окружности S радиуса R, перекатываемой без проскальзывания по прямой линии. Окружность S называется производящей окружностью, а прямая MN — направляющей прямой (рис. 83). Прямая EF называется касательной к циклоиде в точке K; ее проводят через точку K и верхнюю точку вертикального диаметра производящей окружности S1. Прямая GK называется нормалью циклоиды;

34

Рис. 83

ее проводят через точку K и нижнюю точку вертикального диаметра производящей окружности S1. Нормаль перпендикулярна касательной.

Для построения циклоиды (рис. 84) необходимо от начальной точки A окружности провести направляющую прямую и отложить на ней отрезок AA1, равный длине данной окружности: 2πR. Окружность и отрезок AA1 делят на одинаковое число равных частей (n = 12). Восстанавливая перпендикуляры из точек деления прямой AA1 до пересечения с прямой, проходящей через центр данной окружности параллельно AA1, отмечают ряд последовательных положений центра перекатываемой окружности O1, O2, . . . , O12.

Рис. 84

Описывая из этих центров дуги радиуса R, отмечают точки пересечения с ними прямых, проходящих параллельно отрезку AA1, через точки деления окружности 1, 2, 3 и т. д.

На пересечении горизонтальной прямой, проходящей через точку 1, с дугой, описанной из центра O1, находится одна из точек циклоиды; на пересечении горизонтальной прямой, проходящей через точку 2, с дугой, проведенной из центра O2, находится другая точка циклоиды и т. д.

6.5.2. Эпициклоида

Эпициклоидой называется плоская кривая, представляющая собой траекторию движения точки, принадлежащей окружности S радиуса r, катящейся по внешней стороне дуги радиуса R (рис. 85). Окружность S называется производящей окружностью; дуга MN называется направляющей дугой; прямая EF, проведенная через заданную точку K эпициклоиды и верхний конец E диаметра EG производящей окружности S1, имеющего радиальное направление (O0E), называется касательной к эпициклоиде.

35

Рис. 85

Прямая GK, проходящая через точку K и нижний конец диаметра, называется нормалью эпициклоиды.

Для построения эпициклоиды производящую окружность и направляющую дугу делят на 12 частей; проводят из всех точек деления окружности концентрические дуги, центром которых является точка O0 (рис. 86).

Рис. 86

Находят точки пересечения лучей, выходящих из точки O0, с окружностью с центром в точке O0 радиуса R + r, отмечают ряд последовательных положений центра перекатываемой окружности O1, O2, . . . , O12.

Описывая из этих центров дуги радиуса r, отмечают точки пересечения с ними концентрических окружностей, проходящих через точки деления окружности 1, 2, 3 и т. д.

На пересечении концентрической окружности, проходящей через точку 1, с дугой, описанной из центра O1, находится одна из точек эпициклоиды; на пересечении концентрической окружности, проходящей через точку 2, с дугой, проведенной из центра O2, находится другая точка эпициклоиды и т. д.

Длина дуги направляющей окружности определяется центральным углом α = 360r/R. В качестве примера эпициклоиды можно указать на часть кривой профиля зуба

некоторых зубчатых колес.

36

Рис. 87

Эпициклоида, построенная при условии R = r, называется кардиоидой (рис. 87). Для любого луча, выходящего из точки 5 (см. рис. 87), справедливо равенство

12 = 1121 = 13 = 1131 = . . . = 2r. На этом основан простой способ построения кардиоиды: через точку 5 проводят лучи и на них от точек пересечения лучей с направляющей окружностью откладывают по обе стороны отрезки одинаковой длины, равные 2r.

6.5.3. Гипоциклоида

Гипоциклоидой называется плоская кривая, представляющая собой траекторию движения точки, принадлежащей окружности S радиуса r, катящейся по внутренней стороне дуги радиуса R (рис. 88). Окружность S называется производящей окружностью, дуга MN называется направляющей дугой.

Рис. 88

Прямая EF, проведенная через заданную точку K гипоциклоиды и нижний конец E диаметра EG производящей окружности S1, имеющего радиальное направление (O0E), называется касательной к гипоциклоиде. Прямая KG, проходящая через точку K и верхний конец диаметра EG, называется нормалью гипоциклоиды.

Построение гипоциклоиды (рис. 89) аналогично построению эпициклоиды при условии, что положение центров перекатываемой окружности O1, O2, . . . , O12 находят на пересечении лучей, выходящих из точки O0, с окружностью с центром в точке O0 радиуса R − r.

Гипоциклоида, полученная при условии R = 4r, называется астроидой (рис. 90). Наиболее простой приближенный способ построения астроиды основан на том, что эта кривая является огибающей для промежуточных положений отрезка, имеющего длину, равную радиусу направляющей окружности, концы которого скользят по сторонам прямого центрального угла. Для построения одной из арок астроиды необходимо

37