3.2. Отношения на множествах и графы

Каждый ориентированный граф G(X) определяет некоторое от­ношение на множествеXсвоих вершин. Это отношение может быть записано какx_i Gx_j. Оно означает, что в графе есть дуга, идущая отx_iкx_j.

Отношению со свойством рефлексивности(xRх) должна со­ответствовать на графепетля в вершине. Если это отношение со­блюдается во всех вершинах хX, то соответствующий графG(X) должен иметь петлю в каждой своей вершине.

В случае антиреф­лексивногоотношения на мно­жествеX, соответствующий граф ни в одной из вершин не имеет петли.

Симметрическомуотношению на множествеXсоответствует граф снеориентированными ребрами и, наоборот, граф с неориенти­рованными ребрами определяет некоторое симметрическое отношение.

В случае антисимметрическогоотношения на графе невоз­можно присутствие двух дуг (x_i,x_j), (x_j,x_i) на графе, то есть сущест­вование неориентированного ребра. Кроме того, на этих графах нет петель, то есть соответствующее антисимметрическое отношение антирефлексивно.

Отношение, обладающее свойствомтождественности, соот­ветствует графу с антисимметричным отношением на множестве вершин (ориентированному графу) и добавлением петли в каждой вершине. Этот граф не должен иметь контуров.

Рис. 3.18. Свойство транзи­тивности на графе

Граф, соответствующий транзитивномуотношению (рис. 3.18), обладает следующи­ми свойствами: для любой пары ориентированных ребер (дуг) графа (x_i,x_j), (x_j,x_k) имеется за­мыкающая дуга (x_i,x_k). Можно сказать, что в графе, который соответствует транзитивному отношению, для каждого путиS(x_i,x_k) имеется дуга (x_i,x_k) (рис.3.19).

а) б)

Рис. 3.19. Транзитивный (а) и нетранзитивный (б) графы

Отношение, обладающее свойством полноты, опреде­лено на множестве вершин полного ориентированного графа.

Нулевоеотношение определено на множестве вершин ноль-графа.

Универсальноеотношение определено на множестве вершин полного неориентированного графа с петлями.ДополнительноекRотношениеRопределено на множестве вершин дополнительного графаG_d(Х) кG(X).

Графы, соответствующие отношению эквива­лент­ности, пред­ставляют собой совокупность компонент связности (для каждого класса эквивалентности своя компонента) несвязного графа. Каждая компонента несвязного графа должна быть полным неориентиро­ванным графом с петлями (рис. 3.20).

Рис. 3.20. Граф, соответствующий отношению эквивалентности

3.3. Матрицы смежности и инциденций графа

Если в графе G(X) через а_ijобозначить число дуг, идущих изx_i вx_j, то матрицаA= || а_ij || (i= 1, ...,n;j=1, ...,n; гдеn– число вершин графа) называетсяматри­цей смежности вершин графа.

Наличие нулевого элемента на главной диагонали означает от­сутствие петли в соответствующей вершине.

Матрица А^тсоответствует графуG^-1(X). Матрица А является симметрической тогда и только тогда, когда графG(X) – симметри­ческий. Матрица А антисимметрична тогда и только тогда, когда графG(X) – антисим­мет­рический. Матрица А полна тогда и только тогда, когда графG(X) – полный (а_ij+ а_ji1).

Рис. 3.21. Пример графа для определения матрицы

смежности A

Матрицей смежности ребер графа называется такая матрица В = || b_ij|| (I= 1, ...,m;j= 1, ...,m; гдеm- число ребер графа), что:

1

b_ij =

, если ребраg_i и g_j имеют общий конец,

0 в противном случае.

Пусть g₁, ..., g_m – дуги, х₁, ..., х_n – вершины ориентиро­ванного графа G(X). Матрица S = || s_ij || (I = 1, ..., n – номер вершины графа, j = 1, ..., m – номер дуги графа), такая что:

s_ij =

1, если g_j исходит из х_i,

-1, если g_j заходит в х_i,

0, если g_j не инцидентна х_i

называется матрицей инциденций для дуг графа.

Для неорграфа матрица R = || r_ij || размером n х m, где:

1

r_ij =

, если х_i (i = 1, ..., n) инцидентна g_j (j = 1, ..., m),

0 в противном случае

н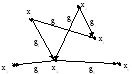азываетсяматрицей инциденций для ребер графа.

Рис. 3.22. Пример графа для определения матрицS и R