ЛПЗ 11

ЛАБОРАТОРНО-ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №11

РАСЧЕТ ФЕРМ

Теоретические основы

Фермой называется геометрически неизменяемая система прямолинейных стержней, соединенных на концах шарнирами.

Места соединения стержней фермы называют узлами.

Для статически определимых ферм имеет место зависимость:

	k = 2n − 3 ,	(1)
где k –	число стержней;
n –	число узлов.

Расчет ферм заключается в решении двух задач:

1.Определение реакций опор.

2.Определение усилий в стержнях.

1. Определение реакций опор фермы. Рассматривается рав-

новесие фермы целиком; составляются уравнения равновесия во

второй ил третьей форме.
Вторая форма условий равновесия:
∑ X k = 0 , ∑mA (Fk ) = 0 , ∑mB (Fk ) = 0 ,	(2)
где ∑ X k и – сумма проекций всех сил на координатную ось x;

∑ mA (Fk ) и ∑ mB (Fk ) – суммы моментов всех сил относительно

любых двух центров A и B соответственно, причем ось x и прямая AB не должны быть взаимно перпендикулярны.

Третья форма условий равновесия (уравнения трех моментов):

∑mA (Fk ) = 0 , ∑mB (Fk ) = 0 ,	∑mC (Fk ) = 0 , (3)
где ∑ mA (Fk ), ∑ mB (Fk ) и ∑ mC (Fk ) –	соответственно суммы

моментов всех сил относительно любых трех центров A, B и C, не лежащих на одной прямой.

2. Определение усилий в стержнях. Делаются следующие до-

пущения:

∙все внешние нагрузки к ферме прикладываются только в узлах;

∙стержни – прямолинейные, невесомые, абсолютно твердые;

∙узлы – идеальные шарниры без трения.

1

Тогда можно полагать, что каждый стержень фермы растянут (усилие в стержне имеет знак «плюс») или сжат (знак «минус»).

Для определения усилий в стержнях применяют следующие методы:

1)Метод вырезания узлов заключается в том, что последовательно мысленно вырезают узлы фермы и рассматривают их равновесие.

2)Метод сечений (метод Риттера) заключается в том, что мысленно рассекают ферму по трем стержням, усилия в которых неизвестны, и рассматривают равновесие той части фермы, на которую действуют меньше сил. Для полученной плоской произвольной системы сил составляют уравнения равновесия, как правило, во второй или третьей форме, т.е. в виде уравнений (2) или (3).

3)Построение диаграммы Максвелла-Кремоны по сути яв-

ляется методом вырезания узлов в графической форме.

Если усилие в отдельном стержне фермы равно нулю, то такой стержень называется нулевым.

Для определения усилий в некоторых стержнях используют

леммы1 о нулевых стержнях:

Лемма 1. Если в ненагруженном узле сходятся под углом два стержня, то усилия в этих стержнях равны нулю.

Лемма 2. Если в ненагруженном узле сходятся три стержня, два из которых на одной прямой, то усилия в этих стержнях равны, а в третьем – равно нулю.

Лемма 3. Если в нагруженном узле сходятся два стержня, а линия нагрузки совпадает с осью одного из стержней, то усилие в этом стержне равно нагрузке, а во втором – нулю.

Также можно пользоваться следующими свойствами:

∙Если в нагруженном узле сходятся три стержня, два из которых на одной прямой, а линия нагрузки совпадает с осью третьего, то усилие в третьем равно нагрузке, а усилия в первых двух равны между собой.

∙Если в ненагруженном узле сходятся четыре стержня, образуя две пересекающиеся прямые, то усилия в стержнях попарно равны.

Рассмотрим вышеперечисленные методы подробнее на кон-

1 Леммой называется доказанное утверждение, полезное не само по себе, а для доказательства других утверждений.

2

кретном примере.

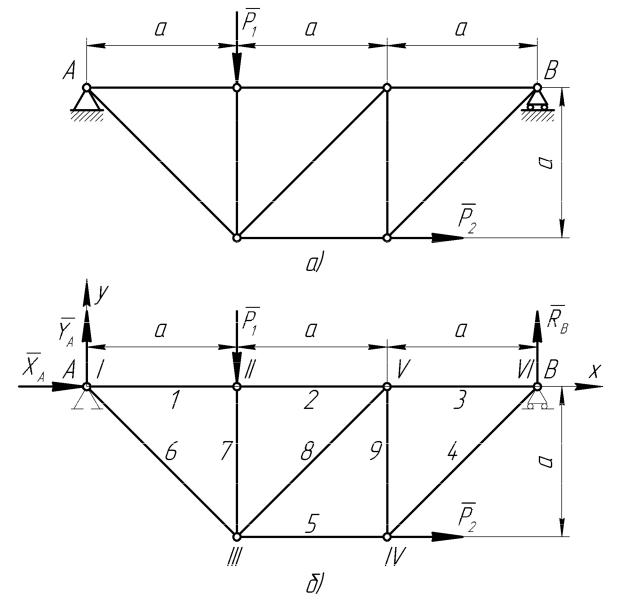
Пример. Определить реакции опор и усилия в стержнях фермы (рисунок 1, а). Ферма нагружена вертикальной силой P1 = 4 кН и горизонтальной силой P2 = 1 кН . Размеры указаны на чертеже.

Решение:

Число стержней фермы k = 9 (рисунок 1, б; стержни пронумерованы арабскими цифрами), число узлов – n = 6 (узлы пронумерованы римскими цифрами). Подставляя эти значения в формулу (1),

рассчитаем ферму на статическую определимость:

9 = 2 × 6 - 3 .

Т.к. равенство верно, то ферма не имеет лишних стержней и, соответственно, статически определима.

Рисунок 1

3

1. Определение реакций опор. Рассмотрим равновесие всей

фермы (рисунок 1, б), покажем силы P1 , P2 и опорные реакции X A ,

YA , RB . В результате получим плоскую произвольную систему сил,

для которой составим уравнения равновесия:

∑ X k = X A + P2 = 0 , ∑Yk = YA − P1 + RB = 0 ,

∑mA (Fk ) = P2 × a - P1 × a + RB × 3a = 0 .

Решая систему уравнений, найдем реакции опор фермы:

X A = − P2 = −1 кН ,

RB = P1 - P2 = 4 - 1 = 1 кН ,

3 3

YA = P1 − RB = 4 − 1 = 3 кН .

2. Метод вырезания узлов. Ферма находится в равновесии, следовательно, каждый узел фермы также находится в равновесии.

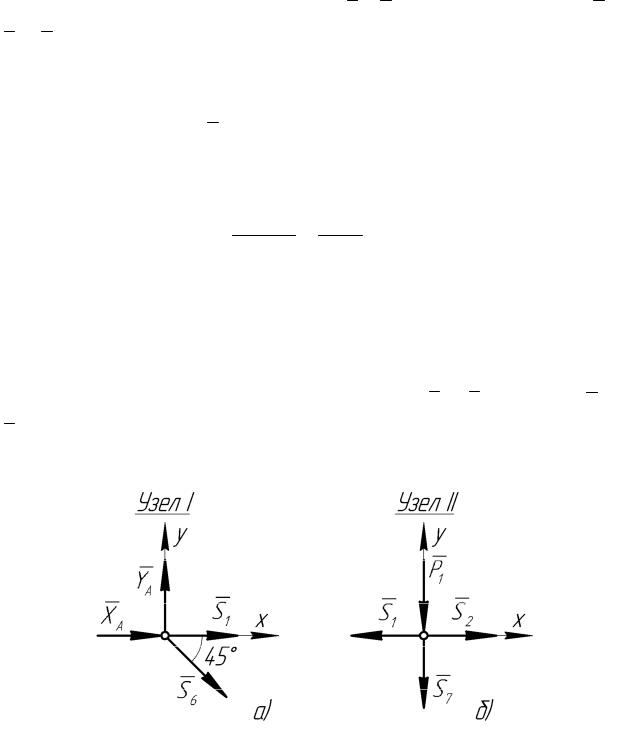
Расчет начнем с узла, в котором сходятся не более двух стержней – с узла I. Мысленно вырежем узел и рассмотрим его равновесие (рисунок 2, а). В нем приложены реакции X A , YA и усилия S1 и

S6 в стержнях 1 и 6 (предполагая, что стержни растянуты, усилия направляем от узла).

Рисунок 2

Выбираем координатные оси и для полученной плоской системы сходящихся сил составляем уравнения равновесия:

∑ X k = X A + S1 + S6 cos 45° = 0 , ∑Yk = YA − S6 sin 45° = 0 .

Решая систему, найдем усилия в стержнях 1 и 6:

4

YA

3

S6

=

=

= 3 2

= 4, 24 кН ,

sin 45°

2 2

S1	= - X A	- S6 cos 45° = 1 - 3 2 ×	2	= -2 кН .
		2

Далее рассмотрим равновесие узла, в котором сходятся два стержня, усилия в которых неизвестны, – узел II (рисунок 2, б). Его

уравнения равновесия:

∑ X k = S2 − S1 = 0 , ∑Yk = − P1 − S7 = 0 ,

откуда усилия в стержнях 2 и 7:

S2 = S1 = −2 кН , S7 = − P1 = −4 кН .

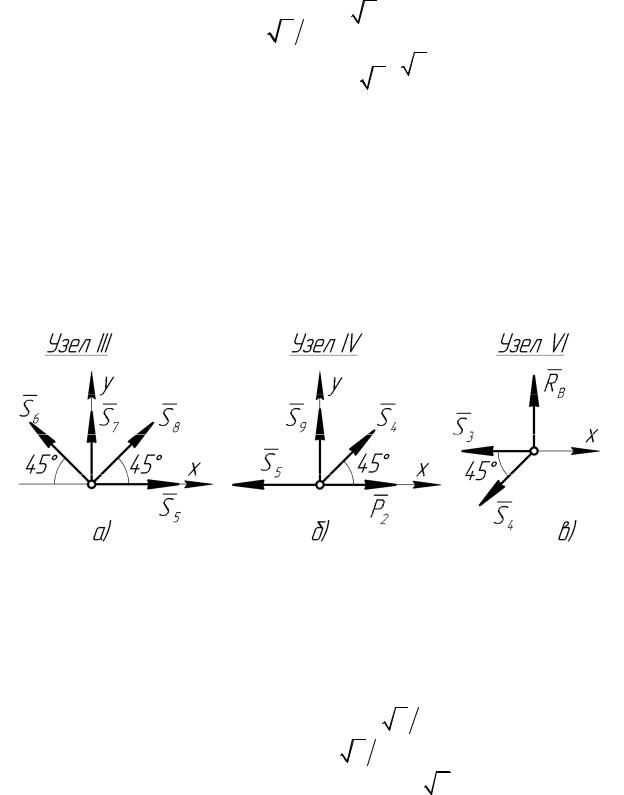
Затем последовательно рассмотрим равновесие узлов III (рисунок 3, а), IV (рисунок 3, б) и VI (рисунок 3, в).

Рисунок 3

Уравнения равновесия узла III:

∑X k = S5 + S8 cos 45° − S6 cos 45° = 0 ,

∑Yk = S7 + S6 sin 45° + S8 sin 45° = 0 ,

откуда усилия в стержнях 5 и 8:

		-S7 - S6 sin 45°			- 4, 24 ×
S8	=		=	4				2 2		= 1, 41 кН ,
		sin 45°
					2 2

S5 = ( S6 - S8 ) × cos 45° = (4, 24 - 1, 41) × 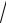2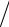2 = 2 кН .

Уравнения равновесия узла IV:

∑ X k = P2 + S4 cos 45° − S5 = 0 , ∑Yk = S9 + S4 sin 45° = 0 ,

откуда усилия в стержнях 4 и 9:

5

S4	=	S5 - P2	=	2	- 1		= 1, 41 кН ,
		cos 45°
			2 2

S9 = - S4 sin 45° = -1, 41 × 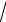2 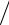2 = -1 кН .

Для узла VI достаточно составить одно уравнение равновесия:

∑ X k = - S3 - S4 cos 45° = 0 ,

чтобы найти усилие в стержне 3:

S3 = - S4 cos 45° = -1, 41 × 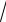2 2 = -1 кН .

Составим таблицу усилий в стержнях и занесем полученные данные (таблица 1).

В результате расчетов усилия в стержнях 1, 2, 3, 7 и 9 получились отрицательными. Это значит, что эти стержни сжаты.

Таблица 1 –		Таблица усилий в стержнях
№ стержня	1		2	3	4	5		6	7	8	9
Усилие, кН	-2		-2	-1	+1,41	+2		+4,2	-4	+1,41	-1

3. Метод сечений (метод Риттера). Ферма находится в равно-

весии, следовательно, любая ее часть также находится в равновесии.

Узлы фермы обозначим латинскими прописными буквами. Рассечем ферму по линии I − I , так чтобы она пересекала три стержня, усилия в которых неизвестны, – стержни 2, 6 и 7 (рисунок 4, а).

Рассмотрим равновесие левой отсеченной части, т.к. к ней приложено меньше сил. Действие правой части на левую заменим усилиями S2 , S6 и S7 , причем, предполагая, что все стержни растянуты, усилия направляем вдоль стержней от рассматриваемой левой части (рисунок 4, б).

Для полученной плоской произвольной системы сил составим уравнения равновесия в третьей форме:

∑mA (Fk ) = -S7 × a - P1 × a = 0 ,

∑mE (Fk ) = - X A × a -YA × a - S2 × a = 0 ,

∑mC (Fk ) = S6 × a sin 45° -YA × a = 0 .

Сокращая в данной системе уравнений на a, получим:

S7 = − P1 = −4 кН , S2 = − X A − YA = 1 − 3 = −2 кН ,

6

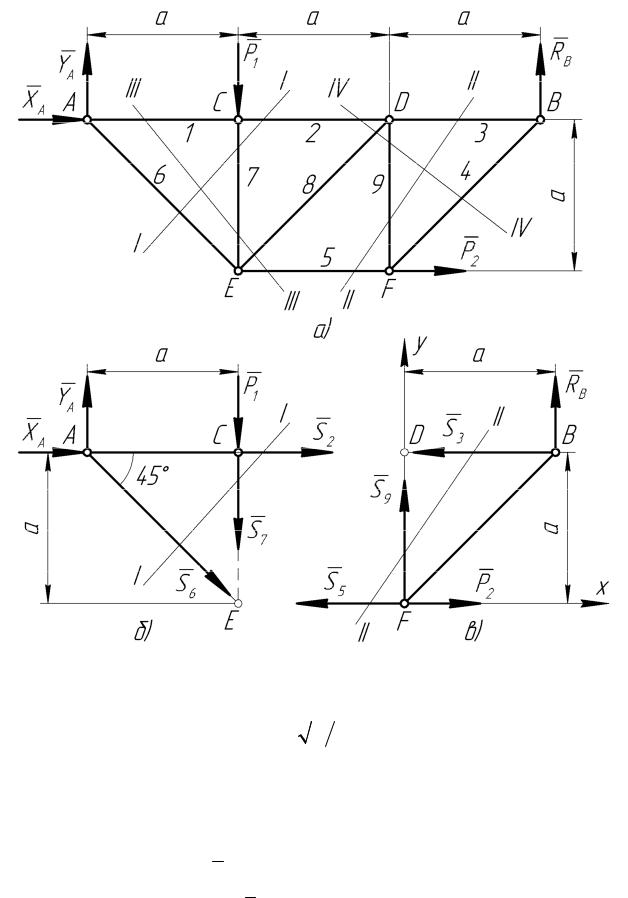
Рисунок 4

	S6	=	YA	=		3		= 4, 24 кН .
			sin 45°
						2 2

Далее рассечем ферму по линии II - II (рисунок 4, а); в этом случае в сечении окажутся стержни 3, 5 и 9. Составим уравнения равновесие для правой отсеченной части (рисунок 4, в):

∑Yk = RB + S9 = 0 ,

∑mD (Fk ) = P2 × a - S5 × a + RB × a = 0 ,

∑mF (Fk ) = S3 × a + RB × a = 0 .

Решая данную систему уравнений, получим:

7

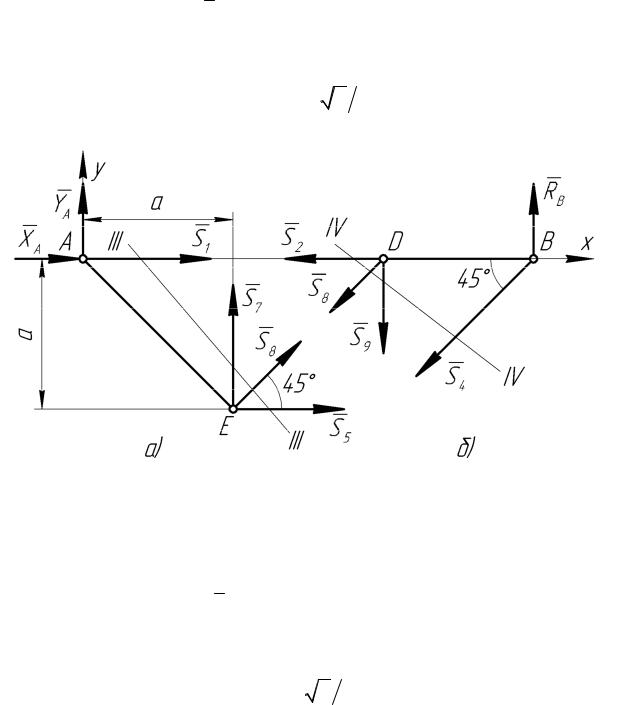
S9 = − RB = −1 кН , S5 = P2 + RB = 1 + 1 = 2 кН ,

S3 = − RB = −1 кН .

Рассечем ферму по линии III - III (рисунок 4, а) и рассмотрим равновесие левой отсеченной части (рисунок 5, а). Для определения двух неизвестных усилий – S1 и S8 – составим два уравнения равновесия:

∑Yk = YA + S7 + S8 sin 45° = 0 ,

∑mE (Fk ) = - X A × a - S1 × a - YA × a = 0 ,

откуда:

S8	= -	YA + S7	= -	3	-	4	= 1, 41 кН
		sin 45°
			2 2

S1 = − X A − YA = 1 − 3 = −2 кН .

Рисунок 5

Для определения S4 рассечем ферму по линии IV − IV

(рисунок 4, а) и составим одно уравнение равновесия для правой отсеченной части (рисунок 5, б):

∑mD (Fk ) = RB × a - S4 × a sin 45° = 0 .

Усилие в стержне 4 составит:

	S4	=	RB	=		1		=1,41 кН .
			sin 45°
						2 2

Анализ найденных усилий в стержнях показывает, что они аналогичны полученным методом вырезания узлов как по модулю, так

8

ипо виду деформации.

4.Построение диаграммы Максвелла-Кремоны.

Предварительно найдем полную реакцию шарнира A:

RA = X A2 + YA2 = 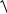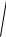(−1)2 + 32 = 3,16 кН .

Также определим направляющие косинусы, а по ним углы

наклона вектора RA к выбранным осям координат (рисунок 6):

cos (

A , x ) =

X A

=

−1

= −0, 316 ,

R

3,16

RA

cos (

, y ) =

YA

=

3

= 0,949 ,

R

A

3,16

RA

( RA , x ) = arccos (−0, 316 ) ≈ 108° , ( RA , y ) = arccos0,949 ≈ 18° .

Рисунок 6

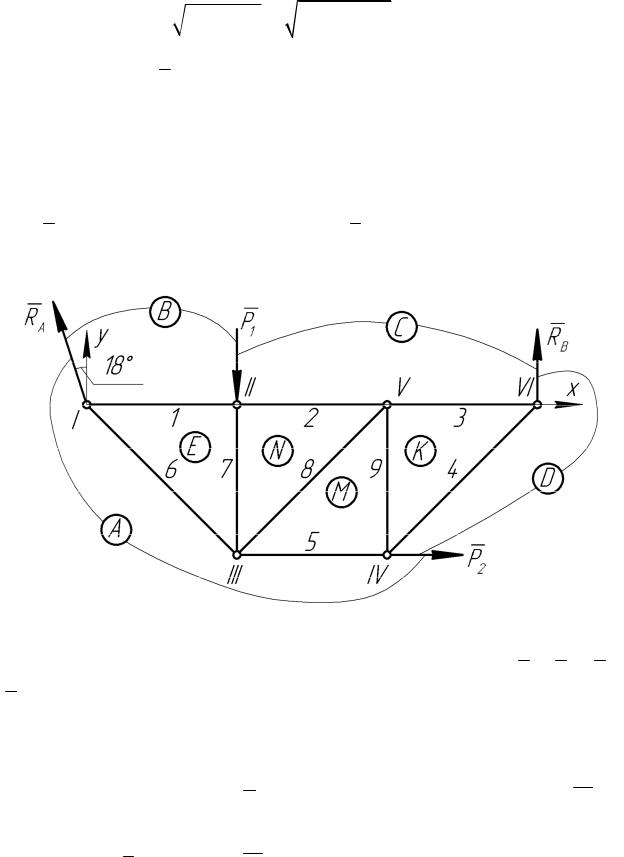
Пространство, лежащее между внешними силами P1 , P2 , RA ,

RB и внешним контуром фермы, разобьем на внешние области –

( A ), ( B ), (C ), ( D ). Пространство, лежащее между стержнями,

разобьем на внутренние области – ( E ), ( N ), ( K ), ( M ) .

Усилие в стержне 1 – S1 – будет соответствовать вектору be на диаграмме, т.к. стержень 1 находится на границе областей ( B ) и ( E ); усилие S2 – вектору cn и т.д.

9

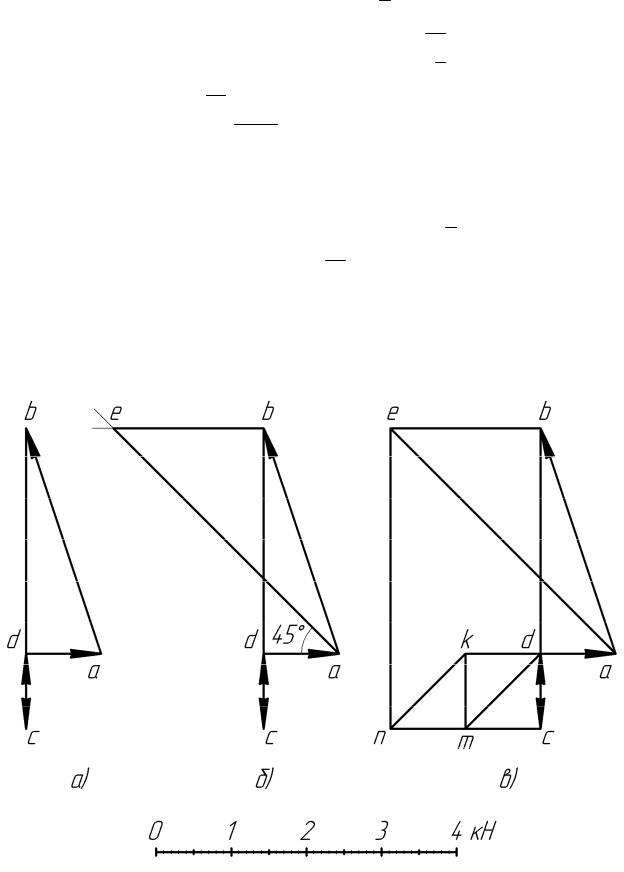
Последовательно обходя внешние области по часовой стрелке, построим многоугольник внешних сил. При переходе из области ( A ) в область ( B ) встречается реакция RA , которую на диаграмме

изображаем в выбранном масштабе вектором ab (рисунок 7, а). Далее, встречая при переходе из ( B ) в (C ) силу P1 , строим в выбран-

ном масштабе вектор bc . Обойдя остальные области в итоге полу-

чим многоугольник abcd , который и будет являться многоугольником внешних сил.

Затем выберем узел, в котором сходятся не более двух стержней – узел I. Обходя этот узел по часовой стрелке, при переходе из области ( A ) в область ( B ) встречаем реакцию RA , которая на диа-

грамме уже изображена вектором ab. На границе областей ( B ) и ( E ) находится горизонтальный стержень 1, усилие в котором неиз-

вестно. Но т.к. усилие направлено вдоль стержня, то на диаграмме проводим из b горизонтальную прямую (рисунок 7, б).

Рисунок 7

10