4.. Случайные величины и их характеристики

Многолетний опыт эксплуатации машин показывает, что продолжительность безотказной работы одинаковых изделий, изготовленных из одной партии сырья и работающих в одинаковых условиях, имеет значительный разброс, а срок службы каждого конкретного изделия невозможно предсказать. Например, рассеяние ресурсов по критерию усталости (оцениваемое отношением наибольшего ресурса к наименьшему) для подшипников достигает 40, для зубчатых передач 10. . .15. Рассеяние ресурсов по износу также весьма значительно. В то же время для большой партии одинаковых изделий можно сделать достаточно определенные выводы о среднем времени безотказной работы, среднем сроке службы, доле изделий, способных проработать безотказно то или иное время, причинах поломок и др. Таким образом, мы оказываемся в ситуации, характерной для теории вероятностей и математической статистики.

Поведение машин и их элементов в эксплуатации зависит не только от условий работы, но и от технологии изготовления. Уже в процессе изготовления закладываются причины различий в свойствах одинаковых машин. Сюда относятся многочисленные отклонения размеров в пределах полей допусков, неоднородная структура металла, различия в свойствах поверхностей трения, неодинаковые величины зазоров и натягов в сопряжениях, усилия затяжки крепежных соединений и т.д. В процессе эксплуатации дополнительное влияние на надежность машин оказывают режимы эксплуатации, дорожные и грунтовые условия, квалификация водителя или оператора, разное качество технического обслуживания и ремонта и т.д. Все это приводит к тому, что изменение параметров каждой машины происходит индивидуально, а появление отказов и предельных состояний носит случайный характер. Поэтому оценить надежность машин и выявить закономерности изменения их параметров можно только статистическими методами[20].

Рассмотрим вначале основные понятия, которые используются в теории вероятностей и математической статистике.

Событие - это всякий факт или явление, происходящее в результате опыта (испытания).

Достоверным называют событие, которое неизбежно произойдет в результате опыта или испытания. Например, замерзание воды при отрицательной температуре; выпадение герба или цифры при бросании монеты.

Невозможным называют событие, которое не может произойти в результате опыта или испытания. Например, замерзание воды при положительной температуре.

Несовместимыми называют два события, если появление одного из них исключает возможность появления другого. Например, отказ и работоспособность - это два события, которые не могут возникать одновременно.

Совместимыми называют два события, если появление одного из них не исключает возможности появления другого. Например, наличие повреждения объекта не исключает появление отказа.

Равно-возможными называют несколько возможных событий, появле­ние которых в результате испытания одинаково возможно.

Независимыми считают такие события, появление которых не зависит от того, какое событие произошло перед этим (например, появление независимого отказа).

Случайным называют событие (явление), которое при рассматриваемом сочетании условий может произойти, а может и не произойти (которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по иному).

Например

1 Стрельба при постоянных условиях

2 Бросание монеты

3 Износ деталей

4 Появление отказов.

При этом основные условия воспроизведения вышеперечисленных опытов будут оставаться неизменными. Неодинаковые результаты ряда опытов будут связаны с наличием каких-то второстепенных факторов, влияющих на исход опыта, но не заданных в числе его основных условий. Таким образом, основные условия опыта, определяющие в общих чертах его протекание, сохраняются неизменными, а второстепенные – меняются от опыта к опыту и вносят случайные различия в его результаты.

Вместе с тем, те факторы, которые относят к «второстепенным» в принципе ничем не отличаются от «основных». Можно было бы точно определить, например, точку попадания снаряда, момент наступления отказа (поломки) детали, траекторию движения автомобиля после столкновения. Но практически такое решение получилось бы необозримо сложным и потеряло бы практическую ценность.

Основные условия можно объединить в процессы, которые описываются функциональными зависимостями, устанавливающими жесткую связь между значением функции и аргументами (например, законы физики, химии, электротехники)

Второстепенные условия можно объединить в случайные (вероятностные) процессы, как правило, являющиеся функцией многих переменных, значения которых имеют определенное рассеивание, а в ряде случаев вообще неизвестны. Например, наработка на отказ автомобиля или агрегата является случайной величиной и зависит от многих факторов:

- первоначального качества материалов деталей;

- точности и чистоты обработки деталей;

- качества сборки;

- качества выполнения ТО и ТР;

- квалификации персонала;

- условий эксплуатации;

- качества применяемых эксплуатационных материалов.

Таким образом, в расчетах надежности многие параметры должны рассматриваться случайными величинами.

Случайной величиной называется величина, которая в результате опыта (испытания) может принимать одно из возможных заранее неизвестных значений. В теории надежности оперируют с такими случайными величинами, как ресурс, наработка до отказа, число отказов за некоторый период эксплуатации, время восстановления и др. Случайные величины могут быть непрерывного или дискретного типа.

Случайная величина называется непрерывной, если она может в результате испытаний принять любое значение в одном или нескольких заданных интервалах. Например, диаметр вала или отверстия в процессе изнашивания, величина зазора или натяга.

Случайная величина называется дискретной, если она может принимать конечное или бесконечное счетное множество значений, то есть если эти значения могут быть пронумерованы в каком-нибудь порядке. К дискретным случайным величинам относятся данные статистических (эмпирических) наблюдений об отказах объектов — на­работка до отказа, число отказов и др.

Проводя какое-либо испытание (опыт, наблюдение) нельзя заранее сказать о значении случайной величины, которое будет получено в результате опыта. Ввиду этого, для количественной оценки случайной величины используется вероятность того, что случайная величина окажется, равна заданному значению или окажется в указанном интервале возможных значений, а также частость (относительное число случаев появления случайной величины в указанном интервале).

Вероятность события - численная мера степени объективной возможности реализации случайного события. События, которые происходят чаще, называются более вероятными; менее вероятными называются события, которые происходят реже; маловероятными - события, которые практически никогда не происходят.

В качестве единицы измерения вероятности принимают вероятность достоверного события, то есть такого события, которое в ре­зультате опыта (испытания) обязательно должно произойти (например, неработоспособное состояние объекта при появлении отказа). Вероятность достоверного события равна единице.

Невозможное событие - это событие, которое в результате опыта (испытания) произойти не может (например, замерзание воды в системе охлаждения при температуре выше 0°С). Вероятность невозможного события равна нулю.

Таким образом, вероятность события изменяется от 0 до I или в общем случае определяется по формуле

Р(А) = m / N , (4.1)

где Р(A) - вероятность появления события А;

m - число случаев, благоприятных событию А (частота события А);

N - общее число случаев.

Однако на практике пользуются не вероятностью события, а относительной частотой, так как вероятность события не всегда возможно вычислить, потому что общее число случаев может быть большим или бесконечно большим. Относительной частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов.

В теории вероятностей доказано, что при неограниченном увеличении числа однородных опытов с практической достоверностью можно утверждать, что относительная частота события будет сколь угодно мало отличаться от его вероятности.

Для полной характеристики случайной величины необходимо задать не только все возможные ее значения, но и закон ее распределения.

Законом распределения называется зависимость, устанавливающая связь между возможными значениями случайной величины и их вероятностями. При расчетах надежности установление закона распределения является необходимой процедурой для получения исходных данных для расчета показателей надежности. При расчетах надежности машин и оборудования в основном используются следующие законы распределения: экспоненциальный, нормальный, Вейбулла.

Закон распределения непрерывной случайной величины задают функцией распределения F(x), которая также называется интегральной функцией распределения. Она определяет вероятность того, что случайная величина X в результате испытания примет значение меньшее х, то есть

F(x) = P(X<x) (4.2)

Функция F(x) является неубывающей функцией х (монотонно возрастающей для непрерывных процессов и ступенчато возрастающей для дискретных процессов). В пределах изменения случайной величины X она изменяется от 0 до 1.

В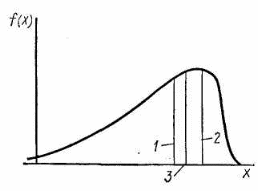теории надежности оперируют временем (наработкой до отказа, ресурсом), то есть некоторой случайной величинойτ, а отказ представляют как событие, состоящее в том, что τ<t. В этом случае функция F(t) наработки τ имеет физический смысл вероятности отказа объекта за время, меньшее t

F(t) = P(τ<t) (4.3)

Производная от функции распределения по текущей переменной (времени t) называется плотностью распределения

f

1 – медиана; 2 – мода;

3 – математическое ожидание

Рисунок 4.1. Плотность вероятности и числовые характеристики центра группирования случайной величины

(t) = dF(t)/dt (4.4)

Она характеризует частость повторений данного значения случайной величины t. В задачах надежности она широко используется как плотность вероятности.

В ряде случаев достаточно характеризовать распределение случайной величины некоторыми числовыми величинами: математическим ожиданием (средним значением); модой и медианой, характеризующими положение центров группирования случайных величин по оси абсцисс; дисперсией, средним квадратическим отклонением, коэффициентом вариации, характеризующими рассеивание случайной величины.

Математическое ожидание (среднее значение) M_t — основная и простейшая характеристика случайной величины t. Значение математического ожидания, определяемое по результатам наблюдений как для дискретных, так и для непрерывных величин, называют оценкой математического ожидания или оценкой среднего значения T,

или , (4.5)

где N — общее число наблюдений;

t_i — значение случайной величины;

g_i — число одинаковых значений t_t.

В первой формуле суммируют все N членов, во второй – число членов с разными значениями t_i. При достаточно большом числе испытаний (наблюдений) полагают, что M_t=T.

В вероятностных задачах математическое ожидание определяют в зависимости от плотности распределения f(t) (для непрерывных величин) или вероятности p_i появления значения t_i (для дискретных величин):

или (4.6)

Дисперсия случайной величины — это математическое ожидание квадрата отклонения этой величины от ее математического ожидания. Оценка дисперсии случайной величины — среднее значение квадрата разности между значениями случайной величины и ее средним значением:

или (4.7)

Для непрерывных случайных величин

(4.8)

Для дискретных случайных величин .

Дисперсия имеет размерность квадрата случайной величины, поэтому пользоваться ею не всегда удобно. Поскольку удобнее пользоваться характеристикой рассеивания случайной величины, имеющей ту же размерность, что и случайная величина, вводится характеристика — среднее квадратическое отклонение

(4.9)

Среднее квадратичное отклонение называют также стандартом, основной ошибкой или основным отклонением. Поскольку среднее квадратичное отклонение имеет размерность случайной величины, пользоваться им удобнее, чем дисперсией.

Для оценки рассеивания с помощью безразмерной (относительной) величины используют коэффициент вариации, равный отношению среднего квадратического отклонения к математическому ожиданию

(4.10)

Введение коэффициента вариации необходимо для сравнения рассеивания величин, имеющих разную размерность. Для этой цели среднее квадратичное отклонение непригодно, так как имеет размерность случайной величины.

Размах рассеивания случайной величины - это разность между максимальным и минимальным ее значениями, полученными в результате испытаний.

R = t_max- t_min (4.11)

При малом числе наблюдений (N <10) размах служит мерой рассеивания.

Квантилем называется значение случайной величины, соответствующее заданной вероятности.

Медианой называется квантиль, соответствующий вероятности 0,5. Медиана характеризует расположение центра группирования случайной величины. Площадь под графиком функции плотности распределения делится медианой пополам.

Модой случайной величины называется ее наиболее вероятное значение, или, иначе, то ее значение, при котором плотность вероятности максимальна. Графически моде соответствует наибольшая ордината.

Для симметричных модальных распределений среднее арифметическое, мода и медиана совпадают.

Параметры надежности используются в статистической трактовке для оценки состояния и в вероятностной трактовке для прогнозирования. Первые выражаются в дискретных числах, их в теории вероятности и математической теории надежности называют оценками. При достаточно большом количестве испытаний они принимаются за истинные характеристики надежности.

Общие зависимости

Существенное рассеяние основных параметров надежности предопределяет необходимость рассматривать ее в вероятностном аспекте.

Как выше было показано на примере характеристик распределений, параметры надежности используются в статистической трактовке для оценки состояния и в вероятностной трактовке для прогнозирования. Первые выражаются в дискретных числах, их в теории вероятностей и математической теории надежности называют оценками. При достаточно большом количестве испытаний они принимаются за истинные характеристики надежности.

Рассмотрим, в качестве примера, проведенные для оценки надежности испытания большой партии одинаковых зубчатых передачN, выходящих из строя вследствие изнашивания зубьев. В начале испытаний и до момента времени t_min все передачи работоспособны. В интервале времени от t_min до t_mах все передачи выходят из строя. При этом в начале количество отказов в единицу времени не велико, затем наблюдается пик отказов, и ближе к t_mах опять спад отказов в виду отсутствия работоспособных передач. Пусть к моменту времени t (t_min < t < t_mах)

останется N_v работоспособных (неотказавших) элементов и п отказавших. Тогда относительное количество отказов Q(t)=n / N.

Если испытание проводится как выборочное, то Q(t) можно рассматривать как статистическую оценку вероятности отказа или, если N достаточно велико, как вероятность отказа.

Вероятность безотказной работы оценивается относительным количеством работоспособных элементов

Т

а – кривая изнашивания зубчатых передач;

б – интегральная функция вероятности

в – функция плотности вероятности

Рисунок 4.2. Определение вероятности отказа и безотказной работы зубчатых передач.

ак как безотказная работа и отказ — взаимно противоположные события, то сумма их вероятностей равна 1:

P(t) + Q(t) = 1 .

Это же следует из приведенных выше зависимостей.

При t = 0 n = 0, Q(0) = 0 и P(t) = 1.

При t = ∞ n = N, Q(t) = 1 и P(t) = 0.

Распределение отказов по времени характеризуется функцией плотности распределения f(t) наработки до отказа. В статистической трактовке , в вероятностной трактовке. ЗдесьΔn и ΔQ (t) — приращение числа отказавших объектов и соответственно вероятности от­казов за время Δt

Вероятности отказов и безотказной работы в функции плотности f(t) выражаются зависимостями

, при t = ∞ ;

.

Интенсивность отказов λ(t) в отличие от плотности распределения относится к числу объектов Nр, оставшихся работоспособными, а не к общему числу объектов. Соответственно в статистической трактовке и в вероятностной трактовке,учитывая, что N_p/N=P(t), ,

Получим выражение для вероятности безотказной работы в зависимости от интенсивности отказов. Для этого в предыдущее выражение подставим , разделим переменные и произведем интегрирование:

; ;

Это соотношение является одним из основных уравнений теории надежности.