Фарковка

	3x1 2x2 x3 5,											3x1 x2 x3 4,
2						x3			1,		7							3x3					17,
	2x1 3x2											2x1 5x2
	2x x			2	3x			3	11			x x			2	x			3	0
		1											1
	x	2x			4x				31,			2x x					x				1,
3	1			2				3	29,		8			1		2				3
	5x1 x2				2x3							x1		x2 x3						6,
	3x x			2	x		3	10				3x x				2	x			3	4
		1												1
	4x		3x			2x				9,		x		5x			x				7,
4		1			2				3		9		1			2				3
	2x1 5x2 3x3 4,											2x1 x2 x3 0,
	5x 6x				2	2x			3	18		x 2x				2	x			3	2
		1											1
	2x x				x			4,				x 2x					3x					6,
5		1		2			3			11,	10		1			2					3		16,
	3x1 4x2					2x3						2x1 3x2						4x3
	3x 2x				2	4x			3	11		3x 2x					2	5x				3	12
		1												1

Задание 1.3.

Решить систему линейных уравнений методом Гаусса.

Вариант

Задание

Вариант

Задание

x1 x2 2x3

3x4

1,

x1 3x2

5x3

7x4

12,

x2

x3

2x4

4,

6x2

2x3

2x4

12,

1

3x1

6

2x1

3x2

x3

x4

6,

5x2 7x3

x4

0,

2x1

3x1

x 2x

2

3x

3

x

4

4

5x 7x

2

x

3

3x

4

4

1

1

x1 2x2 3x3 4x4 5,

x1 2x2 3x3 x4 0,

x2 2x3

3x4 1,

x2 2x3 2x4 2,

2

2x1

7

2x1

2x2 x3

2x4 1,

2x2

4x3 x4 3,

3x1

3x1

4x 3x

2

2x

3

x

4

5

x x

2

x

3

5x

4

2

1

1

x1 3x2

5x3

7x4

12,

x1 2x2

3x3

4x4

11,

5x2

7x3

x4

0,

3x2

4x3

x4

12,

3

3x1

8

2x1

7x2

x3

3x4

4,

4x2

x3 2x4

13,

5x1

3x1

7x x

2

3x

3

5x

4

16

4x x

2

2x

3

3x

4

14

1

1

x1 2x2 x3 x4 8,

x1 x2 2x3 x4 6,

x4

5,

5x2

4x3

3x4 19,

4

2x1 x2 x3

9

2x1

x2 2x3

x4

1,

x2 2x3

3x4

10,

x1

x1

x

x

2

x

3

3x

4

10

4x

6x

2

x

3

2x

4

12

1

1

x1 2x2 x3 x4 8,

x1 2x2 2x3 x4 1,

9,

3x2

x3 3x4

7,

5

2x1 x3 4x4

10

4x1

2x1 x2 x3

x4 5,

2x1 4x2 3x3 4x4 3,

x

x

2

2x

3

x

4

1

2x

2x

2

3x

3

x

4

11

1

1

11

Пример выполнения заданий по теме 1

Задание 1.1. Выполнить действия над матрицами: B·(A + 3B) – A· (A – B), где А

1		2	3		1		3	4
=	2	1	4 ; B =			5	7	8 .
	3	2	3			1	2	4

Решение.

1		3	4	3 1		3 3	3 4	3	9	12
1). 3B = 3·	5	7	8	=	3 5	3 7	3 8	= 15	21 24 .
	1	2			3 1	3 2			6
			4				3 4	3		12

1		2	3	3	9	12	1 3		2 9	3 12	4	11	15
2). A + 3B =	2	1	4	+ 15	21 24		=	2 15	1 21	4 24	= 17	22	28 .
	3	2			6			3 3	2 6
			3	3		12				3 12	6	8 15

1		3	4	4	11	15
3). B·(A + 3B) =	5	7	8	· 17	22	28 =
	1	2			8	15
			4	6

		1 4 3 17 4 6						1 11 3 22 4 8				1 15 3 28 4 15
	=		5 4 7 17 8 6					5 11 7 22 8 8				5 15 7 28 8 15 =
								1 11 2		22 4 8
		1 4 2 17 4 6										1 15 2 28 4 15
		4 51 24					11 66 32			15 84 60			79		109	159
=		20 119 48				55 154 64				75 196 120			= 187		273	391 .
		4	34 24				11 44 32			15 56				62	87
												60				131
1		2	3	1		3	4	1 1		2 3	3 4		0		1	1
4). A – B =	2	1	4	–	5	7	8	=	2 5	1 7	4 8		=	3	6	4 .
	3	2			1	2			3 1	2 2				2
			3				4				3 4				0 1

1		2	3	0		1	1
5). A· (A – B) =	2	1	4	·	3	6	4 =
	3	2			2
			3			0 1

1 0 2 ( 3) 3		2	1 ( 1) 2 ( 6) 3		0	1 ( 1) 2 ( 4) 3				( 1)
=	2 0 1 ( 3) 4	2	2 ( 1) 1 ( 6) 4		0	2 ( 1) 1 ( 4) 4				( 1) =
	3 0 2 ( 3) 3	2	3 ( 1) 2 ( 6) 3 0			3 ( 1) 2 ( 4) 3 ( 1)
		0 6 6		1 12 0		1 8 3	0		13		12
		=	0 3 8	2 6 0		2 4 4	=	5	8		10 .
			0 6 6	3 12 0				0	15		14
						3 8 3

12

		79	109	159	0		13	12
6). B·(A + 3B) – A· (A – B) = 187			273	391 –		5	8	10	=
			87			0	15	14
		62		131
79 0	109 ( 13)	159 ( 12)	79	122	171
= 187 5	273 ( 8)	391 ( 10)	= 182	281	401 .
	87 ( 15)			102	145
62 0		131 ( 14)	62

79		122	171
Ответ: B·(A + 3B) – A· (A – B) = 182		281	401
	62	102	145

5x1 x2 x3 0,
		2x2		3x3		14,
Задание 1.2. Дана система линейных уравнений: x1
4x			3x	2	2x	3	16.
	1

1.Решить систему по формулам Крамера;

2.Решить систему с помощью обратной матрицы.

Решение.

1. Воспользуемся формулами Крамера: x j =			j	, где j = 1; 2; 3.
=	det A, а j– определитель матрицы, получаемой из матрицы системы
заменой столбца j столбцом свободных членов. Тогда
5	1	1
= 1	2 3 = (5·2·2 + 1·3· (– 1) + (– 1) ·3·4) – (4·2·(–1) + 3·3·5 + 1· (–1) ·2) =

4 3 2

= (20 – 3 – 12) – (–8 + 45 – 2) = 5 – 35 = – 30;

0 1 1

1 = 14		2	3			= (0·2·2 + 14·3·(– 1) + (–1)·3·16) – (16·2·(–1) + 0·3·3 + 14 ×
16		3	2
× (–1) ·2) = (0 – 42 – 48) – (–32 + 0 – 28) = –90 – (– 60) = – 30;
		0	1
	5
2 =	1 14 3					= (5·14·2 + 1·16·(– 1) + 0·3·4) – (4·14·(–1) + 5·16·3 + 1·0·2) =
	4	16	2
= (140 – 16 + 0) – (– 56 + 240 + 0) = 124 – 184 = – 60;
		1	0
	5
3 =	1	2	14		= (5·2·16 + 1·3·0 + (–1) ·14·4) – (0· 2·4 + 5·3·14 + 1· (– 1) ·16) =
	4	3	16

13

= (160 + 0 – 56) – (0 + 210 – 16) = 104 – 194 = –90.
Тогда x =	1	30 1,	x		=	2	60			2,		x =		3		90	3.
1		30		2				30					3			30
Ответ: x1	= 1;	x 2 = 2;	x 3	= 3.
								5	1		1
2. Запишем матрицу системы A =								1	2		3		, столбец неизвестных
								4	3		2

x

0

1

X = x

2

, столбец свободных членов B =

14

. Определитель матрицы A равен

x3

16

A

= – 30 0. Тогда решение системы линейных уравнений определяется по

формуле X = A 1 ·B. Для нахождения A 1

воспользуемся формулой: A 1

=

1

A .

A

Для нахождения A cоставим для матрицы A транспонированную матрицу A Ò =

5			1			4
	1		2			3
													и	найдем						элементы союзной матрицы A , как алгебраические
	1 3 2
дополнения элементов матрицы A Ò .
A ij		= (–1) i j M ij .
Тогда: A11 = (–1)1 1 M11																		=					3		= 2·2 – 3·3 = – 5,
																						2
																						3	2
A12 = (–1)1 2 M12														=–			1	3				= – (–1·2 – (–1)·3) = – (– 2 + 3) = – 1,
																	1	2
A1 3 = (–1)1 3 M1 3														=		1		2		= (–1)·3 – (–1)·2 = – 3 + 2 = – 1,
																1		3
A 21		= –					4				= – (1·2 – 3·4) = – (2 – 12) = – (–10) = 10,
						1
						3	2
A 22		=			5		4				= 5·2 – 4·(–1) = 10 + 4 = 14,
				1			2
A 23		= –					1						= – (5·3 – 1·(–1)) = – (15 + 1) = – 16,
						5
						1	3
A 3 1 =						4		= 1·3 – 2·4 = 3 – 8 = –5,
				1
				2		3
A 32		= –								4			= – (5·3 – 4·(–1)) = – (15 + 4) = –19,
						5
						1	3
A 33		=			5		1				= 5·2 – 1·(–1) = 10 + 1 = 11.
				1			2

14

												1				1						1
						5		1	1
												6				30				30
	A-1 =		1	A =	1						=			1				7				8
Тогда							10	14	16																	;
			A		30		5	19				3				15				15
									11			1				19						11
												6				30						30

Cделаем проверку:

												5										1									1
				5			1																																			25 10 5 5														14 19							5 16 11
								1		30										30									30
	-1											10										14							16												1
A A			=	1			2 3																																			5 20							15					1 28 57									1 32 33 =
												30										30							30												30
							3	2																																													4			42				38		4
				4								5								19											11											20 30 10																						48 22
										30										30											30
1		0	0
=	0 1		0 = E.
	0	0
			1
Найдем матрицу Х.
				x										1								1												1											1						0		14				16
																																									0																						1
					1									6								30									30														6								30				30
			Х = x				= А-1В =											1							7									8															1				98				128
					2																																				14		=								0												2 .
														3								15									15														1				3				15				15
				x3										1								19												11							16								0			266					176						3
														6								30												30																		30					30
																																												6
Итак,			решением системы будет x1																										= 1;										x 2 = 2;					x 3					= 3.
Ответ: x1				= 1;			x 2	= 2;		x 3				= 3.

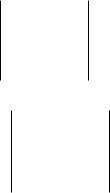
Задание 1.3. Решить систему линейных уравнений методом Гаусса: x 1 + 2x 2 - 3x 3 + x 4 = - 4,

2x1 + x 2 - x 3 - x 4 = 1, x 1 - x 2 + 2x 3 + 3x 4 = 5,

5x1 + 2x 2 - 4x 3 + 2x 4 = - 3.

Решение.

I. Составим расширенную матрицу системы линейных уравнений:

1		2	3	1	4
	2	1	1	1	1
	1	1	2	3	5
	5	2	4	2	3

Первую строку матрицы умножим на -2 и прибавим ко второй строке матрицы, также первую строку умножим на -1 и прибавим к третьей строке и

15

умножив первую строку на -5 прибавим ее к четвертой строке. После этого все элементы первого столбца, кроме первого, окажутся равными нулю.

	1		2	3	1	4		1		2 3		1	4
		2	1	1	1	1			0	3	5	3	9
		1	1 2		3	5			0	3	5	2	9	.
		5	2	4	2	3			0	8	11	3	17

Четвертую строку умножим на -2 и сложим со второй строкой, умноженной на 5 (таким образом, мы получим на месте элемента a 22 единицу).

	1		2 3		1	4		1		2	3	1	4
		0	3	5	3	9			0 1		3	9	11
		0	3	5	2	9			0	3	5	2	9	.
		0	8	11	3	17			0	8	11	3	17

Теперь умножим вторую строку сначала на 3 и сложим с третьей, а затем на 8 и сложим с четвертой.

	1		2 3 1			4		1 2				3	1	4
		0	1	3 9		11			0 1 3				9	11
		0	3 5		2	9			0 0 14				25 42		.
		0	8	11	3	17			0 0			35	75
														105
			Разделим все элементы четвертой строки на 5.
	1		2	3	1	4		1		2		3	1	4
		0	1	3	9	11			0	1	3		9	11
		0	0	14	25	42			0	0		14	25	42	.
		0	0	35	75	105			0	0		7	15	21

Переставим четвертую и третью строки местами.

1		2	3	1	4		1		2	3	1	4
	0	1	3	9	11			0	1	3	9	11
	0	0	14	25	42			0	0	7	15	21
	0	0	7	15	21			0	0	14	25	42

Умножим третью строку на -2 и сложим с четвертой.

1		2	3	1	4		1		2	3	1	4
	0	1	3	9	11			0	1	3	9	11
	0	0	7	15	21			0	0	7	15	21
	0	0	14	25	42			0	0	0	5	0

В результате мы получили треугольную основную матрицу системы линейных уравнений. Запишем соответствующую данной расширенной матрице систему линейных уравнений и решим ее.

II.x1 + 2x 2 - 3x 3 + x 4 = - 4,

x 2 + 3x 3 - 9x 4 = 11, 7x 3 - 15x 4 = 21,

5x 4 = 0.

16

Из последнего уравнения системы находим x 4 = 0. Подставим x 4 = 0 в третье уравнение и найдем x 3 =3. Подставим x 4 = 0 и x 3 = 3 во второе уравнение

системы, получим:	x 2 + 3·3 -	9·0 = 11, из которого находим x 2 = 2.
Подставим x 4 = 0, x 3 = 3, x 2 = 2 в первое уравнение системы, получим:
x1 + 2·2 - 3·3 + 0 = - 4, из которого получаем: x1			= 1.
Проверка. Подставим найденные значения x1 ,			x 2 , x 3 , x 4 в исходную систему
линейных уравнений:
1 + 2·2 – 3·3+ 0 = – 4,		– 4 = – 4 – верно,
2·1 + 2 – 3 – 0 = 1,		1 = 1 – верно,
1 – 2 + 2·3 + 3·0 = 5,		5 = 5 – верно,
5·1 + 2·2 – 4·3 + 2·0 = – 3.		– 3 = – 3 – верно.
Ответ: x1 = 1; x 2	= 2; x 3 = 3,	x 4 = 0.

17

3. Тема 2. Аналитическая геометрия

Краткие теоретические сведения

Уравнения прямой на плоскости:

y = kx + b – уравнение прямой с угловым коэффициентом, Ax + By + D = 0 – общее уравнение прямой,

y - y 0 = k(x - x 0 ) – уравнение прямой, проходящей через данную точку в данном направлении,

	y y1							x x1			– уравнение прямой, проходящей через две точки,
	y	2	y					x	2	x
			1							1
	x			y		1		– уравнение прямой в отрезках,
	a			b

A(x - x 0 ) + B(y - y 0 ) = 0 – уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Вектор n = (A, B), перпендикулярный прямой, называется нормальным вектором этой прямой.

Условие перпендикулярности двух прямых: k2 1 . k1

Условие параллельности двух прямых: k1 k2 .

Расстояние d от точки M 0 (x 0 , y 0 ) до				прямой, заданной уравнением
Ax + By + C= 0 находится по формуле: d =		Ax0 By0 C					.
			A2	B2

Окружностью называется множество точек плоскости, находящим на одном и том же расстоянии от некоторой точки этой же плоскости.

Каноническое уравнение окружности: (x - x 0 ) 2 + (y - y 0 ) 2 = R 2 . M 0 (x 0 , y 0 ) –

центр окружности, R – радиус окружности.

Эллипсом называется множество всех точек плоскости, сумма расстояний от

	каждой из которых до двух данных	точек этой же плоскости, называемых
	фокусами, есть величина постоянная, большая расстояния между фокусами.
	Каноническое уравнение эллипса:	x2			y 2		1.
		a 2
					b2
	Эксцентриситетом эллипса называется								отношение расстояния между
	фокусами к большой оси. Если a > b, то						c		(фокусы лежат на оси абсцисс,
							a

их координаты F1,2 ( c;0) , c2 a2 b2 ); если b > a, то bc (фокусы лежат на

оси ординат, их координаты F1,2 (0; c) , c2 b2 a2 ).

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

18

Канонические

уравнения гиперболы:

x2

y 2

1

(фокусы гиперболы лежат

a2

b2

на

оси

абсцисс,

их

координаты

F

( c;0)

, c2 a2

b2 )

и

x2

y2

1

a2

1,2

b2

(фокусы

гиперболы

лежат на

оси

ординат,

их

координаты

F1,2 (0, c) ,

c2

a2 b2 ).

Эксцентриситетом гиперболы называется отношение расстояния между

фокусами к действительной оси. Если фокусы гиперболы лежат на оси абсцисс,

то ac ; если фокусы гиперболы лежат на оси ординат то bc .

Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Расстояние от фокуса F до директрисы параболы называется параметром параболы, обозначается p, p > 0.

Канонические уравнения параболы:

y2 = 2px (фокус имеет координаты F ( 2p ;0) ); y2 = -2px (фокус имеет координаты F ( 2p ;0) ); x2 = 2py (фокус имеет координаты F (0; 2p ) );

x2 = -2py (фокус имеет координаты F (0; 2p ) ).

Уравнения плоскости в пространстве:

A(x – x 0 ) + B(y – y 0 ) + C(z –z 0 ) = 0 – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору,

Ax+ By + Cz + D = 0 – общее уравнение плоскости,

x x1

y y1

z z1

x2 x1

y2 y1

z2

z1

0 – уравнение плоскости, проходящей через три

x3 x1

y3 y1

z3 z1

данные точки,

x

y

z

1

– уравнение плоскости в отрезках.

a

b

c

Уравнения прямой в пространстве:

x x0

y y0

z z0

- канонические уравнения прямой,

m

n

p

x x1

y y1

z z1

- уравнение прямой, проходящей через две точки,

x

2

x

y

2

y

z

2

z

1

1

1

A1 x+ B1 y + Cz1 + D1 = 0,

19

A 2 x+ B 2 y + C 2 z + D 2 = 0 – общие уравнения прямой.

Угол

между

прямой, заданной в

пространстве

уравнением

x x0

y y0

z z0

и плоскостью, заданной уравнением Ax+ By + Cz + D = 0,

m

n

p

находится по формуле: sin =

Am Bn Cp

.

A2 B2 C 2 m2 n2 p 2

Расстояние d

от точки M 0 (x 0 , y 0 , z 0 )

до плоскости, заданной

уравнением Ax + By + Cz + D= 0 находится по формуле: d =

Ax0

By0 Cz0 d

.

A2 B2 C 2

Задания к расчетно-графической работе

Задание 2.1. Найти длину высоты AD в треугольнике с вершинами А, В, С и написать уравнение перпендикуляра, опущенного из точки С на прямую АВ.

Вариант	А	В	С	Вариант	А	В	С
1	(-3; 4)	(-2; -1)	(-1; -7)	6	(3; 2)	(2;-5)	(-6; -1)
2	(4; -5)	(-3; 3)	(-5; -2)	7	(6; -4)	(-3; -7)	(-1; 2)
3	(3; 5)	(-4; -3)	(2; -4)	8	(-2; -1)	(7; 3)	(4; -3)
4	(-3; -2)	(5; -4)	(1; 6)	9	(3; 4)	(6; 7)	(1; 1)
5	(-2; 5)	(3; 4)	(4; -2)	10	(-4; -5)	(3; -3)	(5; 2)

Задание 2.2. Определить тип кривых и построить их. Для эллипса, гиперболы найти полуоси, эксцентриситет, координаты фокусов; для параболы – параметр р и координаты фокуса, для окружности – координаты центра окружности и радиус окружности.

à) x 2 2 y 3 2 9;

à) x 3 2 y 5 2 4;

á)

x 2

y 2

1;

á)

x 2

y 2

1;

1

25

9

6

49

4

x

2

y

2

x

2

y

2

â)

1;

â)

1;

49

25

25

16

ã)x 2 9 y.

ã) y 2 7x.

à) x 1 2 y 2 2

16;

à) x 3 2 y 4 2

25;

á )

x 2

y 2

1;

á )

x 2

y 2

1;

2

36

25

7

25

16

â)

x 2

y 2

1;

â)

x 2

y 2

1;

16

9

64

25

ã) y 2 5x.

ã) y 2 16x.

20