Фарковка

	b	b
2)	kf (x)dx k f (x)dx;
	a	a
	b	b	b
3)	( f1 (x) f2 (x))dx f1 (x)dx f2 (x)dx
	a	a	a
				b	b
4)	Если f(x) (x) на отрезке [a, b]			то f (x)dx (x)dx
				a	a

5) Если m и M – соответственно наименьшее и наибольшее значения функции

			b
	f(x) на отрезке [a, b], то:	m(b a) f (x)dx M (b a) ;
			a
6)	Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на
			b
	этом отрезке существует точка c такая, что f (x)dx (b a) f (c) .
			a
	Формула Ньютона – Лейбница: Если функция F(x) – какаялибо перво-
			b
образная от непрерывной функции f(x), то			f (x)dx F (b) F (a) .
			a
	Метод интегрирования подстановкой (заменой переменной):
b
		( ) = а,	( ) = b.
f (x)dx f [ (t)] (t)dt , здесь
a
		b			b	b
Метод интегрирования по частям: udv uv						vdu.
		a			a	a

Геометрический смысл определенного интеграла: Определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

Задания к расчетно-графической работе

Задание 5.1. Найдите неопределенные интегралы.

Вариант

Вариант

1

e x dx

6

а)

arcsin x

а)

;

dx ;

1 x2

1 e x

б)

x ln x 1 dx ;

б) 4x cos xdx ;

в)

(x 18)dx

;

в)

(x 4)dx

;

x2 2x 8

x2 4x 12

41

г)

x 2dx

;

г)

xdx

;

x

4

x

д)

sin 4 x cos xdx .

д)

sin x cos 4 xdx .

2

а)

e x dx

;

7

а)

xdx

;

e x 1

x 2 1

б)

xdx

;

б)

x

2

e

x

dx ;

sin

2

x

(x 12)dx

(x 23)dx

в)

;

в)

;

x

2

x

6

x2

x 20

dx

dx

г)

;

г)

;

2

x

1

x

3

д)

sin 5x cos 3xdx .

д) sin x cos 3xdx .

3

а)

x3 dx

;

8

а)

xdx

;

2x2 3

1 x8

б)

2xe

x

dx ;

б)

arctgx

dx ;

x

2

(x 19)dx

в)

;

5xdx

2

x

2x 15

в)

x2

x

6

;

г)

x 2dx

;

г)

x 3dx

;

1

x 2

x

д)

sin3 x cos xdx .

д)

sin x cos

5

xdx .

4

а)

x 2 dx

;

9

а)

e x2 1 xdx ;

x6

1

б)

4x sin xdx ;

б)

xarctgxdx ;

в)

(2x 9)dx

;

(5x 2)dx

в)

;

x

2

5x

6

x

2

2x 8

dx

г)

;

xdx

г)

;

x (x 1)

x 6

д)

sin x cos 7xdx .

д)

sin 7x cos xdx .

5

а)

x sin 1 x2 dx ;

10

а)

x 2 dx

;

б) 5x cos xdx ;

1

x

6

б)

2x 3 sin xdx ;

в)

(11x 2)dx

;

(x 13)dx

x

2

x 2

в)

;

x

2

2x

8

г)

dx

;

dx

x

5

г)

;

1

x

4

д) sin x sin 3xdx .

д)

cos x cos 7xdx .

42

Задание 5.2. Вычислить площадь фигуры, ограниченной линиями.

Вариант		Задание			Вариант	Задание
1	y ex ,	y e x ,		x 1	6	y x2 3x,		y x2 3x
2	3x2 4y 0, 2x 4y 1 0				7	y ex ,	y e x ,		x 2
3	y x2 1,		y x 1		8	y x 1,	y x2 2x 1
4	y x2 4x,		y x 4		9	y ex ,	y e x ,		x 2
5	y2 x 1,		y x2 2x 1		10	y x2 3,		y 2x

Пример выполнения заданий по теме 5

Задание 5.1. Найдите неопределенные интегралы:

а)

sin x cos xdx ;

б) x(x2 1)3 / 2 dx. ;

в)

ln

x

dx ;

3

x

г)

x2 sin xdx ;

д)

(2x 5)dx

;

x

2

2x

3

е)

dx

;

x 1 1

ж) sin 7x sin 2xdx ;

Решение.

а)

Сделаем замену t = sinx, dt = cosxdt. Тогда:

cos xdx =

dt t1/ 2 dt

2

t 3 / 2

C

2

sin 3 / 2 x C.

t

sin x

3

3

б) Выполним замену:

t x2

1; dt 2xdx;

xdx

dt

; Получаем:

2

t

3 / 2

dt

1

t 3 / 2 dt

1

2

t 5 / 2

C

t 5 / 2

C

(x2 1)5 / 2

C;

2

2

2

5

5

5

в) Воспользуемся методом интегрирования по частям:

1

u ln x;

dv

dx;

ln x

x3

ln x

1

1

ln x

1

dx

ln x

dx

(

)

dx

x3

1

1

2x 2

2x

2

x

2x 2

2

x3

2x 2

du

dx;

v

;

x

2x

2

1

1

x 2

ln x

1

C

C.

2x2

4x 2

2

2

43

г) Применим метод интегрирования по частям дважды:

	2	; dv sin xdx;			x2 cos x ( cos x) 2xdx
x2 sin xdx u x
du 2xdx;			v cos x

x2 cos x cos x 2xdx

u 2x;

dv cos xdx;

x2 cos x 2x sin x 2sin xdx x2 cos x 2xsin x 2cos x C.

2dx;

v sin x

du

д)

Представим дробь

2x 5

в виде суммы простейших дробей.

x2 2x 3

Так как

x2 2x 3 (x 3) (x 1),

то

2x 5

=

A

B

.

x2 2x 3

x 3

x 1

Тогда

2x 5

=

A(x 1) B(x 3)

.

Откуда

следует, что 2x + 5 = A(x – 1) +

x2 2x 3

x2 2x 3

+ B(x + 3). Положим x = -3, тогда -1 = -4A, то есть A =

1

; Положим x = 1,

4

1

7

7

2x 5

4

4

тогда 7 = 4B, то есть B =

. Следовательно,

=

. Тогда

4

x2 2x 3

x 3

x 1

1

7

1

7

(2x

5)dx

1

dx

7

dx

4

4

4

4

dx

dx

dx

=

x

2

2x 3

4

x

x

1

x

3 x

1

x 3

x 1

3 4

=

1

ln

x

3

7

ln

x

1

C

4

4

е) Для нахождения данного интеграла воспользуемся подстановкой t =

x 1 .

Тогда

t 2 x 1 , откуда x t 2

1 и dx 2tdt . Таким образом,

dx

2tdt

.

x 1 1

t 1

Так как под знаком интеграла получилась неправильная дробь

2t

,

то

t 1

разложим неправильную дробь на сумму правильной дроби и многочлена.

Выполнив деление числителя на знаменатель, получим:

2t

= 2 -

2

. Тогда

t 1

t 1

2t

2

2

1

dt

2

dt

2dt

dt

2

dt 2

dt 2t 2 ln

t 1

C .

t 1

t 1

t

t

1

1

Сделав обратную замену t =

x 1 , получим, что

dx

2tdt

t

1 = 2

x 1 2ln

x 1 1

C 2 x 1 2ln(

x 1 1) C .

x 1 1

ж) Для нахождения данного интеграла воспользуемся формулой:

44

								sin sin			=		1		(cos( ) cos( )) .
													2
Тогда:
sin 7x sin 2xdx						= =			1	(cos 5x cos 9x)dx =							1		cos 5xdx	1	cos 9xdx	=
							2						2							2
1		1			1		1				1		1
=				sin 5x				sin 9x C						sin 5x				sin 9x C.
	2		5		2		9
												10				18

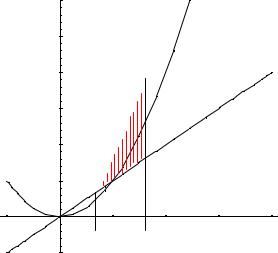
Задание 5.2. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.

Решение.

Построим графики функций: y = x, y = x2, x = 2.

График функции y = x – прямая, являющаяся осью симметрии первого и третьего координатных углов, график функции y = x2 - парабола с вершиной в точке (0;0), а графиком линии x = 2 является прямая, перпендикулярная оси абсцисс и проходящая через точку (2; 0). Искомая площадь фигуры заштрихована на рисунке:

	6
	5
	4
	3
	2
	1
- 1	1	2	3	4
	- 1

Тогда

		2									2						2	x		3	2	x	2		2
S ô	= (x					2	x)dx x						2		dx xdx						|			|
																			3			2
		1									1						1				1				1
	8		1				(2	1	)	7		3				5	(ед2)
	3		3					2		3		2				6

45

7. Тема 6. Дифференциальные уравнения.

Краткие теоретические сведения

Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные (или дифференциалы) различных порядков этой функции.

Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным.

Решением дифференциального уравнения называется такая функция, которая при подстановке ее в это уравнение обращает его в тождество.

Общим решением обыкновенного дифференциального уравнения n-го порядка называется такое его решение y = f(x, c1 , c 2 , …,c n ), которое является

функцией переменной x и n произвольных независимых постоянных c1 , c 2 , …,

c n .

Частным решением обыкновенного дифференциального уравнения называется решение, которое получается из общего решения при некоторых конкретных значениях постоянных c1 , c 2 , …,c n .

Задачей Коши называется нахождение частного решения дифференциального уравнения, удовлетворяющего некоторым начальным условиям.

Дифференциальным уравнением первого порядка называется уравнение вида

F(x, y, y / ) 0 .

Дифференциальное уравнение первого порядка, которое можно

преобразовать к виду P (x) Q (x)dx P (x) Q (x)dy 0 , называется уравнением
1	1	2	2
с разделяющимися переменными.
Дифференциальное уравнение y /		f (x, y)		называется однородным уравне-
нием первого порядка, если функцию		f (x, y)		можно представить как функцию

	y
отношения своих аргументов, то есть	f (x, y)		.
	x

Дифференциальное уравнение первого порядка называется линейным, если его можно преобразовать к виду: y/ p(x) y g(x) .

Дифференциальное уравнение вида y// p y/ qy f (x) называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами.

46

Задания к расчетно-графической работе

Задание 6.1. Решить дифференциальное уравнение первого порядка.

1.

а)

4xdx 3ydy 3x2 ydy 2xy 2 dx ;

6.

а)

x

5 y 2 dx y 4 x2 dy 0 ;

y

2

y

12

б)

y

x ;

y

x

б)

;

x

x

3

в) x 2y dx xdy 0 .

в)

xdy 2y x dx 0 .

2.

7.

а)

y 4 ex dy ex dx 0 ;

а)

4 y 2 dx ydy x2 ydy ;

y

2

б) y 2xy 2x3 ;

б)

y

2x

x ;

в) y

x y

.

dx 2xydy 0 .

в)

x2 y2

x

3.

а) 6xdx 6ydy 2x2 ydy 3xy 2 dx ;

8.

а)

2xdx 2ydy x2 ydy 2xy 2 dx ;

2

3

y

2

б)

y

x y

x ;

б)

y

x

x2 ;

в)

x2

3y2 dx 2xydy 0 .

в) x y dx xdy 0 .

4.

9.

а) x 3 y 2 dx y 2 x2 dy 0 ;

а) x 4 y 2 dx y 1 x2 dy 0 ;

3y

2

y

3

б)

y

x

x3 ;

б)

y

2 x 2x ;

в)

x2

2xy dx xydy 0 .

в) y x dx y x dy 0 .

5.

а)

e2 x 5 dy ye2x dx 0 ;

10.

а)

ex 8 dy ye x dx 0 ;

y

y

1

б)

y

x 3x ;

б)

y

x

x2 ;

в) x y dx y x dy 0 .

в)

xdy

x 2y dx .

Задание 6.2. Решить линейное неоднородное дифференциальное уравнение второго порядка.

1.	y 8y / 17 y 10e2x	6.	y 3y 2y (34 12x) e x
2.	y y 6y (6x 1) e3x	7.	y 6y 10y 51e x
3.	y 2y / 8y 12sin 2x 36cos 2x	8.	y y 2cos x (4x 4) sin x
4.	y 7 y / 12y 3e4 x	9.	y 6y 10y 74e3x
5.	y 2y 6 12x 24x2	10.	y 3y 2y 3cos x 19sin x

47

Пример выполнения заданий по теме 6

Задание 6.1. Решить дифференциальное уравнение первого порядка.

а) 20xdx 3ydy 3x2 ydy 5xy 2 dx ; б) xy y x 1;

y
в) xy y ln	.

x

Решение.

а) Уравнение 20xdx 3ydy 3x2 ydy 5xy 2 dx является уравнением с разделяющимися переменными.

1. Разделим переменные. Перенесем слагаемые с dx в левую часть, а слагаемые с dy в правую: 20xdx 5xy2dx 3x2 ydy 3ydy . Вынесем за скобки общие

множители:

5x(4 y2 )dx 3y(x2 1)dy . Разделим обе части на (4 + y 2 )·(x 2 +

1):

5x

dx

3y

dy .

x2

1

y 2 4

2. Возьмем интегралы от правой и левой частей уравнения, применив метод

5x

3y

подстановки:

dx

dy ,

x2 1

y 2 4

5

5x

dx

t x2 1, dt 2xdx,5xdx

5

dt

2

dt

5

ln

t

1

ln

C

=

x2 1

2

t

2

2

1

5

1

. Аналогично

3y

3

=

ln

x2 1

ln

C1

dy

ln

y2 4

.

2

2

y 2 4

2

3

4

5

1

1

Тогда:

ln

y 2

=

ln

x2

ln

C1

.

2

2

2

3. Выразим y из данного равенства. Для этого умножим данное равенство на 2 и

применив свойства логарифмов,

получим: ln y 2

4 3 ln C2 (x2

1)5 .

Откуда

5

( y2 4)3

C2 (x2 1)5 ;

y2 4 C 3 (x2 1)5 ; y2

C(x2 1) 3 4.

Таким

5

образом,

y =

C(x2 1) 3

4 .

б) Уравнение

xy y x 1 является линейным уравнением.

Разделим обе

части на x. Тогда получим: y' +

y

= 1 +

1

.

x

x

Решим данное уравнение методом Бернулли.

Решение уравнения ищем в виде y = uv, тогда y' = u'v + uv'. Подставим y' и y в

уравнение y' + xy = 1 + 1x y' + xy = 1 + 1x . Тогда получим:

48

u'v + uv' +

vu

= 1 +

1

. Сгруппируем второе и третье слагаемое левой части

x

x

уравнения и вынесем за скобки u, тогда получим u'v + u(v' +

v

) = 1 +

1

.

x

x

1. Найдем

частное

решение

уравнения

v'

+

v

=

0.

Это

уравнение с

x

разделяющимися переменными. Заменим v'

на

dv

и разделим переменные

v и

dx

x:

dv

v

dv

dx

.

Тогда

dv

dx

и

ln

v

ln

x

ln

C1

. Откуда по

v

dx

x

v

x

C1

x

свойствам логарифмов получаем v =

. Возьмем C1 = 1 и получим искомое

x

частное решение: v =

1

.

x

2. Подставим данное частное решение в уравнение u'v + u(v' +

v

) = 1 +

1

.

x

x

Тогда получим u'·

1

= 1 +

1

, которое является уравнением с разделяющимися

x

x

переменными. Найдем общее решение данного уравнения. Так как u' =

du

то

dx

имеем

du

x 1

. Умножим обе части данного уравнения на dx·x, получим du

dx x

x

= (x + 1)dx. Взяв

интегралы от обеих

частей

уравнения: du (x 1)dx ,

получим u =

x 2

+ x + C.

2

1x

= 2x 1 Cx .

+ x + C)·

3. Тогда y = uv = ( x2

2

y

y

y

в) Разделим обе части уравнения

xy y ln

на y, тогда получим

y

ln

,

x

x

x

которое является

однородным

дифференциальным

уравнением

первого

y

y

y

ln

порядка, так как

x

x

x .

Введем новую переменную u =

y

и найдем y' = u'x + u. Подставим y' и

y в

x

y

y

y

уравнение

ln

, которое будет уравнением с разделяющимися

x

x

переменными: u'x + u = u·lnu . Разделим переменные u и x. Так как u' =

du

то

dx

имеем

du x

u ln u u . Умножим обе части уравнения на

dx

. В итоге

dx

x u(ln u 1)

du

dx

получим

.

u (ln u 1)

x

49

Возьмем

интегралы

от

обеих

частей

уравнения.

Так

как

du

t ln u 1, dt

du

dt

ln

t

ln

ln u 1

,

dx

ln

x

ln

C

,

то имеем:

u(ln u 1)

u

t

x

ln

ln u 1

ln

x

ln

C

. Применив свойства логарифмов и учитывая,

что

С –

константа, получим lnu – 1 = Cx, откуда lnu = Cx + 1. Тогда u = e Cx 1 . Так как y = ux, то получаем: y = x·e Cx 1 .

	5		б) y = 2x 1 Cx ;
Ответ: а) y =	C(x2 1) 3	4 ;		в) y = x·e Cx 1 .

Задание 6.2. Решить уравнения:

а) y 2y y 3ex ;

б) y y sin 2x;

в) y y/ x 2;

г) y 7 y 6y (x 2)ex .

Решение.

а) Общее решение данного линейного уравнения второго порядка с постоянными коэффициентами найдем, как сумму общего решения соответствующего однородного уравнения и частного решения исходного неоднородного уравнения: yîí yîî y÷í .

1. Найдем общее решение однородного уравнения y 2y y 0. Для этого составим характеристическое уравнение для данного линейного однородного дифференциального уравнения: k 2 2k 1 0.Найдем корни этого квадратного уравнения: k1 k2 k 1. Так как в случае D = 0 общее решение линейного

однородного дифференциального				второго				порядка с постоянными
коэффициентами имеет вид y		îî	C ekx C			2	xekx ,	то общее решение исходного
			1
уравнения будет иметь вид: y	îî		C ex C		xe x .
			1	2

2. Теперь найдем частное решение исходного дифференциального уравнения

y 2y y 3ex .

Так как f(x) = 3ex ,

то

частное

решение

данного

дифференциального уравнения имеет вид:

y

֒ = y = Ae

x

x

2

1,

0, t

2, l

0) .

(

Для нахождения A воспользуемся методом неопределенных коэффициентов.

y 2Axe x Ax 2ex ;

y 2Ae x 2Axe x 2Axe x Ax 2ex 2Ae x 4Axe x Ax 2ex .

Подставляя в исходное уравнение

y, y/ , y// , получаем:

2Ae x 4Axe x Ax 2ex

4Axe x

2Ax 2ex Ax 2ex

3ex . Откуда

2A 3;

A

3

.

2

Частное решение имеет вид:

y֒

= y

3

x2 e x .

2

3. Тогда общее решение линейного неоднородного уравнения будет иметь вид:

y C1e x C2 xe x 32 x2 e x .

50