Фарковка

à) x 3 2

y 3 2

4;

à) x 1 2

y 4 2

25;

á)

x 2

y 2

1;

á)

x 2

y 2

1;

3

49

25

8

16

4

x

2

y

2

x

2

y

2

â)

1;

â)

1;

36

9

9

4

ã) y 2 3x.

ã) y 2 4x.

à) x 3 2

y 2 2

9;

à) x 1 2

y 1 2

16;

á)

x 2

y 2

1;

á )

x 2

y 2

1;

4

9

25

9

25

36

â)

x 2

y 2

1;

â)

x 2

y 2

1;

25

49

9

16

ã) y 2 4x.

ã)x 2 6 y.

à) x 5 2

y 3 2

4;

à) x 4 2 y 3 2

25;

á)

x 2

y 2

1;

á )

x 2

y 2

1;

5

4

49

10

16

25

â)

x 2

y 2

1;

â)

x 2

y 2

1;

16

25

25

64

ã) y 2 2x.

ã) y 2 x.

Задание 2.3. Написать канонические уравнения прямой.

Вариант			Вариант
1	2x y z 2 0		6	3x y z 6 0
		0
	2x y 3z 6			3x y 2z 0
2	x 3y 2z 0		7	x 5y 2z 11 0
		0
	x 3y z 14			x y z 1 0
3	x 2 y z 4 0		8	3x 4 y 2z 1 0
		0
	2x 2 y z 8			2x 4 y 3z 4 0
4	x y z 2 0		9	5x y 3z 4 0
	x y 2z 2 0			x y 2z 2 0
5	2x 3y z 6 0		10	x y z 2 0
	x 3y 2z 3 0			x 2 y z 4 0

Задание 2.4. Найти угол между плоскостью α и прямой, проходящей через начало координат и точку М. Вычислить расстояние от точки М до плоскости

α.

Вариант	М	α	Вариант	М	α
1	(-1;3;2)	x 2y 3z 4 0	6	(-2;4;-3)	x 5y 7z 2 0

21

2	(2;1;-3)	x y 2z 5 0	7	(5;-3;2)	x 3y 2z 14 0
3	(-2;4;2)	3x 5y z 10 0	8	(-3;-2;4)	x 5y 3z 1 0
4	(5;-1;-4)	x 2y 4z 5 0	9	(1;3;4)	2x 3y z 6 0
5	(3;1;2)	2x y 5z 3 0	10	(3;2;-1)	2x 3y z 4 0

Пример выполнения заданий по теме 2

Задание 2.1. Найти длину высоты AD в треугольнике с вершинами А (2; 1), В (-1; -1), С (3; 4) и написать уравнение перпендикуляра, опущенного из точки С на прямую АВ.

Решение.

1. Найдем длину высоты AD в треугольнике, как расстояние от точки A до прямой BC. Для нахождения уравнения прямой ВС воспользуемся

y y1

x x1

уравнением прямой

проходящей через две точки:

. Так как

y

y

x

x

2

1

2

1

x1 = – 1, y1 = – 1,

x 2

= 3, y 2 = 4, то получим

y 1

x 1

, которое равносильно

4 1

3 1

уравнению 4y + 4 = 5x + 5, из которого получаем общее уравнение прямой:

5x – 4y + 1 = 0.

Так как расстояние от точки M (x 0 , y 0 ) до прямой, заданной

общим уравнением

Ax + By + C = 0 находится по формуле d

Ax0 By0 C

,

A2 B2

то AD = d

5 2

4 1 1

=

7

.

52

( 4)2

41

2. Для нахождения уравнения перпендикуляра, опущенного из точки C на прямую AB, воспользуемся условием перпендикулярности прямых на

плоскости: l1 l 2	k 2	= –	1	. Для нахождения составим уравнение прямой
			k1

как прямой, проходящей через две точки и преобразуем полученное уравнение к уравнению с угловым коэффициентом.

Так как уравнение

прямой,

проходящей

через

две точки имеет вид:

y y1

x x1

, а А (2; 1), В (-1; -1), то имеем: x1 = 2,

y1 = 1, x 2 = –1, y 2 = –1.

y2 y1

x2 x1

y 1

x 2

Тогда уравнение прямой AB будет:

. Данное уравнение равно-

1 1

1 2

сильно уравнению:

– 3(y – 1) = –2 (x – 2), которое преобразуем к виду

y =

2

x

1

. Найдем из данного уравнения k1

=

2

. Тогда угловой коэффициент

3

3

3

прямой CK, перпендикулярной прямой AB будет равен k 2 = – 32 .

Для составления уравнения прямой CK воспользуемся уравнением прямой, проходящей через данную точку C (x 0 , y 0 ) в данном направлении:

22

	y – y 0 = k(x – x 0 ). Тогда уравнение прямой CK будет y – 4 = –					3	(x – 3),	которое
						2
	будет равносильно уравнению 3x + 2y – 17 = 0.
	Ответ: Длина высоты AD равна	7			, уравнение перпендикуляра,			опущен-
			41

ного из точки С на прямую АВ - прямой CK будет иметь вид 3x + 2y – 17 = 0.

Задание 2.2. Определить тип кривых и построить их. Для эллипса, гиперболы найти полуоси, эксцентриситет, координаты фокусов; для параболы – параметр р и координаты фокуса, для окружности – координаты центра окружности и радиус окружности.

Решение.

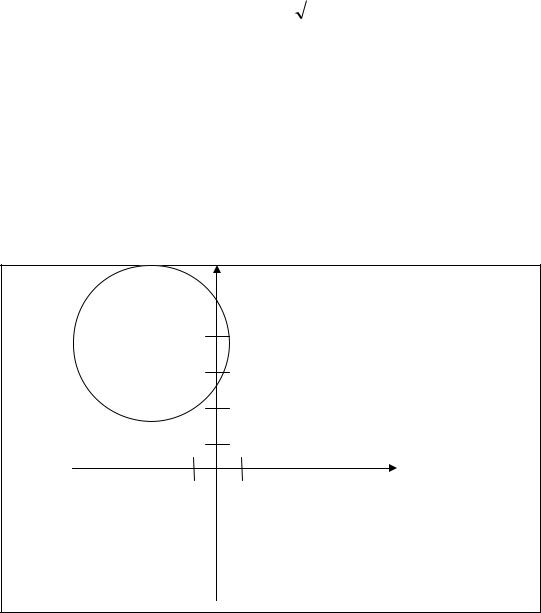
1. (x + 2) 2 + (y – 4) 2 = 9. Так как каноническое уравнение окружности имеет вид: (x - x 0 ) 2 + (y – y 0 ) 2 = R 2 , то уравнение (x + 2) 2 + (y – 4) 2 = 9, которое сводится к уравнению (x – (–2)) 2 + (y – 4) 2 = 3 2 , определяет окружность с центром в точке O'(–2; 4) и R = 3. Изобразим ее.

y

4

-2		0						x

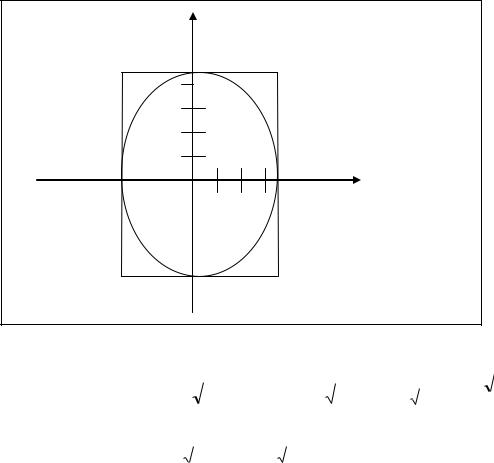
2.

x2

y 2

1.

Так как каноническое уравнение

эллипса

имеет

вид:

9

16

x2

y 2

1, то

преобразовав исходное уравнение к

виду:

x2

y2

1

,

мы

a2

b2

32

42

получим уравнение эллипса с полуосями: a = 3, b = 4. Так как b > a

, то

фокусы данного эллипса находятся на оси OY. Изобразим данный эллипс.

23

y

x

Так как эксцентриситет эллипса с фокусами на оси ординат находится по

формуле

c

и

7

0,66 .

, где c =

b2 a2 , то c =

42 32 =

7

b

4

Координаты фокусов эллипса для случая b > a имеют вид F1 (0; – c), F 2 (0; c),

	поэтому будут: F1 (0; –																	7 ), F 2 (0;			7 ).
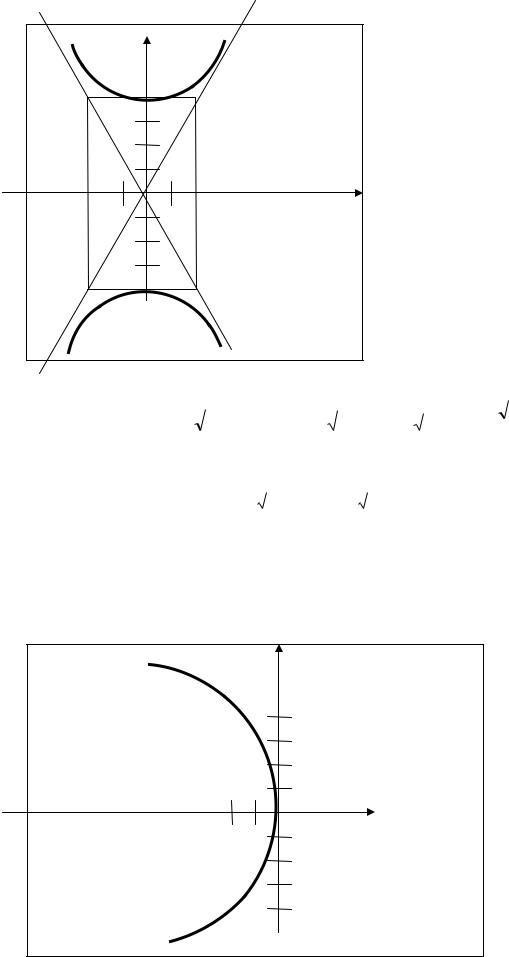
	3.			x2				y 2		1 . Так							как			каноническое уравнение гиперболы					имеет		вид:
			4					16
	2		2
		x			y			1			(		для			случая,				когда	фокусы гиперболы расположены на						оси
		2			2
		a			b
											2		2
	абсцисс) и									x				y		1 (для случая, когда фокусы гиперболы расположены на
										a	2			2
														b
																					2				2
	оси ординат),												то преобразовав исходное уравнение к виду:										x		y	1	, мы
																							2		2
																					2				4

получим уравнение гиперболы с полуосями: a = 2, b = 4 и фокусами, расположенными на оси ординат. Изобразим данную гиперболу.

24

y

x

Так как эксцентриситет гиперболы с фокусами на оси ординат находится по

формуле

c

20

1,12 .

a2 b2

, то c = 22 42

, где c =

=

20

и

4

b

Координаты фокусов гиперболы для случая

x2

y2

1 имеют вид F

(0; – c),

2

1

a

b

2

F 2 (0; c), поэтому будут: F1 (0; –

20 ), F 2 (0;

20 ).

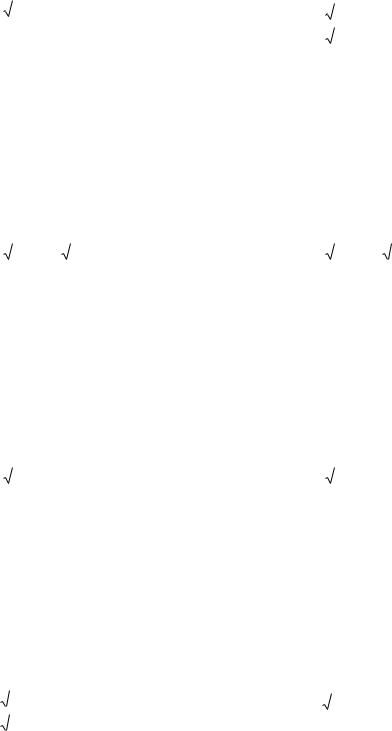
4. y 2 = - 8x. Это уравнение параболы, каноническое уравнение которой имеет вид y 2 = - 2px. Парабола имеет вершину в точке О (0; 0) и располагаться во второй и третьей четверти. Параметр параболы p = 4. Для построения параболы найдем координаты хотя бы одной точки. Если x = - 2, то y = 4.

Тогда график параболы будет следующий:

y

1

-1

x

25

Так как координаты фокуса для параболы, заданной уравнением y 2 = - 2px, имеют вид F ( 2p ; 0), то для данной параболы координаты фокуса будут

F (-2; 0).

2x y 3z 1 0,

Задание 2.3. Написать канонические уравнения прямой 5x 4 y z 7 0.

Решение.

Для нахождения канонического уравнения прямой, найдем координаты любых двух точек этой прямой.

1. Примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений, тогда получим:

y 3z 1,			y 3z 1,				y 3z 1,		y 2,
	0			z 7	0					, т.е. А(0, 2, 1).
4 y z 7			12z 4				z 1		z 1

2. Примем ее координату z = 0, а затем подставим это значение в заданную систему уравнений, тогда получим:

																																														9
y 2x 1,																					y 2x 1,																y 2x 1,							y					,
																																														1113
5x 4 y 7 0																					5x 8x 4 7 0																13x 11												,			т.е.
																																												x
																																														13
B(				11	,	9		,0 ). Воспользуемся уравнением прямой, проходящей через две точки:
			13 13
	x x1									y y1									z z1
																											.	Подставим								координаты					точек				A				и	B		в данное
	x			x						y		y							z				z
		2	1								2				1					2	1
													x 0										y 2							z 1				x			y 2		z 1			x			y 2					z 1
уравнение:																																																			.
												11			0						9				2					0 1			11				17		1			11			17					13
												13											13									13					13
										x 0							y 2										z 1
Ответ:																														.
								11									17										13
Задание 2.4.															Найти угол между плоскостью																								α: x + 2y – z + 1 = 0													и прямой,

проходящей через начало координат и точку М (2; 1; -2). Вычислить расстояние от точки М до плоскости α.

Решение.

1. Воспользуемся формулой для вычисления угла между прямой и плоскостью:

sin =		Am Bn Cp				, где	n ( A; B;C) – нормальный вектор
		A2 B2 C 2 m2 n2 p 2
плоскости	α, a (m; n; p) - направляющий						вектор прямой. Для нахождения

уравнения прямой воспользуемся уравнением прямой, проходящей через две

точки:

x x1

y y1

z z1

. Так как М (2; 1; -2), O (0; 0; 0), то уравнение

x

x

y

y

z

z

2

1

2

1

2

1

26

прямой	MO будет							иметь вид:									x		y						z		.				Тогда a (2;1; 2) , n (1;2; 1) ,
																	2
																		1					2
поэтому
											1 2 2 1 ( 1) ( 2)
sin = =																																	6						2							2 6					6
																																														6					3
			12				22 ( 1)2 22 12 ( 2)2																										3 6		6
Значит,	= arcsin		6				.
			3
2. Расстояние от точки M (x 0 ; y 0 ; z 0 )																		до плоскости α,																			заданной													уравнением x
+ 2y – z + 1 = 0 находится по формуле d =																							Ax0							By0 Cz0 D																	. Тогда
																														A2 B2 C 2
											1 2 2 1 ( 1) ( 2) 1
			d =																											7				7			6			2,86 .
													12 22 ( 1)2																	6					6
Ответ: = arcsin											6		, d 2,86.
							3

27

lim f (x) A.

x

4. Тема 3. Введение в математический анализ

Краткие теоретические сведения

Число А называется пределом функции f(x) при х , если для любого числа

> 0 существует такое число					М > 0, что для всех х, х >M выполняется
неравенство		f (x) A		.

При этом предполагается, что функция f(x) определена в промежутке (-∞;+∞). Записывают:

Число А называется пределом функции f(x) в точке a					(при х а), если для
любого > 0 существует такое		число δ > 0, что для			всех х таких, что
0 < x - a < δ верно неравенство		f (x) A		.

Первый замечательный предел математического анализа:

Второй замечательный предел математического анализа:

Основные эквивалентности при х 0:

sin x ~ x, 1 – cos x ~	x2
	2 , arcsin x ~ x, tg x ~ x, arctg x ~ x,

lim	sin x				1 .
x 0		x
			1		x	e .
lim 1
x			x

ln(1 + x) ~ x.

Задания к расчетно-графической работе

Задание 3.1. Найти пределы функций, не пользуясь правилами Лопиталя.

Вариант

Задание

Вариант

Задание

1

а)

lim

x3 1

;

6

а) lim

2x3 x2 4

;

2x3

x x3 5

x

3x2 3

x

б) lim

x2 1

;

б) lim

x2 4

;

2x2 x

x2 x

x 1

1

x 2

6

в) lim

x

;

в) lim

sin 4x

;

x 0

1 2x

1

x 0

x 1

1

г)

lim

5x

;

г) lim

arcsin 3x

;

x 0

arctg x

x 0

tg 4x

x 3

x

2x 1 x

д) lim

.

д) lim

.

x x 2

x

2x 1

28

2

а)

lim

5x

4 x3 1

;

7

а)

lim

7x2 3x 1

;

2x4 x2 3

2 14x2 x

x

x

б) lim

x 2

;

б) lim

x2 16

;

x

2

3x

2

x2 3x

4

x 2

x 4

2x x

в) lim

;

в) lim

x 1

2

;

x 2

x 2

x 3

x 2 1

sin 2x

г)

lim

;

г)

arctg 2x

;

lim

x 0 arcsin 5x

x

x 0

x

4x 1

2x

2 x

4

д)

lim

.

x

4x

д)

lim

.

x 2x 3

3

а)

lim

2x

2 6x 3

;

8

а)

lim

3 x 5x

3

;

5x2 2x 1

x

x x3 2x

1

б) lim

x2 6x 8

;

б)

lim

x2 5x 6

;

x2 8x

12

x2 9

x 2

x 3

в) lim

6 x

6 x

;

в) lim

3 x

3 x

;

x

x

x 0

x 0

г)

lim

tg 2x

;

г) lim

cos 5x cos 3x

;

x 0

sin 5x

x 0

x2

x 2

5 x

8x 8

3x

д)

lim

.

д)

lim

.

x x

3

x

8x 1

4

а)

lim

x 2x2 5x4

;

9

а)

lim

5x2 2x 2

;

2 x2 x4

6x2

2x 3

x

x

б) lim

x3 6x

2 x 6

;

б)

lim

2x3 2x2 x 1

;

x2 3x 2

x3 x2 3x 3

x 1

x 1

в) lim

x 8 3

;

в) lim

x 25 5

;

x 1

x 1

x 0

x2 2x

sin

2

3x

г) lim

cos 6x cos 2x

;

г)

lim

;

x

2

2

x 0 sin

2x

x 0

5x 7 3x

4x 4

5 x

д)

lim

.

д)

lim

.

4x

x 5x 5

x

4

5

7x

3

3x

2

2x

10

8x

2

3x 4

а) lim

;

а)

lim

;

2 x3

x 4x2 5

x

x

б)

lim

x 1

;

б)

lim

x 2 4

;

x 2 1

x 1

x 2

x 2

x

1

в)

lim

;

в)

lim

3

8 x 2

;

3

x 1

x

1

x 0

x

г) lim

1 cos x

;

г)

lim

3x

;

x 0

x2

x 0

arcsin 7x

9x 2 2 x

x 2 5

x2

д)

lim

.

д)

lim

.

5

x

9x 16

x x

2

29

Пример выполнения заданий по теме 3

Задание 3.1. Найти пределы функций, не пользуясь правилами Лопиталя.

а)

lim

3 2x 4x2

;

3x2 12

x

б) lim

2x2 5x 3

;

x2 9

x 3

lim

1 x x2 1 x x2

в)

x2 x

;

x 0

г)

lim

arcsin x tg 2x

;

x 0

1 cos x

3x 2 2 x

д) lim

.

x

3x 5

Решение.

а). Разделим числитель и знаменатель дроби на наибольшую степень: x 2 . Тогда

																					3				2			4
					lim	3 2x 4x2									= limx						x2					x
получим:											=														12					.	Так		как			при x
							3x		2	12
					x
																					3
																										x2
														3			2		4
3				2		12							x2														0 0 4					4		1
			0,		0,			0 , то			lim							x						=									1		.
	x	2		x		x	2										12											3 0				3
											x																							3
														3
																		x2

б) Разложим числитель и знаменатель дроби на множители.

Найдем корни многочлена 2x 2 - 5x – 3. Так как D = (–5) 2 – 4·2·(–3) = 49,

	x1	5 7	3 ,	x 2	=	5 7		1	. Тогда применив формулу:
		2 2				2 2		2

ax 2 + bx + c = a(x - x1 )·(x - x 2 ), получим 2x 2 - 5x – 3 = 2(x - 3)·(x - 12 ).

то

Так как x 2 - 9 = (x – 3)(x + 3),

			2x2 5x 3			2(x 3)(x	1	)
										2x 1			2 3 1			7		1
	то	lim			= lim		2		lim								1		.
			x2 9
						(x 3)(x 3)				x 3			3 3			6		6
		x 3			x 3				x 3

в) Домножим числитель и знаменатель дроби на сопряженное выражение:

lim

1 x x2

1 x x2

=

x2

x

x 0

= lim

1 x x2 1 x x2

lim

2x

=

x(x 1)(

1 x x2

1 x x2 )

1 x x2

x 0

x 0 x(x 1)(

1 x x2 )

30