Фарковка

=

2

2

1 .

(x 1)( 1 x x2

1 x x2 )

1 (1 1)

2

x

x

2

при х 0, то

г) Так как 1 – cosx =

2sin

~ 2

, arcsin x ~ x, tg2x ~

2x

2

2

lim

arcsin x tg 2x

lim

x 2x

4.

x 0

1 cos x

x 0

x2

2

д) Преобразуем

выражение

под

знаком

предела

таким

образом, чтобы

1 x

применить формулу второго замечательного предела:

lim 1

e .

x

x

3x 2 2 x

2 x

3x 5

7

7

7

( 2 x)

7

3x 5

lim

= lim 1

= lim 1

=

x 3x

5

x

3x 5

x

3x

5

14x

3x 5

3x 5

lim 14x

7

7

14

1

= lim

1

= e x 3x 5

= e 3 =

.

3x

5

x

e4 3 e2

Ответ:

а) lim

3 2x 4x2

= –1

1

;

3x2 12

x

3

б)

в)

г)

д)

lim

2x2 5x 3

1

x2 9

= 1 6 ;

x 3

lim

1 x x2

1 x x2

= –1;

x2

x

x 0

lim

arcsin x tg 2x

= 4;

x 0

1 cos x

3x 2 2 x

1

lim

=

.

x

3x 5

e4 3 e2

31

x x0

5. Тема 4. Дифференциальное исчисление функции одной переменной

Краткие теоретические сведения

Производной функции f(x) в точке х0 называется предел отношения приращения функции в этой точке к приращению аргумента, когда приращение

			f (x x) f (x)
	аргумента стремится к нулю:	f (x) lim		.
			x
		x 0

Теорема о производной сложной функции. Если функция u = φ(x) имеет производную в точке x, а функция y = f(u) имеет производную yu/ в соответствующей точке u = φ(x), то сложная функция y = f(φ(x)) имеет

производную yx/	в точке x , которая находится по формуле:		yx/ yu/ ux/ .
Теорема (правила Лопиталя). Если функции f(x) и g(x)			дифференцируемы
вблизи точки а,	непрерывны в точке а, g (x) отлична от		нуля	вблизи	а и
f(a) = g(a) = 0 (или lim f (x) lim g(x) ), то предел отношения				функций	при
	x a	x a

х а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует:

lim	f (x)	lim	f (x)	.
x a	g(x)	x a	g (x)

Теорема (достаточные условия возрастания и убывания функции).

1.Если функция f(x) дифференцируема на интервале (a, b) и f (x) > 0 для любого x (a, b), то функция возрастает на интервале (a, b).

2.Если функция f(x) дифференцируема на интервале (a, b) и f (x) < 0 для любого x (a, b), то функция убывает на интервале (a, b).

Точка x0 называется точкой такая δ - окрестность точки x0 выполняется неравенство f(x) < f(

максимума функции y = f(x), если существует , что для всех из этой окрестности x0 ).

Точка x0 называется точкой минимума функции y = f(x), если существует

такая δ - окрестность точки	x0 , что для всех x x0 из этой окрестности
выполняется неравенство f(x)	> f( x0 ).

Точки максимума и минимума функции называются точками экстремума функции.

Значение функции в точке максимума называется максимумом функции. Значение функции в точке минимума называется минимумом функции. Максимумы и минимумы функции называются экстремумами функции.

32

Теорема (необходимое условие существования экстремума).

Если функция f(x) дифференцируема в точке x0 и точка x0 является точкой экстремума, то производная функции обращается в нуль в этой точке.

Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.

Теорема (достаточные условия существования экстремума) .

1. Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку x0 , и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки x0 ). Если при переходе через точку x0 слева направо производная функции f (x) меняет знак с плюса на минус, то в точке x0 функция f(x) имеет максимум, а если производная меняет знак с минуса на плюс, то в точке x0 функция f(x) имеет минимум.

2. Пусть в точке x0 f ( x0 ) = 0 и

f ( x0 ) существует и непрерывна в

некоторой окрестности точки x0 . Тогда, если f ( x0 ) < 0, то функция имеет в точке x0 максимум, а если f ( x0 ) > 0, то функция имеет в точке x0 минимум.

График дифференцируемой функции y = f(x) называется выпуклым на интервале (a, b) , если он расположен ниже любой ее касательной на этом интервале.

График дифференцируемой функции y = f(x) называется вогнутым на интервале (a, b) , если он расположен выше любой ее касательной на этом интервале.

Теорема (достаточные условия выпуклости (вогнутости) графика функции). Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то график функции y = f(x) выпукл. Если во всех точках интервала (a, b) вторая производная функции f(x) положительна, то график функции y = f(x) вогнут.

Точка, отделяющая выпуклую часть графика функции от вогнутой,

называется точкой перегиба.

Теорема (достаточное условие существования точек перегиба). Если вторая производная f (x) при переходе через точку x0 , в которой она равна нулю или не существует, меняет знак, то точка графика функции с абсциссой x0 является точкой перегиба.

Асимптотой кривой называется прямая, к которой сколь угодно близко

приближается график функции.
Прямая x = a		называется вертикальной		асимптотой графика функции
y = f(x), если	lim	f (x) или	lim f (x)	или lim f (x) .
	x a 0		x a 0	x a

33

Прямая	y = b	называется		горизонтальной асимптотой					графика функции
y = f(x), если lim		f (x) b или		lim f (x) b .
	x			x
Прямая	y = kx + b называется наклонной						асимптотой		графика функции
y=f(x), если:
			k lim		f (x)	( k lim	f (x)	) и
			x		x	x	x
		b =	lim ( f (x) kx) (b = lim ( f (x) kx) .
			x			x

Задания к расчетно-графической работе

Задание 4.1. Найти производные y данных функций.

Вариант

Задание

Вариант

Задание

1

a) y

ln x

x

6

а) y

cos x

;

;

tgx

cos x

1 2sin x

б) y = sin 4

x

б) y = cos

3 4x

3

4

2

а) y

2sin x

;

7

а)

y

1 e x

;

1 cos x

1 e x

б) y = cos ln(1 - x 2 )

б) y = ln 5

x

5

3

а) y

xarctgx

;

8

а)

y

x

arctgx ;

1 x2

1 x2

б) y = e

arcsin(2 x 4)

б) y = ln (x – cos 3x)

4

x

1

x

9

ln x

x

а) y 3x arctg

arctg

;

а)

y

3

3

3

ctgx

sin x

б) y =ln (2 - cos 2 x)

б)

y

x arcsin x

1 x ;

5

а) y

3cos x

10

а)

y

1 e x

1 cos x

1 e x

б) y ln

1 x2

б)

y ln tg

2x 1

;

1 x2 .

4

Задание 4.2. Исследовать функцию						y f x		и построить ее график.
Вариант		Задание				Вариант				Задание
1	y	4x	2 .			6		y x 1 .
								2
		4 x
									x 2	1

34

2

y

x 2

1

.

7

y

x 2

.

x 2

1

x

1

3

y

x

3

.

8

y

4x3

5

.

x 2

1

x

4

y

x2

5

.

9

y

x

4

.

3

x3

x

1

5

y

4x3

.

10

y

2 4x2

.

x3

1

1

4x2

Пример выполнения заданий по теме 4

Задание 4.1. Найти производные

y

данных функций.

а)

y

x 2 e x2

;

б) y ln tg

x

x

x 2

1

sin x

2

Решение.

а)

Для

нахождения

производной

воспользуемся правилом

нахождения

u '

u ' v u v'

производной частного

и производной сложной функции:

v2

v

x 2 e x2

/

x2

e x2 ' (x2 1) (x2 e x2 ) (x2 1)'

y' = x 2 1 =

(x2 1)2

=

=

(2x e x2

x2

e x2 2x) (x2 1) x2 e x2 2x

=

(x2 1)2

2x3e x2

2x5e x2

2xe x2

2x3e x2

2x3e x2

2xe x2

(x4 1 x2 )

.

(x2 1)2

(x2 1)2

б) Для нахождения производной функции применим правила нахождения производной разности и производной частного, а также дважды применим правило нахождения производной сложной функции:

'

x

x

'

x

'

x

'

1

x

'

x'

sin x x(sin x)'

y

(ln tg

)

(ln tg

)

=

tg

x

sin 2 x

2

sin x

2

sin x

tg

2

2

cos

x

1

1

1

sin x x cos x

sin x x cos x

2

=

=

tg

x

cos

2 x

2

sin 2 x

sin

x

cos

2 x

2

sin 2 x

2

2

2

2

=

1

sin x x cos x

1

sin x x cos x

sin x sin x x cos x

x cos x

x

x

sin 2 x

sin x

sin 2 x

sin 2 x

sin 2 x

2sin

cos

2

2

35

	Задание 4.2. Исследовать функцию	y	x3			и построить ее график.
			x 2	1

Решение.

При исследовании функции будем придерживаться следующей схемы:

1.Найдем область определения функции.

2.Найдем точки пересечения графика функции с осями координат.

3.Исследуем функцию на четность и нечетность.

4.Найдем асимптоты графика функции.

5.Найдем y' и с помощью ее определим промежутки возрастания и убывания функции, экстремумы функции.

6.Найдем y'' и с помощью ее определим промежутки выпуклости и вогнутости графика функции и точки перегиба.

7.Используя пункты 1 – 6 данной схемы строим график функции, в случае затруднения берем несколько дополнительных точек.

	1. Так как дробь	x3			определена при всех значениях x 1, то областью
		x2	1

определения функции будет D(f) = (- ; -1) (-1; 1) (1; + ).

x3

2. а) Найдем точки пересечения с осью абсцисс: y = 0, поэтому x2 1 = 0,

откуда x = 0. Таким образом, получаем точку пересечения с осью OX: точку O

(0; 0).

б) Найдем точки пересечения с осью ординат: x = 0,

тогда y =

03

0 . В

0

2

1

итоге получаем ту же точку O (0; 0).

3. Найдем y (-x) =

( x)3

=

x3

= – y(x), то есть функция

y

x3

является

( x)2 1

x2 1

x 2

1

нечетной.

4. а) Найдем вертикальные асимптоты графика функции. Найдем

lim

x3

=

1

,

lim

x3

=

1

. Значит, прямая x = 1 является

x2

1

x2 1

0

x 1 0

x 1 0

0

вертикальной асимптотой графика функции

y

x3

.

x 2 1

Найдем

lim

x3

=

1

,

lim

x3

=

1

. Значит, прямая x = - 1

2 1

x2 1

x 1 0 x

0

x 1 0

0

является вертикальной асимптотой графика функции

y

x3

.

x 2 1

36

б) Найдем горизонтальные асимптоты графика функции. Для этого найдем

lim

x3

lim

3x2

lim

3

x = +

. (При вычислении предела

2

1

=

=

=

x x

x

2x

x

2

применили правило Лопиталя).

Аналогично,

lim

x3

= -

. Поэтому горизонтальных асимптот график

x x2 1

функции не имеет.

в) Найдем

наклонные

асимптоты

графика

функции. Так

как

наклонная

x3

асимптота имеет вид

y = kx + b, то найдем k

и b. k =

lim

y

=

lim

x2 1

=

x

x

x

x

lim

x3

lim

x2

= lim

2x

=

1.

Аналогично,

lim

y

=

1.

Таким

1

x

x x(x2 1)

x x2

x 2x

x

x3

x3

x (x2 1)

образом,

k = 1.

b =

lim (y – kx)

=

lim

1 x =

lim

=

2

1

x

2

1

x

x

x

x

x3

x3

x

x

x /

1

= lim

= lim

=

= lim

= lim

= 0.

x

2

1

x x

2

1

(x

2

1)

/

x 2x

x

x

Значит, график функции имеет наклонную асимптоту y = x.

5. Найдем производную функции y

x3

:

x 2 1

3x2 (x2 1) 2x x3

3x4 3x2 2x4

x4 3x2

x 2 (x2 3)

y

(x2

1)2

(x2 1)2

(x2 1)2

= (x2 1)2 .

x 2

(x2

3)

Решая уравнение

= 0, находим критические точки: x = 0; x = - 3 ; x =

(x2

1)2

3 ; x = -1; x = 1.

Найдем промежутки возрастания и убывания функции.

Для этого определяем знаки производной функции на промежутках.

									y > 0, функция возрастает
x < - 3 ,
									y < 0,
-		3 < x < -1,								функция убывает
-1 < x < 0,									y < 0,	функция убывает
0		< x < 1,							y < 0,	функция убывает
									y < 0, функция убывает
1		< x < 3 ,
									y > 0, функция возрастает
	3 < x ,

Так как при переходе через точку х = - 3 знак производной функции меняется с «плюса» на «минус», то точка х = - 3 является точкой максимума. А так как

37

	при переходе через точку х =			3	знак производной функции											меняется с
	«минуса» на «плюс», то точка х =					3 является точкой минимума. Значения
	функции в этих точках равны: y		= y(-						) = -	3 3			-2,6, y		= y(		) =	3 3			-
		max						3						min		3
					2											2
	2,6.

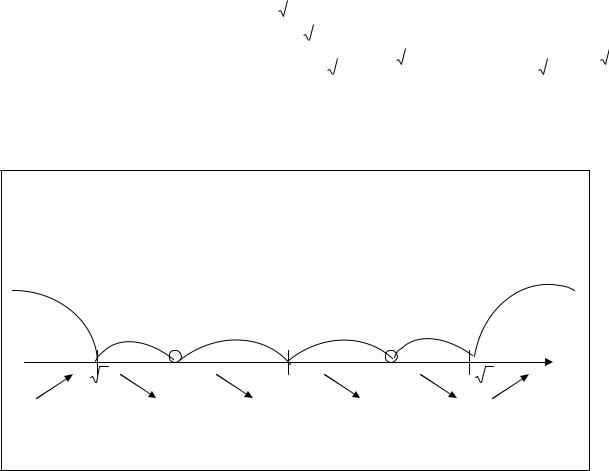
Данные проведенного исследования можно кратко изобразить на следующей схеме:

		max				min
y '	+	-	-		-	-	+
y		- 3	-1	0	1	3	x

6. Найдем вторую производную функции

y

(4x3 6x)(x2 1)2

(x4 3x2 )4x(x2 1)

(x

2 1)4

(4x3

6x)(x4

2x2 1) (x4 3x2 )(4x3

4x)

(x2

1)

4

4x7

8x5 4x3 6x5 12x3

6x 4x7 4x5 12x5 12x3

(x2

1)

4

2x5 4x3 6x

2x(x4

2x2 3)

2x(x2 3)(x2

1)

2x(x2

3)

.

(x2

1)4

(x2 1)4

(x2 1)4

(x

2

1)3

Определим выпуклость и вогнутость графика функции на промежутках:

x < -1,	y < 0,	кривая выпуклая
-1 < x < 0,	y > 0,	кривая вогнутая
0 < x < 1,	y < 0,	кривая выпуклая
1< x ,	y > 0, кривая вогнутая

Таким образом, точка O (0; 0) – точка перегиба графика функции. Данные проведенного исследования можно изобразить схематически:

38

			перегиб
y "	-	+	-	+
y		-1	0	1	x
7.	Используя данные проведенного исследования, построим				график функции.
Для уточнения найдем несколько точек графика функции:

x	0,5	2	3
y	-0,2	2,7	3,4

		4
		3
		2
		1
- 2	- 1	1	2
		- 1
		- 2
		- 3
		- 4

39

6. Тема 5. Интегральное исчисление функции одной переменной

Краткие теоретические сведения
Функция F(x) называется первообразной функцией	функции f(x) на
промежутке X, если для любого x из данного промежутка	X верно равенство:
F (x) = f(x).

Неопределенным интегралом от функции f(x) называется множество всех первообразных функций F(x) + C для функции f(x).

Записывают: f (x)dx F(x) C .

Основные свойства неопределенного интеграла:

1.f (x)dx f (x);

2.d f (x)dx f (x)dx;

3.dF(x) F(x) C;

4.( f (x) g(x))dx f (x)dx g(x)dx ;

5.k f (x)dx k f (x)dx , где k R, k 0.

Метод интегрирования подстановкой (заменой переменной):

f (x)dx f ( (t)) (t)dt .

Метод интегрирования по частям: udv uv vdu ;

n

Если существует конечный предел интегральной суммы Sn f (ci ) xi при

i 1

n ,	не зависящей ни от способа разбиения отрезка [a, b]на части, ни от
выбора	точек ci , то этот предел называется определенным интегралом от

функции y = f(x) на отрезке [a, b].

b		n
Обозначается: f (x)dx.	= lim f (ci ) xi , а – нижний предел, b – верхний
a	n	i 1

предел интегрирования, х – переменная интегрирования, [a, b] – отрезок интегрирования.

Основные свойства определенного интеграла:

b c b

1) Для любых a, b, c верно ( f (x)dx f (x)dx f (x)dx ;

a a c

40