∞

sin n

25 ∞

(

1)n

X

−

−

nX

−

91)

,

92)

−

,

n=1

√n + (

1)n

1

=1

√n + (

1)n sin n

93)

∞

sin n

,

94)

∞

(−1)n

.

nX

X

−

=1 n ln n + 5 sin n

n=1

√n ln n + ( 1)n

1.3.2. Найти α, при которых следующие ряды а) сходятся абсолютно; б) сходятся условно :

1)

∞

(−1)n−1

,

2)

∞

(−1)n−1

arcsin

1

,

X

nX

nα

√n

n=1

=1 nα + 1 ·

3)

∞

(−1)n

,

4)

∞ ln(1 +

(−1)n−1

),

X

nα + 1/n

nX

nα

n=1

=1

5)

∞

(−1)n

,

6)

∞

(−1)n−1

,

X

nX

−

1)n)α

−

n=1 (2n + (

=1 (√n + ( 1)n)α

7)

∞

cos n

, α > 0,

8)

∞

sin 2n

ln2 n.

X

nX

nα

nα

n=1

=1

2 Функциональные последовательности и ряды

Материал данной темы можно изучить, например, по учебникам [1], стр. 540-592, или [2], стр. 419-450.

2.1Поточечная и равномерная сходимость функциональной последовательности

Пусть дана последовательность функций {fn(x)}, где fn : X R1 → R1, n N. Точка x0 называется точкой сходимости этой последовательности, если x0 X и числовая последовательность {fn(x0)} сходится.

Совокупность всех точек сходимости функциональной последовательности {fn(x)} называется множеством сходимости (областью сходимо-

26	( X)	является областью сходи-
сти) этой последовательности. Если X1

мости последовательности {fn(x)}, то говорят, что функциональная последовательность поточечно сходится на множестве X1, при этом функцию

f : x X1	7−→nlim fn(x) называют предельной функцией данной после-
	→∞	X
довательности и пишут f(x) = nlim→∞ fn(x) на X1		или fn(x) −→ f(x) при
n → ∞.		X

В терминах ”ε − N” поточечная сходимость fn(x) −→ f(x) означает,

что по любому ε > 0 и для каждой точки x X1 найдётся номер N = N(ε, x) такой, что для n > N выполняется неравенство |fn(x) − f(x)| < ε,

т.е. f(x) − ε < fn(x) < f(x) + ε.

Пример 2.1. Найти область сходимости последовательности {fn(x)}, если fn(x) = xn, x [0; +∞).

B Так как

nlim x	n	=		0,	если x [0; 1),	.
				1,	если x = 1,
−→∞				∞,	если x > 1

то последовательность поточечно сходится на множестве [0; 1] и её предельной функцией является

f(x) =		0,	если x [0; 1), . .
		1,	если x = 1

Определение 1. Пусть последовательность {fn(x)} поточечно сходится на множестве X к функции f(x) и B X. Последовательность {fn(x)} называется равномерно сходящейся на множестве B, если для любого ε > 0 можно указать такой номер N = N(ε), что выполняется неравенство |fn(x) − f(x)| < ε для всех n > N и всех x B. При этом пишут

B

fn(x) f(x).

Обратите внимание, в случае поточечной сходимости последовательности {fn(x)} к функции f(x) на B, номер N, соответствующий числу ε > 0, зависит не только от ε, но и от точки x, а в определении 1 не

27

(рис.1)

B

зависит от x. Если fn(x) −→ f(x), но не удовлетворяет определению 1, то говорят, что последовательность сходится к f(x) неравномерно на множестве B. Если же последовательность сходится неравномерно на B или расходится хотя бы в одной точке этого множества, то говорят, что последовательность не является равномерно сходящейся на множестве B.

B

Геометрически факт fn(x) f(x) означает, что для любой ε− полосы, окружающей на множестве B график функции f, найдётся такой номер N = N(ε), что для любого n > N графики функций fn(x) расположены в этой ε− полосе (рис.1).

Проиллюстрируем определение равномерной сходимости на примере.

Пример 2.2. Исследовать на равномерную сходимость последовательность fn(x) = xn

a)на [0; q], q (0; 1);

b)на [0; 1).

B Ранее было показано, что f(x) = nlim→∞ fn(x) = 0, x [0; 1).

[0;q]

а) Докажем, используя определение, что fn(x) 0 Зафиксируем произвольное ε (0; q) и найдём номер N такой, что |xn − 0| < ε для n > N и x [0; q]. Так как qn < ε n > lnln qε, то взяв N = "lnln qε# , получим нужное. Геометрически: графиком предельной функции f является отрезок оси Ox

— [0; q]. Фиксируем произвольную ε−полосу (0 < ε < 1) графика предельной функции. Так как fn(x) = xn ≥ 0 при x [0; q], то можно рассматривать

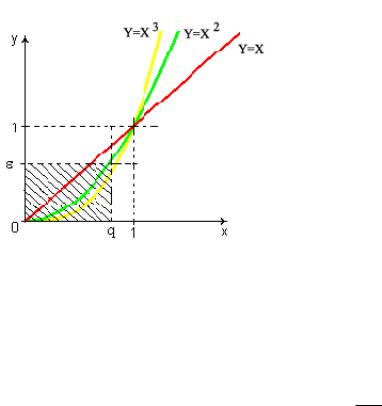
28

(рис.2)

только часть полосы, лежащую в верхней полуплоскости (ею является прямоугольник [0, q] × [0, ε)).

Графики функций fn при n > N = "lnln qε# лежат в этой ε−полосе (рис.

2)

б)Покажем, что fn(x) → 0 на [0; 1) неравномерно. Что означает этот факт?

B

fn(x) 6 f(x) ε0(> 0), xnk B (n1 < n2 < ... < nk < ...)

такие, что |fnk (xnk ) − f(xnk )| ≥ ε0(k = 1, 2, ...). В данном случае нам подхо-

1

дит, например, ε0 = 31 . Действительно, для точек xn = √n

[0; 1) имеем

3

|

fn(xn)

−

f(xn)

|

=

n1

!n

0

=

1

= ε0.

√3

−

3

Итак, последовательность fn(x) = xn поточечно, но неравномерно сходится к функции f(x) ≡ 0 на [0; 1). Это очевидно и из геометрических соображений. Именно, какую бы ε− полосу графика функции f на [0; 1) мы ни взяли (0 < ε < 1), графики функций fn(x) "выскакивают"из неё.

29 При исследовании равномерной сходимости функциональной после-

довательности рассуждения, как правило, упрощаются, если использовать критерий равномерной cходимости:

B

1. (Критерий в терминах супремумов) Пусть fn(x) → f(x) при n → ∞

и αn = sup |fn(x) − f(x)|, n N. Для того чтобы последовательность

x B

{fn(x)} равномерно сходилась к функции f(x) на множестве B, необходимо и достаточно, чтобы lim αn = 0.

2.(Критерий Коши) Для того чтобы последовательность {fn(x)} равномерно сходилась на множестве B необходимо и достаточно, чтобы

ε > 0 N = N(ε) N : n > N, p N, x B выполнялось неравенство |fn+p(x) − fn(x)| < ε.

Если условие Коши не выполняется, т.е. ε0 > 0 : N N n > Np N xe B : |fn+p(xe) − fn(xe)| ≥ ε0, то последовательность {fn(x)} не является равномерно сходящейся на множестве B.

Если, например,

ε0 > 0 : n N pn N xn B : |fn+pn(xn) − fn(xn)| ≥ ε0, (1)

то последовательность {fn(x)} не является равномерно сходящейся на B. Возвращаясь к примеру 2.1, изучим поведение последовательности

{fn(x)} : fn(x) = xn на множествах а) B = [0; 1−δ], δ (0; 1) и б) B = [0; 1),

используя приведённые критерии.

	y = x	nЕсли x [0; 1 − δ], δ (0; 1), то |fn(x) − f(x)| = xn, n N. Функция
		является возрастающей на [0; 1 −δ], поэтому sup |fn(x) −f(x)| =
	(1 − δ)n = 0, то есть αn = (1 − δ)n, n N.										x [0;1−δ],
										[0;1−δ]
		Поскольку nlim (1 − δ)		n	= 0, то fn(x)
										0.
		Если же x	→∞ , то		f	n(	x	) −	f x		lim xn = 1. Следовательно,
			[0; 1)	sup |						(	)| = x 1
											→
			x [0;1)
		[0;1)
	αn 6→0 и fn(x) 6 0.

30

Получим последний результат с помощью критерия Коши. Для любого

n N положим xn = 1 − n1 , pn = n. Тогда

!

!

! .

1

n

1

n

|fn+p(xn) − fn(xn)| = |xnn+p − xnn| = xnn|xnn − 1| = 1 −

· 1 −

1 −

n

n

− n

e

3e

Так как lim 1

1

!n =

1

, то последнее произведение больше

1

,

n > n0.

Следовательно, считая ε0 = 31e и используя критерий Коши, заключаем,

что последовательность {xn} не является равномерно сходящейся на промежутке [0; 1).

Наконец, вопрос о равномерной сходимости последовательности {fn(x)} к предельной функции иногда решается с помощью теоремы о непрерывности предельной функции равномерно сходящейся функциональной последовательности и с помощью теоремы Дини:

1. Если все члены функциональной последовательности {fn(x)} непре-

B

рывны на множестве B и fn(x) f(x), то f(x) C(B).

Следствие 1. Если все члены последовательности {fn(x)} непре-

B

рывны на B, fn(x) −→ f(x) и f(x) терпит разрыв хотя бы в одной точке множества B, то последовательность сходится на B неравномерно.

2.(Теорема Дини. ) Если fn(x) непрерывны на компакте B, n N, последовательность {fn(x)} монотонна по n в каждой точке x Bи

B

предельная функция f(x) C(B), то fn(x) f(x).

Снова возвращаясь к примеру 2.1, замечаем, что на множестве [0; 1]

[0;1]

выполняются условия приведённого следствия, поэтому fn(x) 6 f(x), а на отрезке [0; 1 − δ], δ (0; 1) выполняются условия теоремы Дини, значит

[0;1−δ]

fn(x) f(x).

2.1.1. Исследуйте на поточечную и равномерную сходимость последовательность {fn(x)} на указанном множестве:

1.

fn(x) = x

2n

,

a)

31

x [0; q], q (0; 1); b) x [0; 1];

2.

fn(x) = xn − xn−1, x [0; 1];

3.

sin nx

R.

fn(x) =

, x

n

4.

fn(x) = xn − x2n, a)x [0; 1]; b)x [0, q], q (0; 1);

5.

fn(x) =

1

, x

≥ 0;

x + n

6.

fn(x) = xn − x3n, a)x [0; q], q (0; 1); b) x [0; 1];

7.

fn(x) =

1

, a) x [0; 1],

b) [q; 1] , где q (0; 1);

x2 + nx + 1

8.

fn(x) =

nx

, x [0; 1];

1

+ n + x

9.

fn(x) =

xn

, a) x [0; q], q (0; 1), б)x [1 − ε, 1 + ε], ε (0; 1),

1

+ xn

в) x [q; +∞], q > 1;

10.

fn(x) = e−(x−n)2 ,

a) x [−q; q], q (0; +∞); б) x R;

11.

fn(x) = arctg nx,

a) x [0; 1], б) x [q; +∞), q > 0;

12.

fn(x) = n arctg nx,

x [0; a], a R+;

13.

fn(x) =

nx

,

x [q; +∞], q > 0;

1

+ n3x2

14.

fn(x) = ln(x2 + n1 ),

a) |x| > 1, б)

x (0; +∞);

15.

fn(x) =

2nx

,

a) x [0; 1] б) x (1; +∞);

1

+ n2x2

16.fn(x) = cos n1 , |x| < a, a R+;

17.fn(x) = sin nx , x R;