oin

		t2
		S = ∫v(t)dt .		[12]
		t1
Вычисление статических моментов и координат центра
		тяжести плоской кривой
Пусть	на плоскости Oxy задана система			материальных	точек
M1 (x1; y1 ) ,	M 2 (x2 ;	y2 ) , …..	M n (xn ; yn ) соответственно с массами
m1, m2 ,....mn .
Статическим		моментом Sx системы		материальных	точек

относительно оси Ox называется сумма произведений масс этих точек

на

их

ординаты

(т.

е.

на

расстояния

этих точек

от

оси Ox ):

n

Sx

= ∑mi × yi .

i=1

Аналогично определяется статический момент Sy этой системы

n

относительно оси Oy : Sy = ∑mi × xi .

i=1

Если массы распределены непрерывным образом вдоль некоторой

кривой,

то

статический

момент S (x)

однородной

кривой

AB

b

относительно

оси

Ox

равен

Sx = γ ∫ y ×

1 + ( y¢x )2 dx , где

y = f (x)

−

a

уравнение кривой AB с постоянной линейной плотностью γ

(рис. 12);

Аналогично находим Sy :

b

Sy = γ ∫ x × 1 + (x¢y )2 dy .

a

Статические моменты S (x) и Sy кривой позволяют легко установить положение её центра тяжести (центра масс).

21

Рис. 12

Центром тяжести материальной плоской кривой y = f (x) ,

x [a;b] называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу m заданной кривой, то статический момент этой точки относительно любой

координатной оси будет

равен

статическому

моменту всей

кривой

y = f (x) относительно той же оси.

Обозначим через C(xc ; yc )

центр

тяжести кривой AB .

Из определения центра тяжести следуют равенства

m × xc

= Sy и m × yc = Sx , где m = γ l .

Отсюда

xc =

Sy

,

yc =

Sx

γ l

γ l

или

b

b

∫ x ×

1 + ( y¢x )2

dx

∫ y ×

1 + ( y¢x )2

dx

x

=

a

;

y =

a

.

b

b

c

c

∫

1 + ( y¢x )2

dx

∫

1 + ( y¢x )2

dx

a

a

22

Вычисление статических моментов и координат центра

тяжести плоской фигуры

Пусть дана материальная плоская фигура (пластинка), ограниченная кривой y = f (x) > 0 и прямыми y = 0 , x = a , x = b

(рис. 13).

Рис. 13

Будем считать, что поверхностная плотность пластинки постоянна

b

(γ − const ). Тогда масса «всей пластинки m = γ ∫ f (x)dx ,

элементарные

a

статические моменты относительно осей Ox и Oy :

2

b

b

∫

∫

S

=

1

γ

y2dx ,

S

= γ

xydx

x

y

a

a

По аналогии с плоской кривой получаем, обозначив координаты

центра тяжести

плоской

фигуры

(пластинки)

через

C(xc ; yc ) , что

S

= m × x , S

= m × y . Отсюда

x =

Sy

=

Sy

и y

=

S

x

=

S

x

.

m

γ S

m

γ S

y

c

x

c

c

c

b

1

b

∫ xydx

∫ y2dx

или x

=

a

,

y

=

2 a

b

b

c

c

∫ ydx

∫ ydx

a

a

23

7.ОПОРНЫЕ ЗАДАЧИ

7.1.Вычислить интегралы:

					3																	7				dt
	1)					∫3x2dx																3) ∫
																										3t + 4
					2																			−1
																								π
	4									x															2a
		2) ∫(1 + e									)dx											4)			∫ (x + 3)sin axdx
										4
	0																								0
	Решение. Применяя формулу Ньютона-Лейбница и свойство
определённого интеграла, получим:
3					3
1) ∫3x2dx = 3∫x2dx = x3 |32 = 33 − 23 = 19 .
2					2
4			x		4					4			x						x
2) ∫(1 + e				)dx = ∫dx + 4∫e										d		x		= x + 24e		|04 = 4 + 4e − 4 = 4e .
			4										4						4
0					0					0		4
7		dt						1		7		1									2	1					2			8
3) ∫							=			∫ (3t +		4)−					d (3t + 4) =					(3t + 4)		|7−1 =				(5 −1) =			.
															2								2
		3t +
−1					4 3					−1								3							3				3

4) Здесь для нахождения неопределённого интеграла применяем

формулу интегрирования по			частям ∫udv = uv − ∫vdu . Полагая
u = x + 3 , dv = sin axdx, получим du = dx,
v = ∫sin ax dx =	1	∫sin ax d (ax) = −	1	∫cos ax,
	a		a

π

2a

∫( x + 3)sin ax dx =

0

= − x + 3 cos ax + 1
a	a2

7.2. Вычислить интегралы.

∫

2π

a

a

−

x + 3

cos ax

+

1

cos ax dx | a

=

0

2π

=

1

+

3

=

1 + 3a

sin ax |

a

.

a2

a

0

a2

π

5

xdx

ln 3

dx

3

(x

3

+ 1)dx

2

dx

1) ∫

;

2) ∫

;

3) ∫

;

4) ∫

.

x

− e

− x

1 + 3x

x2

0

ln 2 e

1

4 − x2

0

2 + cos x

Решение. 1) Вводим новую переменную интегрирования, полагая

1 + 3x = t .

24

Отсюда находим x =

t 2 -1

,

dx =

2

tdt

и новые пределы интеграла:

t = 1

3

3

1

при x1 = 0, t2 = 4, при x2 = 5 . Подставляя, получим:

5

xdx

2

4

2

2

t3

4

2

64 − 1

∫

=

∫(t

− 1)d =

− t

|1

=

− 4 + 1 = 4.

1 +

9

3

0

3x 9

1

9 3

2) Полагая ex

= t,

имеем x = ln t, dx =

dt

; t

= 2

при

x

= ln 2;

t

= 3

при

2

t

1

1

x2 = ln 3 и

ln 3

dx

3

dt

3

dt

1

t − 1

1

2

1

ln1,5

3

=

=

=

ln

|2

=

ln

− ln

=

.

ln∫2 ex − e− x

∫2 t 2 −

+ 1

4

2

∫2 t(t − t −1 )

1 2 t

2

3

= π

3) Полагая

x = 2sin t,

получим: dx = 2cost dt;

t

= π

при

x

= 1;

t

2

1

6

1

3

при x2 =

3;

π

π

π

3

(x3

+1)dx

3

8sin3 t +1

3

1

3

dt

∫

= ∫

dt

= 2∫sin t dt +

∫

=

4sin

2

t

4

sin

2

t

x2

4 - x2

1

π

π

π

6

6

6

π

1

1

3

1

3

7

= -2cost -

ctg t |π3 = -2

-

-

-

3

=

-1.

4

2

2

4

3

2 3

6

4) Заменяя

переменную

при

помощи

подстановки

tg

x

= z,

найдём

2

cos x =

1 − z2

;

dx =

2dz

;

z

= 0 при x

= 0;

z

= 1 при

x

= π

и

1 + z2

1 + z2

1

1

2

2

2

π

π

π

2

dx

1

dz

2

z

2

∫0

= 2∫0

=

arctg

|10 =

× 6

=

.

2 + cos x

z2 + 3

3

3

3

3

3

7.3. Найти площадь фигуры,

ограниченной осью Ox и графиком

функции y = x2 - 2x при x [0;3].

Решение.

Графиком

функции

y = x2 - 2x

является

парабола,

поэтому фигура имеет вид, изображённый на рисунке 14.

25

y

y=x2

0	2	3	x

Рис. 14.

Её площадь равна

	2						3
	S = −∫(x2 − 2x)dx + ∫(x2 − 2x)dx =
	0						2
	= −	x3		2 + x2		2 +		x3			3 − x2		3 = −	8	+ 4 +	27	−	8	− 9 + 4 =	8	.
																3
	3			0		0	3				2		2	3			3			3

7.4. Вычислить площадь, ограниченную следующими линиями: параболой 4 y = 8x − x2 и прямой 4 y = x + 6 .

			Рис. 15.
Решение. Совместно решая данные							уравнения, определим								две
															7
точки пересечения линий, ограничивающих искомую площадь, A 1;																,
															4
B(6;3) . Построив эти точки и проходящие через них данные линии
(рис. 15), видим, что		искомая	площадь				равна					разности площадей
S1 = A1 ANBB1 и S2 = A1 ANBB1 . Площадь S1 выражается интегралом
6		6							3
S1 = ∫ y dx =	1	∫(8x - x2 )dx =		1		2		x			16	=	205	.
					4x		-
1	4	1		4				3				12

Площадь S2 трапеции А1 АВВ1 равна произведению полусуммы её оснований на высоту:

26

S	2	=	A1 A + B1B	× A B =		95	.
		2		1	1	8

Следовательно, искомая площадь S = S - S				=	205		-	95		= 5	5	.
			2
		1		12					8	24
Если за единицу длины принят дециметр, то S = 5						5			кв.дм.
				24
7.5.	Вычислить	площадь фигуры,			ограниченной эллипсом
x = cost ,	y = sin t .
Решение. Найдём сначала 1/ 4 площади S . Здесь x изменяется от
0 до a , следовательно, t		изменяется от π / 2 до 0 (рис. 16). Находим

Рис. 16

		1				0						0		ab	0
				S =			∫ bsin t × (-a sin t)dt = -ab ∫						sin2 tdt =		∫ (1 - cos 2t)dt
	4					π / 2						π / 2	2		π / 2
			ab					π0 / 2 -	1			/ 2 ) = π ab . Таким образом S = 4 × π ab = π ab .
	=				(t					sin 2t	π0
	2							2				4			4

7.6. Вычислить площадь фигуры, ограниченной r = a cos3ϕ . Решение. Найдём сначала площадь половины одного лепестка

«розы» (рис.17), т.е. 1/6 часть всей площади фигуры.

Рис. 17.

27

	1				1		π / 6							1				π / 6	1
		S =						∫ (a cos3ϕ)2dϕ =								a2		∫		(1 + cos 6ϕ)dϕ =
	6																		2
				2		0					2							0
	=		a2	(ϕ				π0 / 6 +	1	sin 6ϕ			π0 / 6 ) =		a2			(π + 0) = π a2			. S = 6 × π a2	= π a2 .
	4							6					4					6	24		24		4
					7.7. Найти длину окружности радиуса R .
					Решение.						Найдём 1 / 4 часть её длины от точки												(0;R) до точки

(R;0) . Так как уравнение окружности в декартовой системе координат

			1	R		x2			x
y =	R2 - x2	, то		l = ∫ 1 +				dx = R arcsin
					R	2	2		R
4				0		- x

Длина окружности l = 4 × R × π = 2π R . 2

R

0

= R × π .

2

Если уравнение окружности записать в параметрическом виде

2π

x = R cost , y = R sin t , то l = ∫ 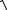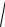(-R sin t)2 + (R cost)2 dt = Rt 02π = 2π R .

0

7.8. Найти длину кардиоиды r = a(1 + cosϕ) .

Решение. Кардиоида симметрична относительно полярной оси

(рис.18).

				Рис. 18
	Найдём половину длины кардиоиды
		1	π		π
			l = ∫	(a(1 + cosϕ))2 + (a(-sinϕ))2	dϕ = a∫		dϕ =
						2 + 2cosϕ
	2
			0	0

28

π				π
= a∫		2 × 2cos2 ϕ dϕ = 2a∫cos			ϕ dϕ = 4a sin ϕ			π0 = 4a .
0	2			0	2	2
Отсюда l = 2 × 4a = 8a .
	7.9. Найти			объём тела,		образованного вращением фигуры,

ограниченной линиями y = x2 , x = 0 , y = 22 вокруг оси Oy (рис. 19).

2

Рис. 19

b

Решение. По формуле Vy = π ∫ x2dy , где x = ϕ ( y) ³ 0 , находим

a

2

2

Vy = π ∫

2 ydy = π y

2

2

2

= 8π .

0

0

x2

+

y2

+

z2

= 1.

7.10. Найти объём эллипсоида

a2

b2

c2

Решение. Рассекая эллипсоид плоскостью, параллельной

плоскости Oyz на расстоянии

x от неё (-a £ x £ a) получим эллипс

(рис. 20)

y2

+

z2

=1.

(b 1 -

x2

)2

(c 1 -

x2

)2

a2

a2

29

Рис. 20

Площадь этого эллипса равна S (x) = π bc(1 −

x2

) .

a2

b

0

x

2

4

Поэтому, по формуле V = ∫ S (x)dx имеем V = π bc ∫

(1 −

)dx =

π abc .

a

2

a

−a

3

7.11. Найти объём трёхосного эллипсоида

x2

+

y2

+

z2

= 1.

a2

c2

b2

Рис. 21

Решение. Плоское сечение эллипсоида, параллельное плоскости xOz и отстоящее от неё на расстоянии y = h (рис. 21), представляет

x2

+

z2

= 1 −

y2

x2

+

z2

= 1

a =

a

;

эллипс

,

с полуосями

b2 − h2

a2

c2

b2

a2

c2

1

b

c =

c

. Площадь этого сечения, как площадь эллипса, найдём по

b2 − h2

1

b

формуле S (h) = π a c = π ac

(b2 − h2 ) .

1 1

b2

b

Подставляя

в

формулу

V = ∫ S (x)dx ,

получим

объём всего

a

π ac b

2π ac

h3

4

эллипсоида

V = b2

∫(b2 − h2 )dh =

(b2h −

) |b0 =

π abc .

b2

3

3

0

30