oin

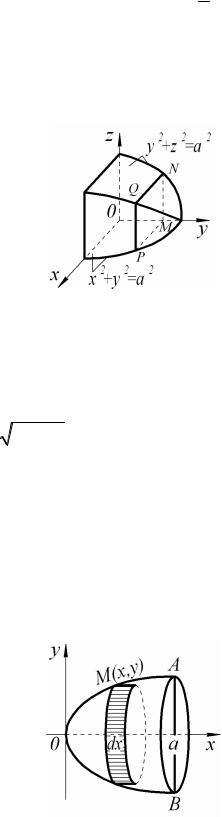
При a = b = c полученная формула для объёма эллипсоида

преобразуется в формулу для объёма шара V = 4 π a3 . 3

7.12. Найти объём, общий двум цилиндрам: x2 + y2 = a2 и y2 + z2 = a2 , ограниченный данными цилиндрическими поверхностями.

Рис. 22

Решение. Построим восьмую часть тела, расположенную в первом октанте, рис. 22.

Любое сечение тела плоскостью, параллельной плоскости xOz , представляет квадрат. Площадь сечения PQNM, отстоящего от плоскости xOz на расстоянии OM = h , найдём как площадь квадрата со

				S (h) = a2 − h2 ,0 ≤ h ≤ a. Весь искомый
	стороной MP = MN = a2 − h2 ;
		b
	объём, согласно формуле V = ∫S ( x)dx , выразится интегралом
		a
	V = 8∫a (a2 − h2 )dh = 8 a2h −				h3	|0a =	16	a3 .
					3		3
	0

7.13. Вычислить объём тела, образованного вращением фигуры, ограниченной линиями: 1) y2 = 2 px , x = a вокруг оси Ox .

Рис. 23

31

Решение. 1) Построив параболу y2 = 2 px и прямую x = a ,

получим параболический сегмент OAB , рис.23. При вращении его вокруг оси образуется сегмент параболоида вращения. Объём этого тела, согласно общим указаниям, найдём по формуле:

x2

a

V = π ∫y2dx = π ∫2 px dx = π px2 |0a = π pa2 .

x1 0

7.14.

Вычислить длину

дуги

1) полукубической

параболы

y2 = (x -1)3

между точками A(2;-1) и B (5; -8).

Решение. Разрешаем

данное

уравнение

относительно y и

найдём y¢ :

3

3

1

y = ±(x -1)

, y '= ±

(x - 1)

. (Знаки ± в выражении y указывают,

2

2

2

Ox ; точки

A и B ,

что кривая симметрична

оси

имеющие

отрицательные ординаты, лежат на той ветви кривой, которая расположена ниже оси Ox .)

				xB							5			9
	LAB = ∫					1 + ( y')2 dx = ∫						1 +			( x -1)dx =
				xA							2	4
		1	5						1	5		1								1	3
	=		∫				dx =			∫						)		d (9x - 5) =			(9x - 5)		|5
					9x - 5						(	9x - 5												»7,63 .
																	2					2
	2					18														27			2
			2							2

7.15. Найти площадь поверхности шара радиуса R .

Решение. Можно считать, что поверхность шара образована

вращением полуокружности

y = R2 − x2 , -R £ x £ R вокруг оси Ox .

b

По формуле

Sx = 2π ∫ y ×

1 + ( y¢)2

dx ,

где

y = f (x) ³ 0 – кривая,

a

вращающаяся вокруг оси Ox , находим

R

-x

2

R

S = 2π ∫

R2 - x2 × 1 +

dx = 2π ∫

R2 - x2 + x2

dx =

R2 - x2

− R

− R

= 2π R × x −RR = 4π R2 .

32

7.16. Какую работу нужно затратить, чтобы растянуть пружину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м?

Решение. По закону Гука упругая сила, растягивающая пружину,

пропорциональна этому	растяжению		x , т.	е.		F = kx , где				k –
коэффициент пропорциональности.		Согласно		условию задачи,						сила
F = 100Н растягивает	пружину	на	x = 0,01м,						следовательно,
100 = k × 0,01, откуда k = 1000 , следовательно, F = 1000x .
	0,05
Искомая работа равна A = ∫ 10000xdx = 5000x					2			0,05	= 12,5( Дж) .
								0
	0
7.17. Найти путь, пройденный телом за 4 секунды от начала
движения, если скорость тела v(t) = 10t + 2 (м/c).
Решение. Если v(t) = 10t + 2 (м/с), то путь,				пройденный телом от

начала движения ( t = 0 ) до конца 4-й секунды, равен

4

S = ∫(10t + 2)dt = (5t 2 + 2t) 04 = 88( м) .

0

7.18. Определить давление воды на вертикальный прямоугольный шлюз с основанием 18 м и высотой 6 м.

	Рис. 24
Решение. Величина p давления		жидкости	на	горизонтальную
площадку зависит от глубины её погружения x ,			т. е.		от расстояния
площадки до	поверхности жидкости:	p = δ ax ;	δ	–	удельный	вес
жидкости, a −	площадь площадки.
Руководствуясь общей схемой II применения определённого
интеграла к	исчислению величин, разделим шлюз				на глубине	x

33

горизонтальной прямой. Тогда давление воды на верхнюю часть шлюза будет некоторой функцией p(x) . Найдём дифференциал dp этой

функции, т. е. приближённую величину (главную часть) её приращения p при изменении глубины x , на малую величинуdx . Допустим, ввиду

малости dx , что все точки заштрихованной полоски находятся на глубине x , т. е. что она расположена на глубине x в горизонтальной плоскости. Тогда приближенная величина давления воды на эту полоску будет равна весу столба воды, имеющего основанием эту полоску, и

высотой −	глубину	x :	p ≈ dp = 18δ xdx = 18xdx (удельный вес воды
δ = 1). Согласно условию			задачи глубина	x	изменяется на	отрезке
0 ≤ x ≤ 6 .	Поэтому	искомое давление P		на	весь шлюз	найдём,

интегрируя dp в пределах от 0 до 6:

6

P =18∫x dx = 9x2 |60 = 324T » 324000 ×9,81н » 3178440н » 3,18Мн.

0

7.19. Вычислить работу, необходимую для выкачивания масла из вертикального цилиндрического резервуара высотой H=6 м. и радиусом основания R=1 м. Удельный вес масла δ = 0.9 .

Решение. Величина работы q , затрачиваемой на поднятие некоторого тела, зависит от высоты x его подъёма: q = Px , P − вес

тела.

Допустим, что работа, затраченная на выкачивание из резервуара слоя масла толщиною x , рис. 25, есть некоторая функция q(x) и найдём

дифференциал этой функции.

Рис. 25

34

При увеличении x на величину dx объем v слоя масла

увеличится на величину

v = π R2dx , его вес

p увеличится на величину

p = π R2dx , а

затраченная

работа

q

увеличится на

величину

q ≈ πδ R2 xdx = dq .

Всю искомую работу Q получим при изменении x

от 0 до H.

Поэтому

|0H = πδ R

H

≈ 64800π ≈ 64800 * 9.81π (дж)

Q = πδ R2 ∫xdx = πδ R2 x

2

H

2

2

0

2

2

≈ 635688π (дж).

7.20. Найти следующие несобственные интегралы:

+∞

+∞

dx

1

dx

2

dx

1) ∫e− x dx; 2) ∫

; 3)

∫

; 4)

∫

.

2

3 (x −1)2

0

−∞ x

+ 1

0

x

−1

Решение.

β

+∞

(−e− x ) |0β = lim(e0 − e− β ) = 1.

1) ∫e− xdx = βlim→+∞ ∫e− xdx = lim

0

0

Следовательно, данный несобственный интеграл сходится.

Геометрически,

в прямоугольной

системе

координат, всякий

a

определённый интеграл ∫ f (x)dx даёт алгебраическую сумму площадей,

b

ограниченных кривой y = f (x) , двумя вертикальными прямыми x = a , x = b и осью Ox . Поэтому, построив кривую y = e− x и её ординаты в точках x = 0 и x = β (рис. 26), получим криволинейную трапецию

β

0ABβ , площадь которой S (β ) = ∫e− x dx = 1 − e− β .

0

При β → ∞ получим трапецию с бесконечным основанием,

которая имеет конечную площадь S (= ∞) = lim S (β ) = 1.

β →∞

Рис. 26

35

1)

Пользуясь определением, получим

+∞

dx

0

dx

β

dx

= lim arctg x |α0 + lim arctgx |0β =

−∞∫

αlim→−∞ α∫

+ βlim→+∞ ∫0

=

x2 + 1

x2 + 1

x2 + 1

= −arctg (

−

π

π

= π .

−∞) + arctg (+∞) = −

2

+

2

Рис. 27
	1
Геометрически (рис. 27) интеграл от функции	f ( x) =		в
		x2 + 1

пределах от α до β выражает площадь криволинейной трапеции α ABβ , а данный несобственный сходящийся интеграл выражает площадь бесконечной криволинейной трапеции, которая неограниченно простирается влево и вправо и вместе с тем имеет конечную величину π .

	3) Здесь при	x = 0 подынтегральная функция					1	имеет бесконечный
							x
	разрыв. Согласно определению
	1	dx	= lim	1	dx	= lim ln x |1ε = lim (ln1 − ln ε ) = − ln 0 = +∞,
	∫0
		x ε →+0		∫ε x

т.е. этот несобственный интеграл расходится.

Геометрически (рис.28) полученный результат указывает, что площадь криволинейной трапеции ε ABβ

1

S (ε ) = ∫ dx = − ln ε

ε x

При ε → +0 неограниченно возрастает.

36

Рис. 28

4) Здесь подынтегральная функция имеет бесконечный разрыв в точке x = 1, лежащей внутри отрезка интегрирования [−1;2] . Согласно

определению

2

dx

1−ε1

dx

2

dx

∫

= lim

∫

+ lim

∫

=

−1

3 (x −

1)2

ε1 →+0

−1

3 (x

−1)2

ε

2 →+0

1+ε2

3 (x −1)2

= lim33

|1−−1ε1 + lim33

|12+ε1

= 3lim

( 3

− 3

) +

x −1

x −1

−ε1

−2

+3lim ( 3

− 3

) = 3( 3

+ 1).

1

ε2

2

Для графика подынтегральной функции

y =

1

(рис.29)

прямая

3 (x −1)2

x = 1 является вертикальной асимптотой.

Рис. 29

Интегралы от этой функции в пределах от −1 до 1 − ε1 и от 1+ ε2 до 2 выражают площади криволинейных трапеций α APε и nQBβ . При ε1 → +0 и ε 2 → +0 эти трапеции неограниченно простираются вверх и

вместе с тем имеют конечные площади, сумма которых равна найденному значению данного несобственного сходящегося интеграла.

37

8. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Вычислить интегралы:

5

dx

8.1.

(ЭГГ) ∫

;

1

3x − 2

1

dz

8.2.

(ФЖШ) ∫

;

(2z + 1)3

0

2

dt

8.3.

(ЛПБ) ∫

;

t 2 + 5t + 4

1

2

x + 3

8.4.

(ЖМД) ∫

dx

;

x2

+ 4

0

a

x

8.5.

(ЮШМ) ∫ x cos

dx ;

−a

2

π

x

3x

8.6.

(ЮМФ) ∫cos

cos

dx ;

2

0

2

π

8.7.

*(ЮШБ) ∫ x sin x cos xdx ;

−π

e

8.8.(КБД) ∫(1 + ln y)2 dy ;

1

1

x2dx

8.9. (ДБА) ∫

подстановка x + 1

= z ;

(x + 1)4

0

ln 2

= t.

8.10. (ПКФ) ∫

ex − 1

dx подстановка

ex −1

0

7

x3dx

8.11. (ЦЮЦ) ∫

подстановка z = x2

+ 1;

3 (x2 + 1)2

3

3

8.12. (ЛЖФ) ∫x2 9 − x2 dx подстановка x = 3cosϕ ;

−3

1

8.13. (КФЭ) ∫ tdt ;

5 5 + 4t

π

4 1 + tg 2ϕ

8.14. (БМС) ∫ dϕ ;

0 1 + tgϕ

38

0

1 − ex

8.15. (ФЮГ) ∫

dx

1 + ex

ln 3

0

dx

8.16. (АМИ) ∫

;

3

1 +

x

+ 1

−1

3

x

8.17. *(ФКШ) ∫

dx подстановка x = 6sin2 t *;

0

6 − x

π

2

8.18. *(ФЦГ) ∫sin3 ϕ

cosϕ

dϕ ;

0

1

8.19. (ГАС) ∫ ex dx ;

−∞

+∞

dx

8.20. (ЦМЦ) ∫

;

x2

+ 2x + 2

−∞

1

8.21. (МСЖ) ∫ln x dx ;

0

0

8.22. (ДИЛ) ∫ xex dx .

−∞

8.23.Вычислить площадь фигуры, ограниченной линиями (ответ записать в виде обыкновенной дроби, если полученное значение не целое):

а) (ААГ) y = x2 − 6 и y = −x2 + 5x − 6 ;	б) (ЛСГ)	y = x2 , y = 2x и y = x ;
в) (КИЮ) 4 y = 8x − x2 и 4 y = x + 6 ;	г) (ПБЮ)	y = x3 − 3x и y = x ;
д) (ЛЦЛ) y = 4 − x2 и y = x2 − 2x ;
е) (МЮИ) 6x = y3 −16 y и 24x = y3 −16 y .

8.24.Найти объём тела, образованного вращением фигуры, ограниченной линиями:

а) (ЦКИ) y = sin x , y = 0 вокруг оси Ox ;

б) (ИСИ) y2 + x − 4 = 0 , x = 0 вокруг оси Oy . 8.25. Вычислить длину дуги кривой:

а) (КЛД) 9 y2 = 4(3 − x)3 между точками пересечения с осью Oy ; б) (ЛШЦ) астроиды x = a cos3 t , y = a sin3 t ;

в) (МГМ) кардиоиды ρ = a(1 + cosϕ .

39

9. ПРОВЕРЬТЕ СЕБЯ Вариант 1

ЗАДАНИЯ

ВАРИАНТЫ ОТВЕТОВ

2

А) 7,6

Б) 6,5

1. (БКС) ∫ x4 dx равен

В) 7,2

Г) 6,6

−1

π

11

А) 11

Б) 22

2. (АШИ) ∫

dx равен

В) 0

Г) -11

cos

2

0

x

3. (ФШЮ)

Вычисление несобственного

А) интеграл расходится

Б) π 2

+∞

dx

В) π

Г) 0

интеграла

∫

приводит к

x2

+ 2x + 2

−∞

следующему результату

1

2x2 − 2x − 7 dx равен

А) − 26 3

4. (АПШ)

∫(

Б) 19 3

)

В) 23 3

Г) − 22 3

0

5. (БЮГ)

Какое из утверждений верно?

А) функция от x

5

Б) функция от

f ( x)

Интеграл ∫( f ( x) − ϕ( x))dx –

это:

В) функция от y = f ( x) − ϕ( x)

3

Г) число

Вариант 2

ЗАДАНИЯ

ВАРИАНТЫ ОТВЕТОВ

π

А) 2

Б) 1

1.

(АЭШ)

Значение интеграла

∫sin2 xdx

В)

π

Г) π

0

2

равно

0

А) −

e

2

2.

(ДЭЭ)

Значение интеграла

∫ xex dx

Б) −e

2

равно

−1

1− e

2 − e

В)

Г)

2

2

3. (АГИ) Каков геометрический смысл

А) длина линии y = f ( x) в интервале

определенного интеграла от функции

[a;b]

y = f ( x)

в интервале [a;b]

в системе

Б)

площадь

фигуры,

ограниченной

декартовых координат

линией y = f ( x) в интервале [a;b]

В) среднее значение функции y = f ( x)

в интервале [a;b]

Г)

максимальное значение функции

y = f ( x) в интервале [a;b]

4. (БЛК)

Вычисление несобственного

А) интеграл расходится

+∞

Б) I = 0

интеграла

I = ∫ xe−2 x dx

приводит к

0

40