§3. Проекция вектора на ось. Координаты вектора. Компоненты вектора.

1. Проекция вектора на ось.

П

усть векторлежит на некоторой оси. Направление ортасоответствует направлению оси (Рис. 2.3.1).

Рис. 2.3.2

Рис. 2.3.1

Определение 1. Проекцией вектора, лежащего на оси, на эту ось называется число, по абсолютной величине равное длине вектора и взятое со знаком плюс, если направление вектора совпадает с направлением оси и со знаком минус, если они противоположны.

Пусть вектор не лежит на оси. Из точек и опустим перпендикуляры на ось. Получим соответственно две точкии. (Рис. 2.3.2). Векторназываетсякомпонентой векторапо оси.

Определение 2. Проекцией вектора, не лежащего на оси, на эту ось называется проекция его компоненты по осина эту же ось. Проекция вектора на ось обычно обозначается так:. Очевидно, если векторлежит на оси, то можно написать:

Замечание. Отметим, что проекция вектора на осьявляется также координатой векторапо этой оси.

2. Компоненты вектора по координатным осям и координаты точки.

Поместим начало вектора aв начало декартовой системы координатOxyz(его конец – точка).

Спроектируем точку на координатные оси. Получим соответственно три точки,,(рис. 2.3.3).

Как было отмечено, векторы ,,, лежащие на координатных осяхOx.OyиOz, являются компонентами векторапо координатным осям. Обозначим через,и- проекции вектораaна координатные оси. Ясно, что,,, т.к.

=, то.

Такое представление вектора называется разложением его накомпоненты, илисоставляющиепо координатным осям. Нетрудно заметить, что векторлежит на диагонали параллелепипеда, следовательно, можно найти его длину, т.е..

Проекции вектора на координатные оси, т.е. числа,и, являются координатами вектораи записываются так:или.

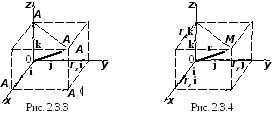
Рассмотрим теперь некоторую точку в пространстве. Векторназывается радиус-вектором точки (рис 2.3.4). Проекции,,радиус-вектора точкина координатные оси называются координатами точкив данной системе координат, и при этом их обозначают простои, т.е. точкаимеет координатыизаписывают так:.

§ 4 Теоремы о проекциях вектора.

Определение 1. Углом между вектором и осьюназывается наименьший угол между направлением вектораи положительным направлением оси , обозначается.

Теорема 1.Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью.

Доказательство. Пусть уголострый, тогда. Если жетупой (рис. 2.4.1), то ясно, чтопр.

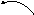
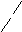
Рис. 2.4.1

Рис. 2.4.2

Замечание (о направляющих косинусах вектора).

Косинусы углов ,и, которые векторобразует с координатными осямиOx, Oy иOz, называются направляющими косинусами вектораa (Рис.2.4.2). Если,,проекции векторана координатные оси, то ясно, что имеют место формулы

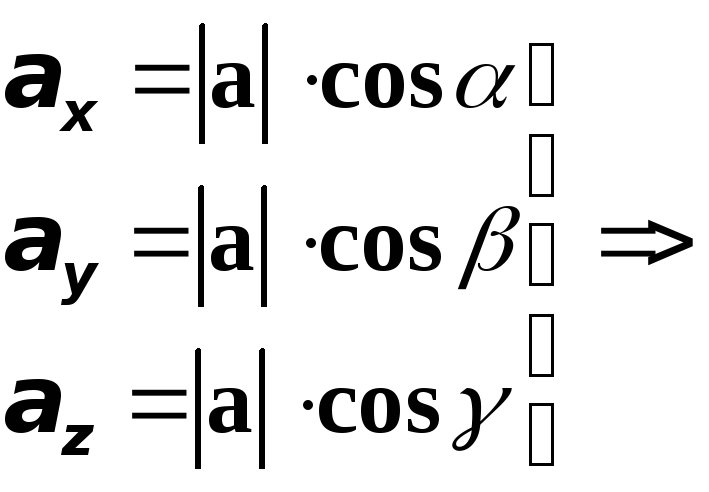
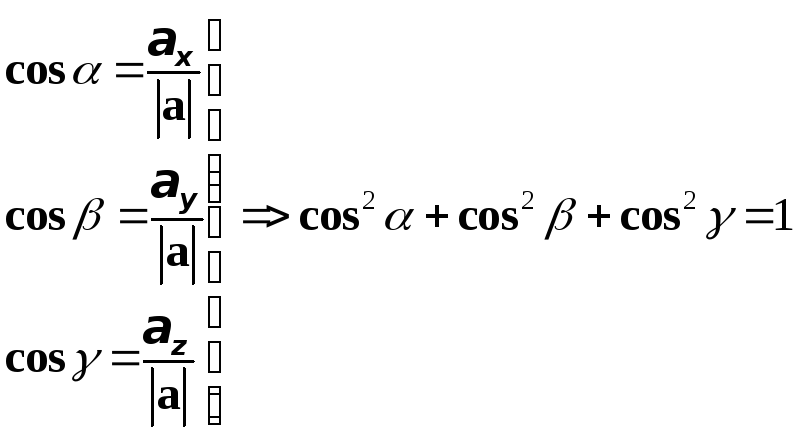
Рис. 2.4.3

Рис. 2.4.4

Теорема 2.Проекция суммы векторов на ось равна сумме проекций этих векторов на эту же ось, т.е.прпрпр.

Доказательство.

(1)

пр;пр;пр;

С другой стороны (Рис. 2.4.3),

(2)

прпрпрпр.

Сравнивая правые части равенств (1) и (2), получаем прпр.

Пример 1. Найти координаты вектораи его длину, если известны координаты его началаи конца- (рис . 2.4.4).

Решение.

Проведём радиус-векторы точек A иB:и.

Ясно, что ;

.

Итак, чтобы найти координаты вектора, нужно из координат его конца вычесть соответственно координаты начала.

Мы получили ранее, что если , то. Следовательно,. Заметим, что по этой формуле удобно вычислять расстояние между двумя точками, если известны их координаты.

Теорема 3.При умножении векторана числоего проекция на ось также умножается на это число, т.е.прпр.

(Без доказательства).

Теорема 4.Для того, чтобы два вектора были равны, необходимо и достаточно, чтобы их проекции на любую ось были равны.

(Доказать самостоятельно).

Пример 2. Даны точкиA(1,-1,2) иB(3,2,3) (рис 2.4.5)

Найти: 1. Координаты вектора; 2. Длину вектора; 3. Разложение векторана составляющие; 4.Направляющие косинусы вектора;

5. Единичный вектор (орт), соответствующий вектору .

Решение 1. Принимая во внимание предыдущий пример, получим: ,,. Итак.

2. Напомним, что , значит.

3. Так как , то.

4. Напомним, что ,,, где,,- углы, которые векторсоставляет с координатными осямиOx, Oy,Oz.

Как известно, ,, называютсянаправляющими косинусамивектора. В нашем случае,,.

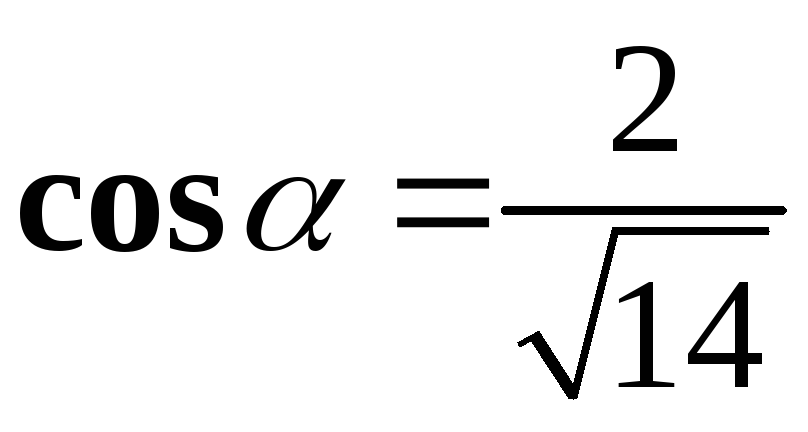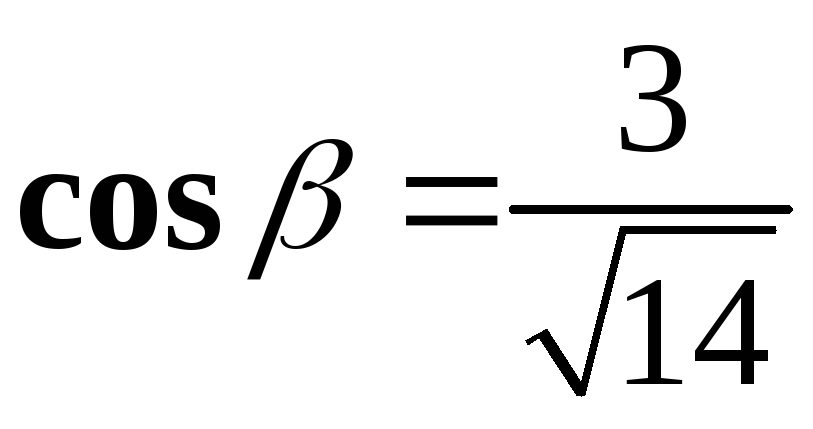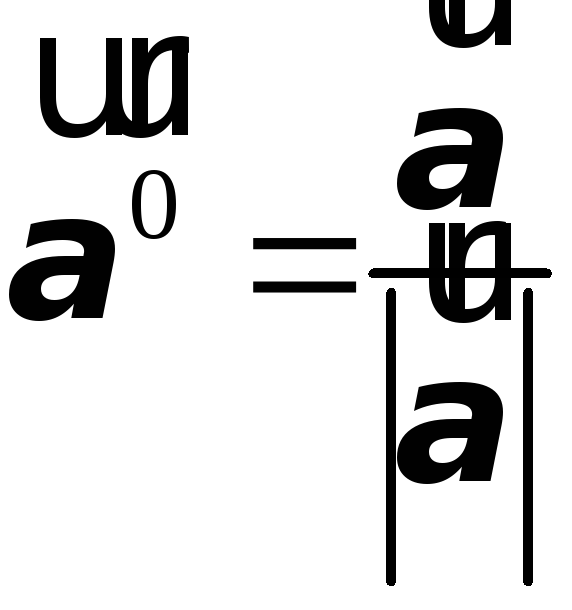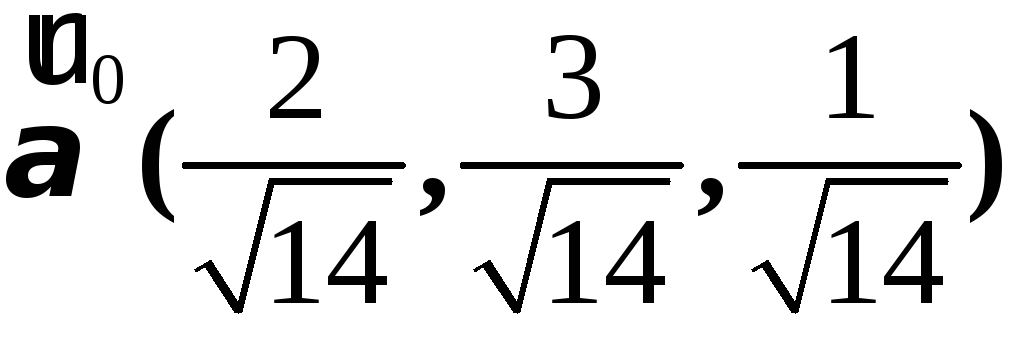5. Единичный вектор , соответствующий вектору, равен. Таким образомили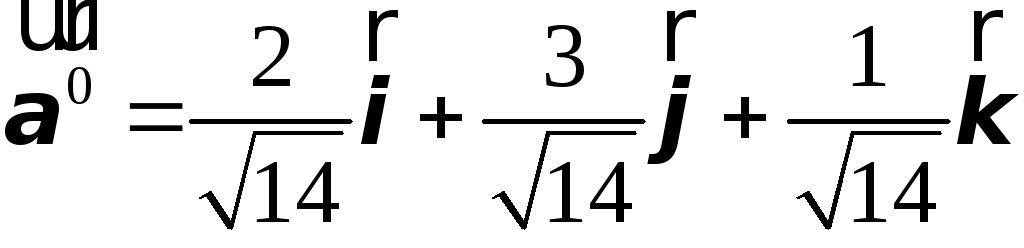. Нетрудно отметить, что координаты единичного вектора совпадают с его направляющими косинусами.

Рис. 2.4.5

Рис. 2.4.6

Пример 3. Дан вектори координаты точек , . Найти координаты вектора. (рис. 2.4.6)

Решение. Найдём координаты вектора.

Итак .

Пример 4.Выяснить, при каких значениях параметровивектораиколлинеарны.

Решение. Напомним, что два вектораиколлинеарны, если они лежат на параллельных прямых или на одной прямой, а тогда, как было отмечено выше, они линейно зависимы. Следовательно, существует некая константаcтакая, что имеет место соотношение.

Откуда следует, что . Значит

.

Так как векторы ,,линейно независимы, ибо они представляют собою базис, то должны обращаться в ноль коэффициенты этой линейной комбинации, т.е.

.

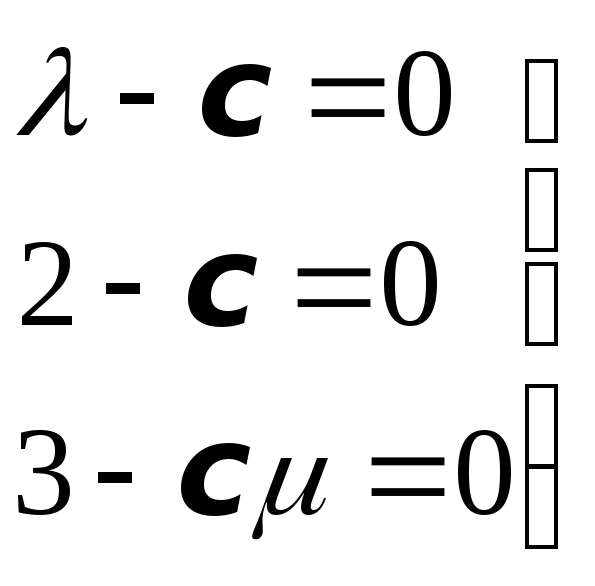Из второго уравнения имеем ; подставляя его в первое и третье уравнения, получим значения интересующих нас констант:,.