При |
сечении |
плоскостью |
x2 0 |
имеем |
параболу |
F x1 3 2 9 . |
|
F 0 |
имеем |
параболу |
При |
сечении |
плоскостью |
x2 x1 3 2 9. |
|
|
|
|
При сечении плоскостью x1 3 имеем прямую F x2 9 .
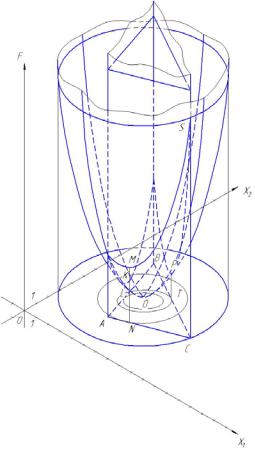
На рис. 21.1 достаточно хорошо видно, что при пересечении наклонного параболического цилиндра (целевой функции F ) с «призматическим» телом (системой ограничений) можно выделить две точки M и P. Они характерны тем, что MN min F и PD max F .
Это качественное решение задачи.
Если параболический цилиндр рассекать координатными плоскостями параллельными плоскости F 0 , то в сечении имеем линии уровня– параболы, параллельные друг другу. Они отличаются только тем, что находятся на разных уровнях F , которые в свою очередь указывают на значение целевой функции F . Сравнивая уровни F точек M и P для соответствующих парабол, можно сделать указанный выше вывод.
Напомним, градиент функции нескольких переменных в какойлибо точке указывает направление наинтенсивнейшего изменения (наибольшего возрастания) функции в этой точке и всегда направлен перпендикулярно линиям уровня. В нашем случае:
|
|
F |
|
F |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
grad F |
i |
|
j |
x2 x1 3 |
9 |
i |
x2 x1 3 |
9 |
j |
x |
x |
|
x |
|
x |
|
|
|
1 |
|
2 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
2 x1 3 i j.
Видно, что вектор grad F находится в плоскости x1Ox2
(параллельных плоскостях). Он меняется и по величине и по направлению в зависимости от изменения x1 . Но есть точка x1, в
котором вектор grad F становится стационарным, т.е. указывает одно и то же направление и величину. Это точка x1 3,при которой grad F j .
Воспользуемся этим обстоятельством для нашей целевой функции F (наклонного параболического цилиндра) и ее линий уровня.
При F С const –общее уравнение линий уровня.
x2 x1 3 2 9 C – общее уравнение парабол-линий уровня
нашей функции.
Видно, что все линии уровняпараболы имеют общее свойство: вершины парабол лежат в плоскости x1 3.
Перемещая вершины парабол (и сами параболы) вдоль плоскости x1 3 по направлению оси Ox2 (на это указывает вектор
grad F j ), мы имеем увеличение целевой функции от F 0 - min F в точке М до max F в точке Р.
Таким образом, решение задачи есть две точки N и D. |
Подставив координаты точек N x1N , x2 N и |
D x1D , x2D в |
формулу для F , находим min F и max F .
Но решение задачи геометрическим методом в объемном ( 3-х мерном) пространстве весьма осложнено построениями. Необходимо, как и прежде, перейти на плоскость, т.е. объемную задачу и ее решение спроектировать на плоскость x1Ox2.
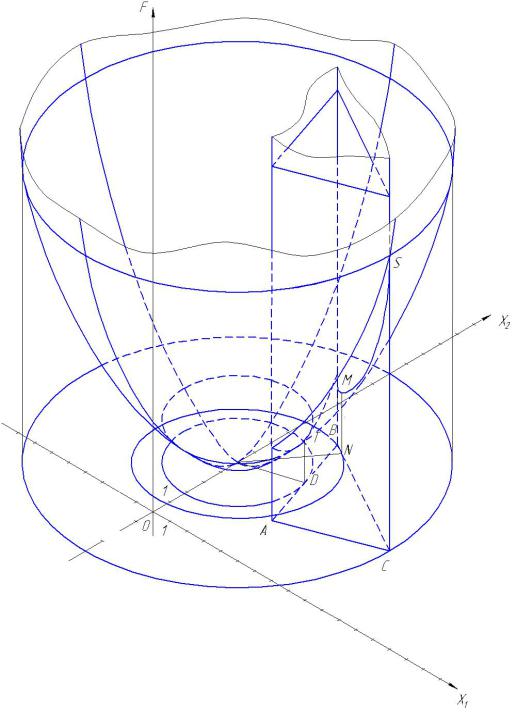
Прямая призма – модель системы ограниченийпроектируется в область допустимых значений( x1, x2 ) виде четырехугольника OABC
(рис. 21.2). Параболылинии уровня параболического цилиндрапроектируются сами на себя, т.к. все они лежат в плоскостях параллельных плоскости x1Ox2 .
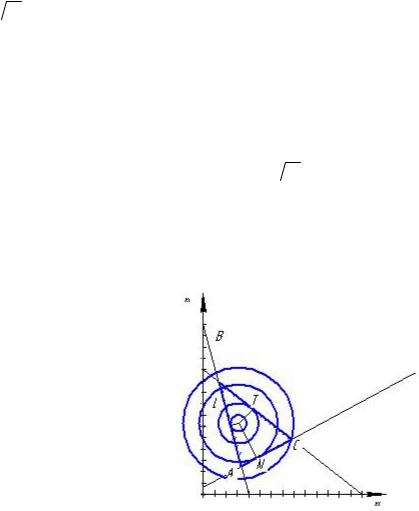
Рисунок 21.2
Перемещение парабол с целью увеличения целевой функции F производится в том же направлении grad F j , т.е. в направлении оси Ox2 , вдоль прямой x1 3 (см. рис.21.2). Решение заключается в
нахождении точек N и D, которые являются точками парабол и граничными точками области допустимых значений одновременно, т.е. это точки касания парабол и граничных прямых четырехугольника
OABC.
Алгоритм геометрического метода решения задачи.
1.Построить область допустимых решений (рис. 21.2).
2.Построить линию уровня целевой функции F (рис. 21.1), приравнивая ее к нулю.
3.Перемещая линию уровня по направлению оси Ox2 вдоль
прямой x1 3 найти граничные точки ( точки касания) линий уровня с границей области допустимых значений.
4.Определить координаты точек, найденных в п.3, которые и будут решением задачи.
5.Найденные координаты точек подставить в формулу (21.1) для F и вычислить min F и max F .
Пример 2. Найти такие значения переменных x1, x2 , при которых обеспечивается максимум (минимум) целевой функции
F x1 |
4 2 |
x2 6 2 , |
(21.3) |
при условиях |
|
|
|
|
|
2x 5x |
7, |
|
|
1 |
|
2 |
|
|
3x1 |
x2 15, |
|
|
|
7x2 |
71, |
(21.4) |
4x1 |
x 0, |
x |
0. |
|
|
1 |
|
2 |
|
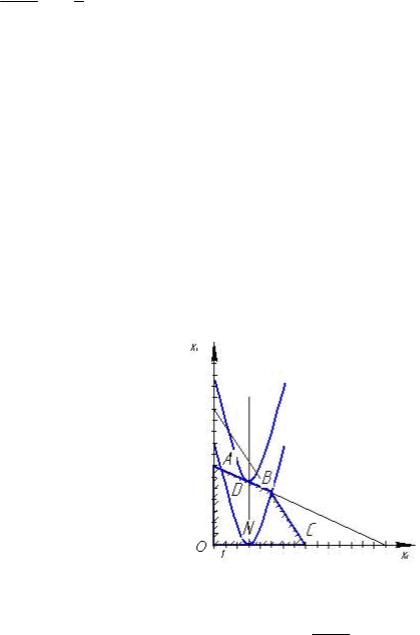
Геометрическая модель системы ограничений в этом примере является тело, ограниченное боковой поверхностью прямой призмы, в сечении которой плоскостью F 0 находится треугольник ABC (рисунок 21.3).
Рисунок 21.3
Геометрическая модель целевой функции F x1 4 2 x2 6 2 представляет собой параболоид вращения, вершина которого находится на плоскости x1Ox2 и смещена на 4 единицы по оси Ox1 и на 6 единиц по оси Ox2 .
Пересечение этих геометрических моделей (рис.21.3) наглядно показывает решение данной задачи квадратического программирования.
В точке О (4,6) имеем min F 0 .
В точке С имеем max F SC . Для вычисления max F необходимо найти координаты точки С и подставить их в формулу (21.3) для целевой функции F .
Таким образом, решение задачи есть координаты точек О и С. Но объемное представление и решение, как это уже показано ранее,
достаточно не простое. |
|
|
на плоскость x1Ox2 и |
Спроектируем |
решение |
задачи |
сформулируем ее алгоритм . |
|
|
Модель системы ограничений, как и прежде, проектируется в |
область допустимых |
значений |
x1, x2 |
в виде треугольника АВС |
(рис.21.4).Линии уровня целевой функцииокружности с радиусом 
F (пересечение поверхности параболоида вращения с плоскостями
|
|
|
|
|
|
|
|
|
|
|
|
F const |
параллельными |
координатной |
плоскости |
F 0 )- |
проектируются |
|
сами |
на |
себя. |
Градиент |
функции |
F |
gradF 2 x1 4 |
|
2 x2 |
6 j - |
вектор |
в плоскостях параллельных |
i |
плоскости |
F 0 - |
указывает |
направление |
увеличения |
целевой |
функции |
F . |
|
Он |
всегда |
перпендикулярен |
линиям |
уровня |
(окружностям) и в данном случае направлен по радиусу от центра.
Радиус этих окружностей равен 
F . Значит, проводя из точки О окружности разных радиусов, можно определить min F 0 (радиус равен нулю) и max F в точке С, т.к. радиус ОС будет самым максимальным в условиях касания области допустимых решений с максимально возможной линией уровня.
Рисунок 21.4
Алгоритм решения задачи.
1.Построить область допустимых решений (рис. 21.4).
2.Построим точку О (4,6)- центр окружностей и с помощью циркуля проведем семейство окружностей с разными радиусами.
3.Точка О есть окружность с радиусом равным нулю или F 0
иявляется решением условия min F 0 .
4.Найдем такую точку, которая одновременно принадлежала бы области допустимых значений и лежала бы на окружности с наибольшим радиусом. Это точка касания указанной окружности с многоугольником допустимых решений. Заметим, что в общем случае касание может произойти как в одной вершине многоугольника, так и с одной из его сторон.
Внашем случае это произошло в точке С.
5.Определить координаты точек, найденных в п.3 и 4, представить их как решение задачи квадратичного программирования, подставить их в формулу (21.3) для F и вычислить min F и max F .
Пример 3. Найти значения переменных x1, x2 , при которых
целевая функция F принимает максимальное и минимальное значение, если
F x2 |
|
x |
2 |
5 2 |
, |
(21.5) |
при условиях |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
5x |
7, |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
3x1 |
x2 15, |
|
(21.6) |
|
|
7x2 |
|
7,1, |
|
4x1 |
|
|
x |
0, |
x |
|
0. |
|
|
1 |
|
|
2 |
|
|
|
|
|
В этом примере граничные условия (21.6) повторяют граничные условия (21.4) предыдущего примера и ,значит, их геометрические модели совпадают.
Геометрическая модель целевой функции |
F x2 |
x |
2 |
5 2 |
|
1 |
|
|
представляет собой такой же параболоид вращения, как и в примере 2, но вершина его смещена только по оси Ox2 на 5 единиц. В результате
вершина параболоида находится за пределами треугольника АВС
(рисунок 21.5).
Рисунок 21.5
Решение задачи в трехмерном пространстве простое. Это точка D, в которой min F TD и точка С, в которой max F SC .
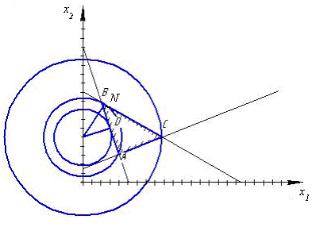
Проектируя данное решение на плоскость (рисунок 21.6), сформулируем алгоритм решения задачи .
356
Рисунок 21.6
1. Построить область допустимых решений (рисунок 21.6).
2. С центром в точке (0;5) построить семейство окружностей и найти такие точки, которые были бы общими и для окружностей с минимальным и максимально возможными радиусами и для треугольника допустимых решений. В нашем случае это точки касания C и D.
3. Определить координаты найденных точек. Эти координаты и есть решения задачи.
4. Определить min F и max F . Для чего подставить значения координат точек решения задачи в формулу (21.5) целевой функции. В нашем случае min F F x1D , x2D , max F F x1C , x2C
21.1.2 Метод множителей Лагранжа
Если в исходной модели математического программирования
(19.1)-(19.3) в системе ограничений (19.2) содержатся только |
равенства, и отсутствует условие (19.3) и f x1, x2 ,..., xn |
и |
gi x1, x2 ,..., xn , |
i 1,2,..., m – функции непрерывные вместе |
со |
своими частными производными, тогда задача |
(19.1)–(19.3) примет |
вид: |
|
|
|
F f x1, x2 ,..., xn max |
, |
(21.7) |
при условии системы ограничений |
|
|
|
gi x1, x2 ,..., xn bi , |
i 1,2,..., m . |
(21.8) |
В курсе математического анализа задачу (21.7)–(21.8) называют задачей на условный экстремум, так как поведение независимых переменных ограничено определенными условиями (21.8).
Эту задачу можно решить методом множителей Лагранжа.
Метод множителей Лагранжа основывается на следующей теореме:
357
Теорема. Пусть точка M 0 является точкой условного экстремума функции F f x1, x2 ,..., xn при выполнении условий (21.8) (уравнений связи). Тогда существуют такие числа 1, 2 ,..., m что в точке M 0 будут выполняться условия
|
F |
g1 |
g2 |
... |
|
gm |
0, |
j 1,2,..., n . |
|
|
x j |
m x j |
|
|
1 x j |
2 x j |
|
|
|
|
Функцией Лагранжа для данной функции F f M называется |
функция вида |
|
|
m |
|
|
|
|
|
|
|
gi x1, x2 ,...,xn . |
|
L x1, x2 ,...,xn , 1,..., m f x1, x2 ,...,xn i bi |
(21.9) |
|
|
|
|
i 1 |
M 0 |
|
|
Из теоремы следует, что |
если |
точка |
является |
точкой |
условного экстремума функции |
F f x1, x2 ,..., xn , то она является |
стационарной точкой для функции Лагранжа, то есть должны выполняться следующие равенства
|
L |
0, |
j 1,2,.., n, |
|
|
|
|
|
|
|
|
xj |
|
|
(21.10) |
|
L |
|
|
|
|
|
0, |
i 1,2,..., m. |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для отыскания точек условного экстремума следует |
рассмотреть систему |
n m |
уравнений (21.10) относительно |
неизвестных x1, x2 ,..., xn , 1,..., m и решить |
ее. Всякое |
решение |
системы уравнений (21.10) определяет точку |
X * x* , x* |
,..., x* , |
|
|
|
|
1 |
2 |
n |
которая является подозрительной точкой на локальный условный экстремум. Следовательно, решив систему уравнений (21.10), получим все точки, в которых целевая функция (21.7) может иметь экстремальное значение.
Описанный здесь метод множителей Лагранжа требует нескольких разъяснений и уточнений.
Система ограничений (21.8) очень часто в литературе рассматривается как система уравнений. Если взять (21.8) как систему линейных алгебраических уравнений (СЛАУ), являющуюся совместной и определенной, т.е. имеющую одно единственной
решение, то задача условного экстремума прозвучит так: найти такую |
точку X x1, x2 ,..., xn , которая обеспечивает |
экстремум функции |
F f x1, x2 ,..., xn max min |
при |
условии |
конкретной |
точки |
X 0 x10 , x20 ,..., xn0 . Конечно, |
такая |
задача |
не имеет |
смысла |
(требуется найти точку, которая уже дана).
Поэтому система ограничений (21.8) должна пониматься не как |
система, а как совокупность функций gi x1, x2 ,..., xn bi , |
i 1,2,...,m . |
Система n m уравнений (21.10) с n m неизвестными
требует уточнений. |
|
Предположим, что функция F f M квадратичная, а функции |
gi x1, x2 ,..., xn bi , |
i 1,2,...,m - линейные (типичный случай |
квадратичного программирования).
Система (21.10) предполагает наличие частных производных,
|
приравненных к нулю: |
L |
0, |
j 1,2,.., n, |
L |
0, i 1,2,..., m . |
|
x j |
i |
|
|
|
|
|
При дифференцировании вторая степень снижается на единицу. Иными словами, система (21.10) становится линейной.
Если СЛАУ совместная и определеннаярешение одно единственное, точка экстремума одна.
Если СЛАУ совместная и неопределеннаярешение составляет бесконечное множество точек. Тогда бесконечное множество экстремумов целевой функцииабсурд.
Вместе с тем, в задачах с условным экстремумом квадратичных функций ( это будет показано ниже) встречаются два, три, т.е. ограниченное число условных экстремумов. Это требует от СЛАУ ограниченное число решений (>1), что также является невозможным. Для этого в системе уравнений ( 21.10 ) должно быть хотя бы одно квадратичное, кубическое и т.д. уравнение.
Чтобы избежать такого казуса с функцией Лагранжа и системой (21.10), предлагается их несколько упростить.
m |
|
В функции Лагранжа (21.9) изъять обозначение . |
|
j 1 |
|
Тогда |
|
Li x1,x2,...x,n, i f x1,x2,...x,n i bi gi x1,x2,...x,n , i 1,2,...m, |
(21.11) |
Формируется функция Лагранжа для одного любого (или каждого) из m условий совокупности функцийограничений (21.8). Всего таких функций будет m.
Система уравнений (21.10) для каждой из функций Лагранжа принимает вид:
Li |
0, |
j 1,2,.., n, |
|
|
xj |
|
|
|
|
|
|
(21.12) |
|
Li |
|
|
|
0. |
|
|
|
i |
|
|
|
|
|
|
|
|
|
Эта система имеет n 1 уравнений с |
n 1 неизвестными |
x1, x2 ,..., xn , i . Например, если |
f x1 , x2 ,..., xn - квадратичная функция, |
то (21.12) есть СЛАУ. Совместная и определенная СЛАУ дает в
решении точку |
X * x* , x* ,..., x* , подозрительную на локальный |
|
1 2 |
n |
условный экстремум. Перебрав индекс i от 1 до m, получим m вариантов функции Лагранжа (21.11) и m систем уравнений (21.12).
Иными словами, производится исследование на условный экстремум для каждого из m условий (21.8).
Лучше несколько раз решать простую задачу, чем один раз сложную.
Но не каждое условие (21.8) дает решение на условный экстремум. Чтобы избежать ненужных излишних вычислений можно воспользоваться геометрическим методом решения задачи квадратичного программирования, который поможет убрать те из условий (21.8), в которых условного экстремума или нет или он не востребован. Геометрически это выражается в ситуации, когда проекция лини уровня не имеет касания с прямой, отражающей одно из условий (21.8). Тогда именно это условие становится лишним в исследованиях. Когда указанное касание имеет место, то условие ограничения, соответствующее этой прямой, можно включить в список исследований.. Но среди этих условных экстремумов могут оказаться такие, которые не востребованы самой задачей математического программирования
Замечание. Касание линии уровня с прямой не нужно путать с касанием этой линии с концом отрезка или с вершиной многоугольника.
Приведем несколько примеров.
На рисунке 21.1, где пример 1 решается геометрическим методом, в трехмерном пространстве отчетливо видно, что min F MN , max F PD , то есть точки N и D являются решением задачи. На рисунке 21.2 этот же пример 1 решается в двухмерном пространстве (на плоскости). Для отыскания точек N и D нужно было найти точки касания проекций линий уровня поверхности F (парабол) с границей области допустимых значений (четырехугольник
OABC).
Если вернуться к рисунку 21.1, то найденные точки N и D можно прокомментировать следующим образом. Точка N является
|
|
|
|
|
|
|
|
|
экстремальной точкой (max) для |
функции |
F x |
2 |
x2 6x |
|
при |
условии x2 0. Действительно, |
|
|
|
1 |
1 |
|
если поверхность |
F |
рассечь |
плоскостью x2 0, то в сечении |
линия пересечения (парабола) |
достигает максимума в точке N(3,0) и этот максимум равен отрезку |
MN. В данном случае конкретно для функции |
F и условия |
x2 0 |
имеет место условный максимум. Но для задачи квадратического программирования это будет минимум целевой функции min F .
Рассуждая аналогичным образом, точка D (точка касания
параболы F const |
и отрезка АВ) есть точка условного максимума |
функции F при |
условии x1 2x2 15 . Или при пересечении |
