Математика Сизов 2011

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

КРАСНОЯРСКИЙ ИНСТИТУТ ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА –

ФИЛИАЛ ФГБОУВПО

«ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» в г. Красноярске

Контрольные задания по математике

и

руководство к их решению

Учебное пособие для втузов

Под редакцией Сизова С.Н.

Красноярск КрИДТ ИрГУПС

2011

УДК 517+519 ББК 22.11

К 65

АВТОРЫ:

С.Н. Сизов, А.П. Хоменко, А.И. Свитачев, О.В. Пашковская, Е.А. Галькова, Е.В. Шалагина.

РЕЦЕНЗЕНТЫ:

Я.Н. Нужин, д-р. физ.-мат. наук, профессор кафедры «Математического обеспечения дискретных устройств и систем», институт фундаментальной подготовки Сибирского Федерального Университета.

С.В. Ушанов, канд. техн. наук, профессор, зав. кафедры «Математики и информатики» Сибирского государственного технологического университета.

УДК 517+519 ББК 22.11

К 65

Контрольные задания по математике и руководство к их решению : учеб. пособ. для ВТУЗов. / С.Н. Сизов [и др.] ; под ред. С.Н. Сизова ; КрИЖТ ИрГУПС. - Красноярск : КрИЖТ ИрГУПС, 2011. -

Учебное пособие представляет собой сборник заданий контрольных работ по курсу математики для студентов-заочников, обучающихся по направлению «Технические науки» (550000). Задания сопровождаются краткими теоретическими сведениями и решениями типовых задач и примеров.

Рекомендовано к изданию методическим советом КрИЖТ ИрГУПС

Печатается в авторской редакции

С.Н. Сизов, А.П. Хоменко, А.И. Свитачев, О.В. Пашковская, Е.А. Галькова, Е.В. Шалагина., 2011

Красноярский институт железнодорожного транспорта, 2011

Оглавление
ОГЛАВЛЕНИЕ.....................................................................................................................................	3
..............................................................	6
1. КОМПЛЕКСНЫЕ ЧИСЛА. ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ
1.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ...............................................................................................................	6
1.2. РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ И ЗАДАЧ................................................................................................	14
1.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .....................................................................................................	21
2. ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ...............................................................	23
2.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.............................................................................................................	23
2.2. РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ И ЗАДАЧ................................................................................................	30
2.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .....................................................................................................	36
3. ПРЕДЕЛЫ......................................................................................................................................	38
3.1 КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ..............................................................................................................	38
3.2. ВЫЧИСЛЕНИЕ ТИПОВЫХ ПРЕДЕЛОВ........................................................................................................	43
3.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .....................................................................................................	51
4. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ........................................................................................................	55
4.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.............................................................................................................	55
4.2. РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ.............................................................................................................	59
4.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .....................................................................................................	65
5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ....................................	68
5.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.............................................................................................................	68
5.2. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ И ПРИМЕРОВ................................................................................................	73
5.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .....................................................................................................	78
6. ИССЛЕДОВАНИЕ ФУНКЦИЙ..........................................................................................................	81
6.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.............................................................................................................	81
6.2. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ И ПРИМЕРОВ................................................................................................	86
6.3 ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ ......................................................................................................	93
7. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.......................................................................................	95
7.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.............................................................................................................	95
7.2. РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ И ЗАДАЧ..............................................................................................	102
7.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ ...................................................................................................	111
8. НЕОПРЕДЕЛЕННЫЙ И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛЫ.................................................................	115
8.1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.............................................................................................................	115
8.2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ....................................................................................	126
8.3 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ..............................................................................................................	135
8.4. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ ...................................................................................................	137
9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ..........................................................................................	141
9.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ...........................................................................................................	141
9.2. РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ И ЗАДАЧ. .............................................................................................	149
9.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ ...................................................................................................	157
10. КРАТНЫЕ, КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ. .............................................	161
11. ДВОЙНОЙ ИНТЕГРАЛ...............................................................................................................	163
11.1. ОПРЕДЕЛЕНИЕ................................................................................................................................	163
11.2. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА ................................................................................................	164
11.3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ..............................................................................	167
11.4. ТИПОВЫЕ ПРИМЕРЫ РЕШЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ.........................................................................	169
11.5. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .................................................................................................	172

3

12. ТРОЙНОЙ ИНТЕГРАЛ................................................................................................................	175
12.1. ОПРЕДЕЛЕНИЕ................................................................................................................................	175
12.2. ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА.................................................................................................	175
12.3. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ ..............................................................................	179
12.4. ТИПОВЫЕ ПРИМЕРЫ РЕШЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ .........................................................................	179
12.5. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .................................................................................................	185
13. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ................................................................................................	172
13.1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ I РОДА..................................................................................................	172
13.2. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ II РОДА.................................................................................................	178
14. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ.................................................................................................	203
14.1. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ I РОДА...................................................................................................	203
14.2. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ II РОДА..................................................................................................	214
15. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ.......................................................................................................	226
15.1. ОПЕРАЦИИ I ПОРЯДКА.....................................................................................................................	226
15.2. ОПЕРАЦИИ II ПОРЯДКА....................................................................................................................	230
15.3. ТИПОВЫЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕОРИИ ПОЛЯ.......................................................................	231
15.4. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ ПО ТЕМЕ “ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ” ............................................	236
16. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ОПЕРАЦИОННОЕ
ИСЧИСЛЕНИЕ .................................................................................................................................	239
16.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.........................................................................................................	239
16.2. РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ И ЗАДАЧ............................................................................................	250
16.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .................................................................................................	259
17. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ...............................................................................	262
17.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.........................................................................................................	262
17.2. РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ И ЗАДАЧ............................................................................................	266
17.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .................................................................................................	269
18. РЯДЫ........................................................................................................................................	272
18.1. ЧИСЛОВЫЕ РЯДЫ............................................................................................................................	272
18.2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ................................................................................................................	281
18.3. РЯДЫ ФУРЬЕ И ИНТЕГРАЛЫ ФУРЬЕ...................................................................................................	292
18.4. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .................................................................................................	300
19. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ..........................................................................................	306
19.1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ.........................................................................	306
19.2. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.......................................................	307
19.3. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ И ПРИМЕРОВ............................................................................................	323
19.4. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ...............................................................................................	330
20. ТРАНСПОРТНАЯ ЗАДАЧА..........................................................................................................	332
20.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.........................................................................................................	332
20.2. РЕШЕНИЕ ТИПОВОЙ ЗАДАЧИ ...........................................................................................................	341
20.3. ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ .................................................................................................	347
21. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ......................................................................................	349
21.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.........................................................................................................	349
21.2. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ И ПРИМЕРОВ............................................................................................	363
21.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ .................................................................................................	370
22. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ ................................................................................	372
22.1 КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ..........................................................................................................	372
22.2. РЕШЕНИЕ ТИПОВОЙ ЗАДАЧИ ...........................................................................................................	375
22.3.ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ..................................................................................................	378

4

23. СЛУЧАЙНЫЕ ПРОЦЕССЫ. ЭЛЕМЕНТЫ ТЕОРИИ ИГР..................................................................	380
23.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.........................................................................................................	380
23.2. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ...............................................................................................................	391
23.3. ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ .................................................................................................	395
24. ТЕОРИЯ ВЕРОЯТНОСТЕЙ...........................................................................................................	402
24.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.........................................................................................................	402
24.2. РЕШЕНИЕ ТИПОВЫХ ЗАДАНИЙ...........................................................................................................	411
24.3. ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ»...........................................................	423
25. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.............................................................................................	427
25.1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ..................................................................................................	427
25.2. РЕШЕНИЕ ТИПОВОГО ЗАДАНИЯ .........................................................................................................	442
25.3. ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ «МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»................................................	454
26. КОНТРОЛЬНЫЕ РАБОТЫ..........................................................................................................	461
ПРИЛОЖЕНИЯ................................................................................................................................	464
ЛИТЕРАТУРА..................................................................................................................................	468

5

1.Комплексные числа. Основы линейной алгебры

1.1.Краткие сведения из теории

1.1.1. Некоторые сведения о комплексных числах

Комплексным числом называется число вида z=a+ib

(алгебраическая форма), где i= 1 (мнимая единица), a=Re z-

действительная часть, b=Im z-мнимая часть комплексного числа.

Свойства мнимой единицы: i2 1, i3 i, i4

1.

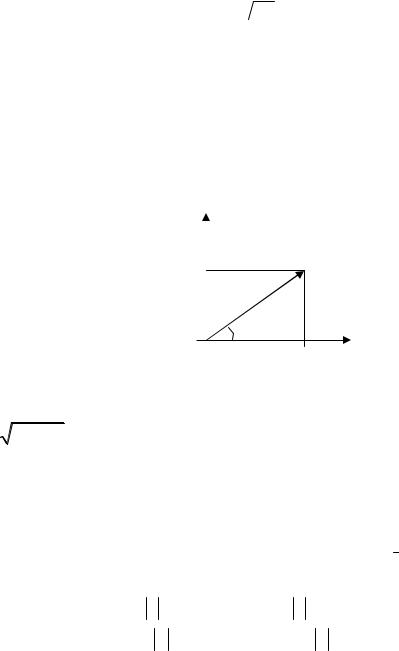
Геометрически комплексное число изображается на плоскости в

виде вектора

z,

имеющего

длину

z

,

называемую модулем

комплексного

числа,

(0

z

),

и направление по отношению к

абсциссе, определяемое углом , который называется аргументом комплексного числа (0 2 )

y

b

z a ib

z

φ

x

a

Перечисленные параметры связаны соотношениями:

z

a2 b2

, arg z arctg b , a Re z

z

cos , b Im z

z

sin .

a

Выражение

z

z

cos isin

есть

тригонометрическая

форма, а

z

z

e j

– показательная

форма

комплексного числа.

Здесь использовалась формула Эйлера: e j cos j sin .

Сопряженным называется комплексное число z , отличающееся знаком мнимой части от комплексного числа z .

Если z a jb z cos j sin z e j , то z a jb z cos j sin z e j .

Действия над комплексными числами

Сложение. Если z1 a1 jb1 , z2 a2 jb2 , то

z1 z2 a1 a2 j b1 b2 .

Следствие: сумма комплексно сопряженных чисел равна удвоенной их действительной части.

6

z z a jb a jb 2a .

Умножение, деление. Если z

z

e j 1 ,

z

2

z

2

e j 2 или

1

1

z

z

( cos j sin ) ,

z2

z2

cos 2

j sin 2 , то

1

1

1

1

z z

2

z

z

2

e j 1 2

z

z

2

cos

2

j sin

2

.

1

1

1

1

1

z

z1

j

z1

cos

j sin

.

1

e

1

2

2

2

z2

z2

z2

1

1

Следствие: произведение комплексно сопряженных чисел равно

квадрату их модуля.

2 .

zz

z

e j

z

e j

z

Умножение и деление можно производить, если комплексные

числа заданы в алгебраической форме:

z1 a1

jb1;z2 a2 jb2 .

z1 z2 a1 jb1 a2 jb2 a1a2 ja1b2 ja2b1 j2b1b2 a1a2 b1b2 j a1b2 a2b1 .

z1

a1 jb1

a

ib

∙│∙

умножим

и

разделим

на сопряженный

z

2

2

2

знаменатель ∙│∙ =

1*

a1 b1

a2 b2

a1a2 b1b2 j a2b1 a1b2

a a b b

j

a b a b

.

a2 b2

a2 b2

a22 b22

a22

b22

a22

b22

1

2

1

2

2

1

1

2

Возведение в степень. Если z

z

e j

z

cos j sin , то

zn

z

n e jn

z

n cos n j sin n .

Извлечение

корня

n –

ой

степени.

Если

z

z

e j

z

cos j sin , то

n z n

z

e j n

z

e

j

2kπ

n

z

2kπ

i sin

2kπ

, где

n

cos

n

n

k0,1,...,n 1.

Здесь и в дальнейшем знаки ∙│∙ ∙│∙обозначают скобки, в которых даны пояснения.

7

1.1.2. Элементы линейной алгебры

– матрицы и определители

Прямоугольные таблицы вида

а11

а12

...

а1n

а

а

а

21

а

22

...

а

2n

11

12

,

.......

,

,

а21

.aij ..

а22

... ...

...

аm1

аm2

...

аmn

имеющие m

строк и

n

столбцов

и

состоящие

из

элементов aij

i 1,2,..., m; j 1,2,..., n , называются матрицами. Элементами матриц

могут быть числа, функции или элементы иной природы. Элемент aij находится на пересечении i той строки и j того столбца.

Обозначаются матрицы большими буквами A,B,C,…,а также

aij , bij mn ,aij mn .

При m=n – матрица квадратная, при m≠n – прямоугольная.
Матрицу aij 1n	a11a12...a1n называют матрицей-строкой.
	b
Матрицу bij m1	11
	b21		называют матрицей-столбцом.
	b
	m1

Этими матрицами выражают вектора, количество координат которых равно количеству элементов матрицы.

Определителем 2-ого порядка, соответствующим матрице

à11

à12

, называется число |А| =

a

a

a

a

a

a .

А =

11

12

22

21

à21

a21

a22

11

12

à22

Определителем 3-его порядка, соответствующим квадратной

a	a	a
11	12	13
матрице А= a21	a22	a23		называется число
	a32	a33
a31

			a11	a12	a13
A			a21	a22	a23	a11a22a33 a12a23a31 a21a13a32
			a31	a32	a33

8

a31a22a13 a21a12a33 a11a32a23 a11

a22

a23

a12

a21

a23

a13

a21

a22

.

a a

a a

a a

32

33

31

33

31

32

Минором Мij элемента аij называется определитель, полученный из данного определителя вычеркиванием i - строки и j- столбца.

Так, минором М23 определителя 3-его порядка является определитель, получаемый вычеркиванием второй строки и третьего

столбца из исходного определителя:	М23=		a11	a12		.
			a31	a32
Алгебраическим дополнением Аij	элемента			аij определителя
называется определитель, равный Аij = (-1)i+j Мij.

Вычисление определителя по элементам строки или столбца.

Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения:

n

n

A

aij Aij

aij Aij

i 1

j 1

Так, по элементам второй строки вычислим определитель 3-его

порядка:

a11

a12

a13

3

a21

a22

a23

|А| =

a2 j A2 j

a31

a32

a33

j 1

a21

1 2 1

a12

a13

a22

1 2 2

a11

a13

a23

1 2 3

a11

a12

.

a32

a33

a31

a33

a31

a32

Операции над матрицами.

Суммой двух матриц А = (аij) и В = (bij), имеющих одинаковый

размер, называется матрица С =(сij), каждый элемент которой равен сумме соответствующих элементов матриц А и В.

сij= аij+bij ; i =1,2, … , m, j =1,2, … , n.

Произведением матрицы А = (аij) на число λ называется матрица λА=( λ аij ), где каждый элемент матрицы А умножается на число λ.

Произведением матрицы А = (аij)mp на матрицу В = (bij)pn называется матрица С=(сij)mn=AB , элемент сij которой равен сумме

произведений соответствующих элементов i -ой строки матрицы А и j -ого столбца матрицы В:

9

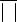
p

cij aik bkj ai1b1 j ai2 b2 j aik bkj aipbpj. k 1

Произведение матриц имеет смысл только в случае, когда число столбцов матрицы A равно числу строк матрицы B.

Так, например,

	1	2			3		1	2			1 3 2 5				1 1 2 0	1 2	2	1		13		1	4
																									.
	3	4
						5	0	1				3	3	4 5	3 1 4 0						29	3	10
																3 2 4 1

Частный случай скалярное произведение векторов:

				b
a a		a			1		a b	a	b	a b .
	2		3		b
1					2		1 1		2 2	3 3
				b
					3

Квадратная	матрица А называется вырожденной, если ее
определитель |А| = 0,		и невырожденной , если	|А| ≠ 0.
Обратной	для	невырожденной матрицы	А называется
матрица А-1 такая, что

A A 1 A 1 A E ,

где Е – единичная матрица (по главной диагонали которой стоят единицы, а остальные элементы равны 0).

Чаще всего обратную матрицу A-1 находят по формуле:

A 1 1A Aij T , где

Aij матрица, составленная из алгебраических дополнений исходной матрицы A aij . Значок «Т» обозначает транспонирование:

строки и столбцы матрицы меняются местами.

Так, обратная матрица А-1 для квадратной матрицы А 3-его порядка имеет вид :

a

22

a

23

a

a

a

a

12

13

12

13

A11

A21

A31

a

32

a

33

a

32

a

33

a

22

a

23

1

1

a21

a23

a11

a13

a11

a13

1

A

A12

A22

A32

.

A

a11

a12

a13

a31

a33

a31

a33

a21

a23

A

A

A

13

23

33

a

a

a

a

21

a

22

a

a

a

a

21

22

23

11

12

11

12

a31

a32

a33

a31

a32

a31

a32

a21

a22

1.1.3. Методы решения систем линейных алгебраических уравнений (СЛАУ)

Рассмотрим систему трех линейных алгебраических уравнений

10