Федеральное агентство по образованию

ГОУ ВПО «Уральский государственный технический университет – УПИ»

Дифференциальные уравнения

Методические указания к заданиям и варианты индивидуальных домашних заданий для студентов всех форм обучения

Екатеринбург

2005

УДК 5.17

Составители В.Б.Грахов, В.В.Катальников, В.П.Кочнев

Научный редактор проф., канд. физ.-мат. наук В.А.Табуева

Дифференциальные уравнения: Методические указания к заданиям и варианты индивидуальных домашних заданий / В.Б.Грахов, В.В.Катальников, В.П.Кочнев. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. 50 с.

В настоящих методических указаниях представлены основные понятия и методы решения дифференциальных уравнений, а также варианты домашних заданий, охватывающих все основные разделы теории обыкновенных дифференциальных уравнений.

В качестве примера разбираются решения типовых задач.

Методические указания предназначены для студентов I курса всех форм обучения всех специальностей УГТУ-УПИ.

Библиогр.: 5 назв.

Подготовлено кафедрой «Вычислительные методы и уравнения математической физики».

© ГОУ ВПО «Уральский государственный

Технический университет – упи», 2005

Введение Основные понятия

Уравнение называется дифференциальным относительно некоторой искомой функции, если оно содержит хотя бы одну производную этой функции. Порядок дифференциального уравнения совпадает с порядком наивысшей производной, входящей в это уравнение.

Если искомая функция является функцией одного аргумента , то дифференциальное уравнение называется обыкновенным. Например, уравнение где является обыкновенным дифференциальным уравнением первого порядка. (В дальнейшем для краткости слово «обыкновенное» будем опускать.)

В общем случае дифференциальное уравнение (ДУ) n-го порядка может быть записано в виде

(1)

Если удаётся его разрешить относительно старшей производной, то получаем уравнение в нормальной форме

(2)

Процесс нахождения решений дифференциального уравнения называется интегрированием уравнения.

Решением (или интегралом) дифференциального уравнения называется такая дифференцируемая функция у =у(х), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество.

Если функция, являющаяся решением дифференциального уравнения, определена в неявном виде: то называется интегралом данного дифференциального уравнения.

Общим решением дифференциального уравнения (1) или (2) называется функция вида , удовлетворяющая следующим двум условиям:

1) оно является решением уравнения (1) или (2) при любых значениях , ;

2) для любых начальных данных при которых дифференциальное уравнение имеет решение, можно указать значения постоянных C_i=C_i0 , при которых будут выполнены начальные условия

(3)

Всякое решение уравнения получающееся из общего решения при конкретных значениях называется частным решением.

Задача, в которой требуется найти частное решение уравнения (1) или (2), удовлетворяющее начальным условиям называется начальной задачей Коши, или просто задачей Коши.

График решения (или интеграла) дифференциального уравнения (1) или (2) на плоскости Оху называется интегральной линией. Следовательно, каждому решению или интегралу соответствует интегральная линия.

Если правая часть уравнения (2) является непрерывной функцией и имеет непрерывную производную в области D , то решение уравнения (2) в этой области при начальных условиях (3) существует и единственно, то- есть через точку (х₀, у₀) проходит единственная интегральная кривая данного уравнения (т е о р е м а К о ш и).

Линейные дифференциальные уравнения высшего порядка

Линейным неоднородным дифференциальным уравнением (ЛНДУ) второго порядка называется уравнение вида

(4)

где функции непрерывны на некотором отрезке

Функции у₁(х) и у₂(х) называются линейно зависимыми на отрезке , если существуют постоянные числа С₁ и С₂, не все равные нулю, такие, что выполняется условие

. (5)

Если же тождество (5) выполняется только в случае, когда , то функции у₁(х) и у₂(х) называются линейно независимыми.

О линейной зависимости или независимости функций у₁(х) и у₂(х) можно судить по определителю

,

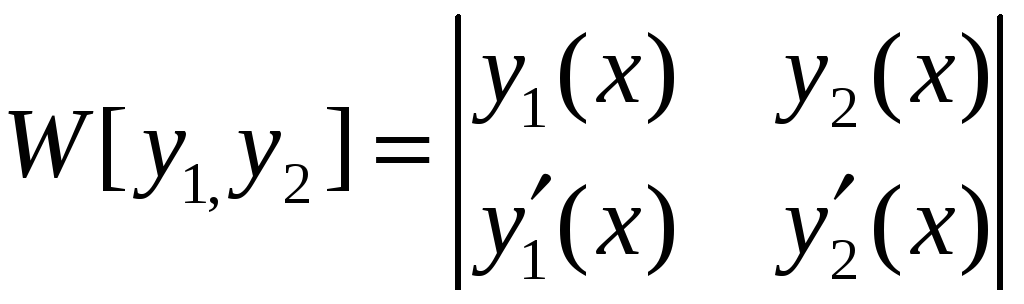который называется определителем Вронского (или просто вронскианом)

Теорема 1. Если функции у₁(х) и у₂(х) линейно зависимы на отрезке , то для всех х из .

Теорема 2. Если у₁(х) и у₂(х) линейно независимые на отрезке решения дифференциального уравнения (4), то определитель Вронского этих функций отличен от нуля во всех точках отрезка .

На основе этих теорем строится общее решение линейного дифференциального уравнения.

Теорема 3. Общее решение у_оо линейного однородного дифференциального уравнения (ЛОДУ) (5) имеет вид

где - линейно независимые решения этого уравнения.

Таким образом, для того чтобы получить общее решение однородного уравнения (5), достаточно найти любые два линейно независимых частных решения этого уравнения. В этом случае говорят, что они образуют фундаментальную систему решений (ФСР) уравнения (5).

Теорема 4. Общее решение у_он линейного неоднородного дифференциального уравнения (ЛНДУ) (4) представляется в виде суммы

где у_оо – общее решение соответствующего однородного уравне - ния (5), а у_ч – некоторое частное решение неоднородного уравне­­- ния (4).

Проще всего задача нахождения общего решения решается, если коэффициенты p(x) и q(x) в уравнении (4) не зависят от х.

Рассмотрим ЛОДУ второго порядка с постоянными коэффициентами

(6)

Фундаментальную систему решений этого уравнения можно найти следующим образом. Составляем алгебраическое уравнение

r² + pr + q = 0, (7)

которое называется характеристическим уравнением для уравне-ния (6).

Для составления общего решения у_оо дифференциального уравнения (6) необходимо найти корни r₁ и r₂ соответствующего характеристического уравнения (7) и применить следующую теорему:

Теорема 5. Пусть корни r₁ и r₂ – корни характеристического уравнения для уравнения (6). Тогда общее решение уравнения (6) находится по одной из трёх следующих формул:

1. если r₁ и r₂ – действительные и r₁ ≠ r₂ , то

2. если r₁ = r₂, то

3. если 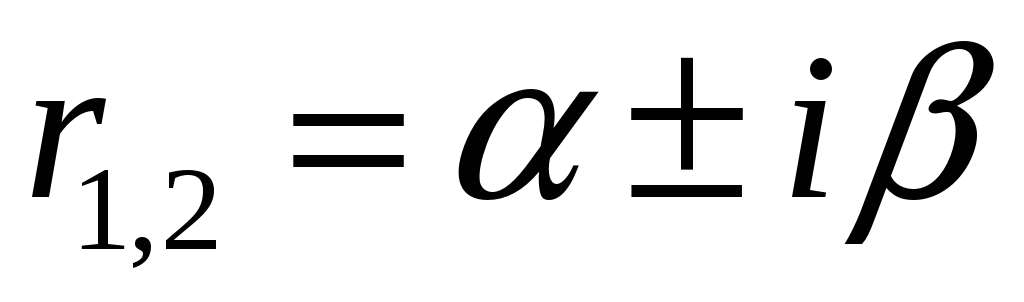- комплексно-сопряжённые корни, то

Чтобы найти общее решение линейного неоднородного уравнения

, (8)

нужно найти его частное решение у_ч. Это легко сделать в случае, когда правая часть имеет специальный вид, и оно находится методом неопределённых коэффициентов.

1. где - многочлен степени n.

а) Если не является корнем уравнения (7), то частное решение ищется в виде

(9)

где - многочлен степени n с неизвестными коэффициентами.

б) Если - корень уравнения (7) кратности k, то частное решение записывается в виде

(10)

Вид этих решений справедлив и при = 0.

2. где P_n(x) и Q_m(x) – многочлены степени n и m соответственно. Положим . Тогда

, (11)

где , если не является корнем уравнения (7), и отлично от нуля, если – корень уравнения (7) кратности k.

Частное решение ЛНДУ (8) в случае специального вида f(x) и в общем случае можно найти методом вариации произвольных постоянных (метод Лагранжа). Суть его в следующем. Если y₁(x) и y₂(x) – фундаментальная система решений ОЛДУ (6), тогда частное решение можно представить в виде где функции C₁(x) и C₂(x) находятся из системы дифференциальных уравнений

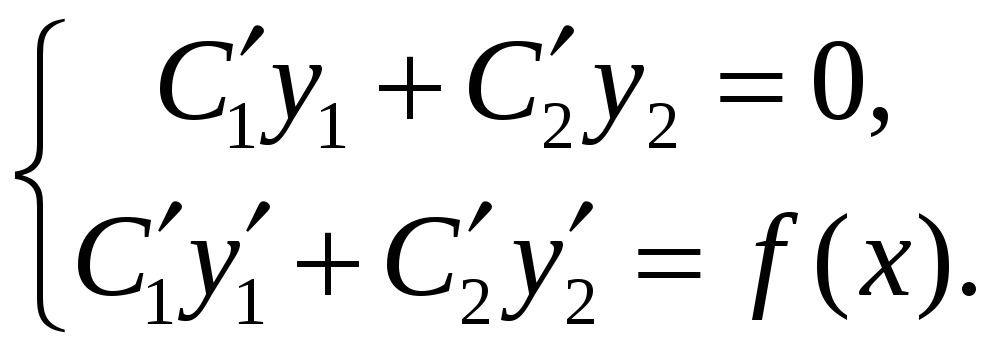
Ниже приводятся примеры решения дифференциальных уравнений, аналогичных в заданиях.