
- •Глава 3. Производная функции одной переменной
- •3.1. Производная функции в точке
- •X Физический смысл производной
- •Геометрический смысл производной. Связь с существованием касательной
- •Уравнения касательной и нормали
- •Бесконечные производные
- •Односторонние производные
- •3.2. Дифференцируемость функции одной переменной Определение функции, дифференцируемой в точке
- •Теорема 3.3 (необходимое и достаточное условие дифференцируемости)
- •Теорема 3.4 (о непрерывности дифференцируемой функции в точке)
- •3.3. Правила вычисления производных
- •3.6. Производные некоторых элементарных функций (таблица производных)
- •3.7. Логарифмическая производная
- •3.8. Производная функции, заданной параметрически
- •3.9. Дифференцирование функций, заданных неявно
- •Глава 4. Производные и дифференциалы высших порядков
- •4.1. Дифференциал функции одной переменной
- •Геометрический смысл дифференциала
- •Инвариантность формы дифференциала первого порядка
- •Дифференциал и приближенные вычисления
- •4.2. Производные и дифференциалы высших порядков Понятие производной - го порядка
- •Дифференциалы высших порядков
- •Правила вычисления производной суммы - го порядка. Формула Лейбница для- й производной произведения двух функций
- •4.3. Теоремы о непрерывных и дифференцируемых функциях
- •4.4. Формулы конечных приращений, их приложения
- •Теорема Ролля5о среднем
- •4.5. Раскрытие неопределенностей (Правило Лопиталя)
- •4.6. Формула Тейлора для многочленов
- •4.7. Задача наилучшего локального приближения. Формула Тейлора с остаточным членом в форме Пеано10
- •4.8. Формула Тейлора с остаточным членом в форме Лагранжа
- •Формула Маклорена11
- •4.9. Разложения основных элементарных функций (асимптотические формулы)
- •Глава 5. Исследование и построение графиков функции одной переменной
- •5.1. Условия возрастания и убывания функции
- •5.2. Локальный экстремум Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
- •5.3. Абсолютный экстремум функции
- •5.4. Выпуклость и точки перегиба графика функции
- •Точки перегиба графика функции
- •5.5. Асимптоты графика функции
- •5.6. Схема исследования функций и построения кривых
УДК 517.1
Составители: О.Я. Шевалдина
Научный редактор: канд. физ.-мат. наук В.И. Максимов
Задачи экономики в курсе математического анализа: Методические указания по курсу «Математика», «Математический анализ» для студентов экономических / О.Я. Шевалдина. Екатеринбург: ГОУ ВПО «УГТУ – УПИ», 2008. 34 с.
Методические указания содержат кратко изложенный теоретический материал, типовые задачи, рекомендации к их решению по теме «Исследование функций с помощью производных. Приложение производной в экономической теории» курса «Математика». Приводятся простейшие приложения математики в экономике (предельный анализ, эластичность функций, максимизация прибыли, оптимизация налогообложения предприятий и др.). Предлагаются задачи для самостоятельной работы студентов (в том числе, с экономическим содержанием). Наряду с традиционными упражнениями приводятся тестовые задания открытой и закрытой формы. Теоретические сведения, а также набор предлагаемых задач можно использовать в процессе аудиторной и самостоятельной работы студентов, при проведении контрольных работ, собеседований и экзаменов. Методические указания предназначаются для студентов всех специальностей факультета экономики и управления.
Подготовлено кафедрой «Анализ систем и принятия решений»
ГОУ ВПО «Уральский государственный
технический университет – УПИ» , 2008
Глава 3. Производная функции одной переменной
3.1. Производная функции в точке
Пусть
функция
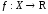 определена на множестве
определена на множестве
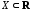 и
и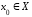 – предельная
точка множества Х.
Напомним: для любой точки
– предельная
точка множества Х.
Напомним: для любой точки
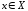 приращение
приращение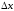 определяется формулой
определяется формулой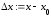 .Приращением
функции
.Приращением
функции
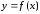 в точке
в точке называется функция аргумента
называется функция аргумента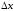 :
:
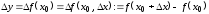 .
.
Определение. Если существует конечный предел
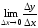 ,
,
то
значение этого предела называют
производной
функции
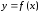 в точке
в точке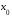 ,
обозначают
,
обозначают
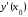 или
или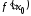 .
.
Используются и другие символические обозначения производной:
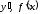 ,
,  ,
,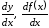 .
.
Лагранж1Ньютон2Лейбниц3
Таким образом, по определению
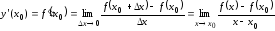 , (3.1)
, (3.1)
где
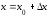 .
.
Пример
3.1. Найдем
производную функции
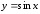 в любой точке
в любой точке области определения:
области определения:
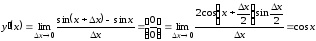 .
.
Следовательно,
функция
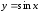 имеет в каждой точке
имеет в каждой точке производную
производную .
.
Экономисты
используют для обозначения производной
также символ
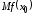 (т. е.
(т. е.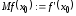 )
и терминмаржинальное
значение функции в точке
)
и терминмаржинальное
значение функции в точке
 .
.
X Физический смысл производной
Производная
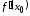 – скорость
изменения функции в точке
– скорость
изменения функции в точке
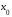 .
В частности, если
.
В частности, если – время,
– время,
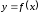 – координата
точки, движущейся по прямой в момент
– координата
точки, движущейся по прямой в момент
 ,
то
,
то – мгновенная
скорость точки в момент времени
– мгновенная
скорость точки в момент времени
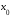 .
.
Геометрический смысл производной. Связь с существованием касательной
Пусть
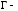 график
функции
график
функции
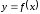 ;
;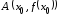 ,
,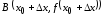 – две точки графика функции
– две точки графика функции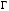 (рис. 3.1).
(рис. 3.1).
Угол
между секущей АВ
и осью Ох
обозначим
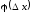 .
.
Г
Определение.
Если существует
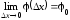 ,
то прямая
,
то прямая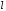 с угловым коэффициентом
с угловым коэффициентом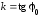 ,
проходящая через точку
,
проходящая через точку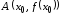 ,
называетсякасательной
к графику функции
,
называетсякасательной
к графику функции
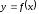 в точке
в точке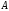 .
.
Теорема
3.1. График
функции
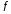 имеет в точке
имеет в точке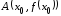 касательную тогда и только тогда, когда
функция
касательную тогда и только тогда, когда
функция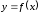 имеет в точке
имеет в точке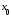 производную
производную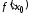 .
.
Доказательство.
Необходимость.
Пусть
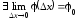 .
Так как функция
.
Так как функция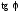 непрерывна, то
непрерывна, то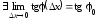 .
Но
.
Но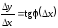 .
Поэтому
.
Поэтому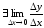 ,
то есть функция
,
то есть функция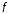 имеет в точке
имеет в точке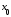 конечную производную
конечную производную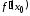 .
.
Достаточность.
Если существует
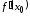 ,
то есть
,
то есть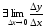 ,
то
,
то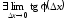 .
Так как функции
.
Так как функции ,
,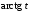 непрерывные, то
непрерывные, то ,
то есть существует касательная к графику
функции в точке
,
то есть существует касательная к графику
функции в точке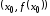 .
.
Замечание.
Так как
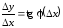 ,
то при
,
то при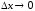 получаем
получаем .
.
Таким
образом,
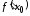 – это тангенс угла наклона касательной
к графику функции
– это тангенс угла наклона касательной
к графику функции в точке
в точке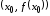 .
.
Уравнения касательной и нормали
Найдем
уравнение касательной. Будем искать
его в виде
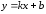 .
Так как
.
Так как ,
то
,
то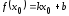 ,
откуда
,
откуда .
Поскольку угловой коэффициент касательной
.
Поскольку угловой коэффициент касательной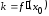 ,
то ее уравнение имеет вид
,
то ее уравнение имеет вид
 .
.
Определение.
Нормальной
прямой (или
нормалью)
к графику
функции
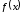 в точке
в точке
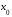 называется прямая, проходящая через
точку
называется прямая, проходящая через
точку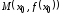 перпендикулярно касательной в этой
точке.
перпендикулярно касательной в этой
точке.
Угловой коэффициент нормали связан с угловым коэффициентом касательной формулой
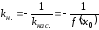 .
.
Уравнение
нормали к графику функции в точке
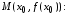
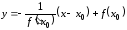 .
.
Бесконечные производные
Если
функция
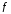 непрерывна
в точке
непрерывна
в точке
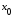 и
и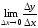 равен
равен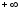 или
или ,
то говорят, что функция
,
то говорят, что функция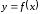 имеет в точке
имеет в точке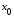 бесконечную
производную
(равную
бесконечную
производную
(равную
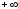 или
или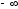 соответственно). В этом случаекасательная
к графику функции
в точке
соответственно). В этом случаекасательная
к графику функции
в точке
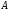 параллельна оси
параллельна оси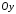 (
(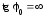 ),
и так как она проходит через точку
),
и так как она проходит через точку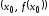 ,
то ее уравнение имеет вид:
,
то ее уравнение имеет вид: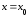 .
.
Пример
3.2. Рассмотрим
функцию
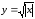 ,
,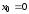 .
Имеем
.
Имеем
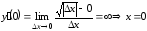 –вертикальная
касательная к графику функции (рис.
3.2).
–вертикальная
касательная к графику функции (рис.
3.2). 
Пример
3.3. Рассмотрим
функцию
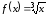 ,
, .
Имеем:
.
Имеем: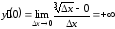 .
Следовательно, прямая
.
Следовательно, прямая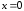 – вертикальная
касательная
к графику функции (рис. 3.3).
– вертикальная
касательная
к графику функции (рис. 3.3). 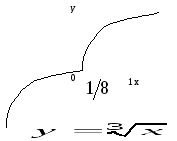
Односторонние производные
Пусть
 определена на множестве
определена на множестве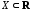 и
и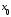 – предельная точка
– предельная точка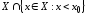
 .
.
Если
существует конечный предел
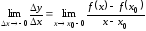 ,
то его называютлевой
производной
функции
,
то его называютлевой
производной
функции
 в точке
в точке
 и обозначают
и обозначают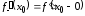 .
.
Аналогично
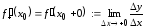 .
Число
.
Число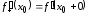 (если оно существует), называетсяправой
производной
функции
(если оно существует), называетсяправой
производной
функции
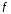 в точке
в точке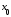 .
.
Теорема
3.2.
Пусть
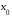 – предельная точка
– предельная точка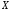 .
Функция
.
Функция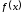 имеет производную в точке
имеет производную в точке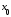 тогда и только тогда, когда
тогда и только тогда, когда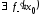 ,
,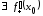 ,
причем
,
причем
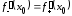 .
.
Пример
3. 4.
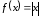 .
.
 .
.
Имеем:
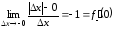 ,
, .
.
Так
как
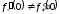 ,
функция
,
функция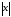 не имеет производной в нуле.
не имеет производной в нуле.
Пример
3.5. Пусть
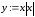 .
Выясним, существует ли производная этой
функции в точке
.
Выясним, существует ли производная этой
функции в точке .
.
Имеем:
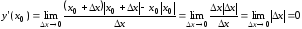 .
.
Итак,
функция
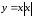 в точке
в точке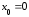 имеет
производную
имеет
производную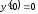 .
.
Пример
3.6.

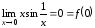 ,
то есть
,
то есть
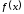 непрерывна в точке
непрерывна в точке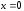 .
Однако
.
Однако
 не
существует. Действительно, если
не
существует. Действительно, если
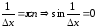 ,
а если
,
а если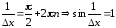 .
Следовательно, предел по Гейне не
существует.
.
Следовательно, предел по Гейне не
существует.
